Mo活化NH3的自旋禁阻反應機理

劉玲玲王永成張 力

(1蘭州城市學院化學與環境科學學院，蘭州 730070)

(2西北師范大學化學化工學院，蘭州 730070)

Mo活化NH3的自旋禁阻反應機理

劉玲玲1王永成＊,2張 力1

(1蘭州城市學院化學與環境科學學院，蘭州 730070)

(2西北師范大學化學化工學院，蘭州 730070)

采用密度泛函理論的UB3LYP方法，計算研究了氣相中Mo活化NH3的反應機理。為了理解由Mo活化NH3過程中自旋翻轉行為，對自旋態分別為七、五、三和單等4個反應勢能面進行了計算研究，其結果表明，Mo活化NH3的過程是通過各自旋態勢能面交叉產生的典型的自旋禁阻反應，最低能量交叉點(MECPs)附近的系間竄越導致2步H轉移和脫H2反應能壘降低。此外運用自然鍵(NBO)軌道理論分析了反應中較為重要的幾個物種的成鍵特性。通過計算在最低能量交叉點(MECPs)附近不同自旋態之間的自旋-軌道耦合常數，再運用Landau-Zener躍遷幾率公式估算了MECPs處系間竄越幾率。所確定的最低能量反應路徑為：7Mo+NH3→7IM1→7/5MECP1→5TS12→5IM2→5/3MECP2→3TS23→3IM3→3TS34→3IM4→3HMoN+H2。

Mo活化NH3；自旋禁阻反應；最低能量交叉點；自旋-軌道耦合；系間竄越幾率

過渡金屬原子或離子對胺類分子N-H鍵的活化在催化反應機理研究中具有重要意義，多年來，探索過渡金屬原子或離子活化C-H、N-H鍵的機理一直是理論化學和實驗化學家研究的熱點之一[1-15]。其中過渡金屬離子活化C-H、N-H鍵的機理研究較多，而過渡金屬原子活化氨分子N-H鍵的機理研究報道尚少[11,14]。近期王雪峰等用激光燒蝕(laser-ablated)實驗方法研究了氣相中Cr、Mo和W原子活化NH3分子的反應[15]，用FTIR譜檢測了反應過程的中間體和產物，并對中間體和最終產物在特定的自旋態下進行了理論計算驗證。實驗結果表明，在Mo與NH3的反應中有HMoN產物生成，并伴隨有H2放出。

眾所周知，過渡金屬Mo原子的d軌道未充滿電子，其基態應為高自旋態。當它與NH3反應時，由于d電子在反應體系內重新調整，中間體和產物分子基態極有可能變為低自旋態，也就是說從反應開始到最終產物，反應體系很可能要經歷多個不同自旋態的反應勢能面。為了能更深入地理解Mo與NH3反應的微觀機理，本文采用密度泛函理論(DFT)中的UB3LYP方法，在多個自旋態勢能面上對Mo與NH3的反應機理進行了計算研究。

1 計算方法

本文對Mo采用含相對論校正的贗勢基組(SDD),N、H 采用 6-311++G(3d，3p)基組,運用密度泛函中的UB3LYP方法,分別對反應體系的單、三、五和七重態的4個反應勢能面上的所有反應物、產物、中間體和過渡態的構型進行了全參數優化,并通過頻率分析,證實了各反應物、中間體和產物的能量是局部極小,各過渡態的構型都有惟一振動虛頻，每一鞍點均通過內稟反應坐標(IRC)計算驗證,證實了反應坐標從鞍點分別走向反應物和產物。

首先根據所計算七、五、三和單重態4個勢能面上反應物、中間體、過渡態和產物的相對能量高低，初步估計不同自旋態勢能面發生交叉的大致位置，用Yoshizawa等的內稟反應坐標垂直激發單點計算方法[16],估算出不同自旋態透熱勢能面(diabatic surface)之間的交叉點(crossing point，CP)，再用Harvey方法[17]優化得到最低能量交叉點(minimum energy crossing point,MECP)的構型和能量 EMECP，最后確定反應體系最低能量反應路徑。

由于最低能量反應路徑可能涉及到多個不同自旋態勢能面的交叉，整個反應可能屬自旋禁阻反應。于是，在勢能面交叉處反應體系由一自旋態勢能面竄越到另一自旋態勢能面的非絕熱過程是此類自旋禁阻反應機理的關鍵所在，也是本文研究的重點之一。根據非絕熱理論[18]，不同自旋態勢能面交叉點處發生系間竄越的難易程度在很大程度上取決于交叉點處2個不同自旋態反應體系的自旋-軌道耦合(spin-orbit coupling，SOC)作用大小。為此，本文運用GAMESS程序，選擇合適的活性軌道空間，計算了最低能量交叉點(MECP)處不同自旋態的自旋-軌道耦合常數，并運用Landau-Zener躍遷幾率公式估算了MECP處的系間竄越幾率。

主要計算工作運用Gaussian03[19]程序包完成，僅用GAMESS程序計算了體系的自旋-軌道耦合作用。

2 結果與討論

2.1 結構及反應路徑的確定

2.1.1 結構優化結果

分別在4個勢能面上優化了33個反應物、中間體(IM)、過渡態(TS)及產物構型，因篇幅所限，僅將在本文中涉及到的和最低能量反應路徑上的物種構型繪于圖1。

頻率分析與文獻[15]結果基本吻合。涉及反應生成N≡MoH和H2相關物種的紅外譜的計算值和實驗觀測值列于表1。由表1可見，本文計算的3N≡MoH中所對應的Mo-H(或N)伸縮振動頻率與實驗觀測值相吻合，1NMoH3與文獻[15]計算值相符。另外，在3NMoH3中Mo-H(H1和H3)的對稱和反對稱伸縮振動頻率較低(666，982 cm-1)，而H1與H3之間伸縮振動頻率很高(3894 cm-1)，說明了這兩個Mo-H鍵較弱，而H-H鍵很強。由此可初步推斷脫氫反應可能發生在3NMoH3物種上，因3NMoH3分解生成了3N≡MoH和 H2，實驗觀測值 1 815、1 081cm-1可能是3N≡MoH與3NMoH3混合物中Mo-H和Mo-N的伸縮振動頻率。

2.1.2 NBO分析及鍵結構分析

為了探討各物種成鍵特征，對處于不同自旋態的反應物、中間體(IM)及產物進行了NBO計算。計算結果表明，同類型物種，自旋態越低，Mo與N之間的成鍵數目越多，這與Mo原子的空d軌道數目密切相關。當Mo與NH3靠近形成反應復合物(IM1)時，4個不同自旋態物種具有相似的構型。1IM1、3IM1和5IM1中Mo與N之間有一個主要由N提供電子對的σ配位鍵，如5IM1：σMo-N=0.341 2(sp0.01d1.21)Mo+0.9400(sp3)N(Mo占 11.64%，N 占 88.36%)。而7IM1中Mo因有6個自旋平行的單電子，沒有空軌道與N成鍵，故在7IM1中Mo與N間的距離最長(0.264 4nm)。在IM2中，除了都有1個Mo-H鍵外，1IM2、3IM2中的Mo、N之間是雙鍵，如3IM2：σMo-N=0.454 9(sd2.14)Mo+0.8905(sp1.57)N(Mo占 20.69%，N 占 79.31%)，πMo-N=0.4701(p1.00d99.99)Mo+0.8826(p1.00)N(Mo占 22.10%，N占77.90%)；5IM2中的 Mo、N之間是單鍵，而7IM2中Mo、N之間仍未成鍵。對于IM3，除了都有2個Mo-H鍵外，所不同的是1IM3的Mo、N之間是三鍵；7IM3中有了1個Mo-N鍵。在IM4中，3IM4中Mo、N之間形成了三鍵；5IM4中的Mo、N之間形成了雙鍵。有趣的是在1IM4有 3個 Mo-H鍵，3IM4、5IM4和7IM4中只有1個Mo-H鍵。且由3IM4、5IM4和7IM4結構可知，1、3號2個H原子間距離分別為0.0773、0.0775、0.0748 nm，已接近氫分子中H原子間的平衡距離 (0.074 nm)，NBO計算結果也證實了2個H原子間已成鍵，如3IM4：σH1-H3=0.7071(s)H1+0.7071(s)H3(H1占50.00%，H3占50.00%)，分子軌道布居分析也支持了H1與H3之間已成鍵的結論。由此推斷，Mo活化NH3的過程中，在三、五和七重態勢能面上都會有放出H2的可能性。

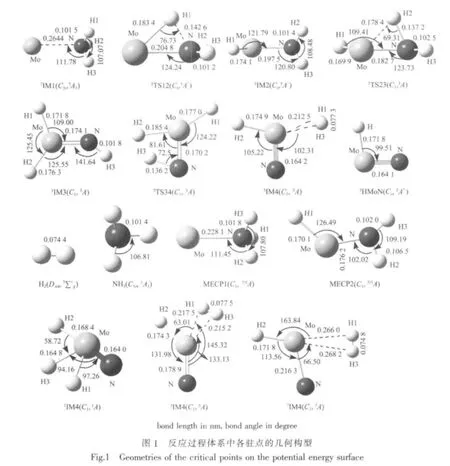
表1 NMoH3和N≡MoH的振動頻率(cm)Table 1 Vibrational frequencies of the NMoH3and3N≡MoH(in cm-1)

2.1.3 低能反應路徑的確定

采用B3LYP所計算Mo原子不同自旋態的能量大小順序均為：7Mo＜5Mo＜3Mo＜1Mo，基態和第一激發態電子組態分別為5s4d5(7S)和5s24d4(5D)，Mo原子第一激發態能量比基態能量高出142.737 kJ·mol-1。用CCSD(T)方法驗證能量大小次序的結果與前一致，為了使計算能量前后一致，文中的能量均為B3LYP方法的計算能量。

Mo活化NH3的4個不同自旋態勢能面反應路徑所涉及的駐點能量見圖2(經零點能校正)。由圖2可見，最低能量反應路徑應是Mo以高自旋態(7S)進入反應通道，與NH3形成能量較低的初始反應復合物7IM1，過程放熱 15.212 kJ·mol-1。從 IM1 到 IM2 是第一個H向Mo轉移的過程。由于7IM2能量很高，七重態勢能面上的反應是強吸熱過程，而在單、三和五重態勢能面上有較低能量的中間體，其中尤以五重態的5IM2能量最低。經用Yoshizawa方法[16]估算，七重態與五重態勢能面在7IM1與5TS12之間發生交叉(交叉點為CP1)，為反應體系從七重態到五重態勢能面提供了一條系間竄越途徑。根據自旋-軌道耦合選擇定則[20]，七重態到五重態總自旋的改變值ΔS=-1，滿足自旋-軌道耦合選擇定則條件(ΔS=±1)，具有在自旋-軌道耦合作用下發生電子自旋翻轉的可能性。從IM1到IM2的過程可能是在CP1處先從七重態勢能面竄越到五重態勢能面上，再翻越五重態能壘(5TS12)到達5IM2，由于5TS12能量比7TS12能量低104.93 kJ·mol-1，所以反應體系經系間竄越到達五重態勢能面后，大大降低了反應能壘，獲得了一條低能反應路徑。七重態勢能面與單、三重態勢能面的交叉處不滿足自旋-軌道耦合選擇定則，自旋-軌道耦合常數為零，本文不予討論。

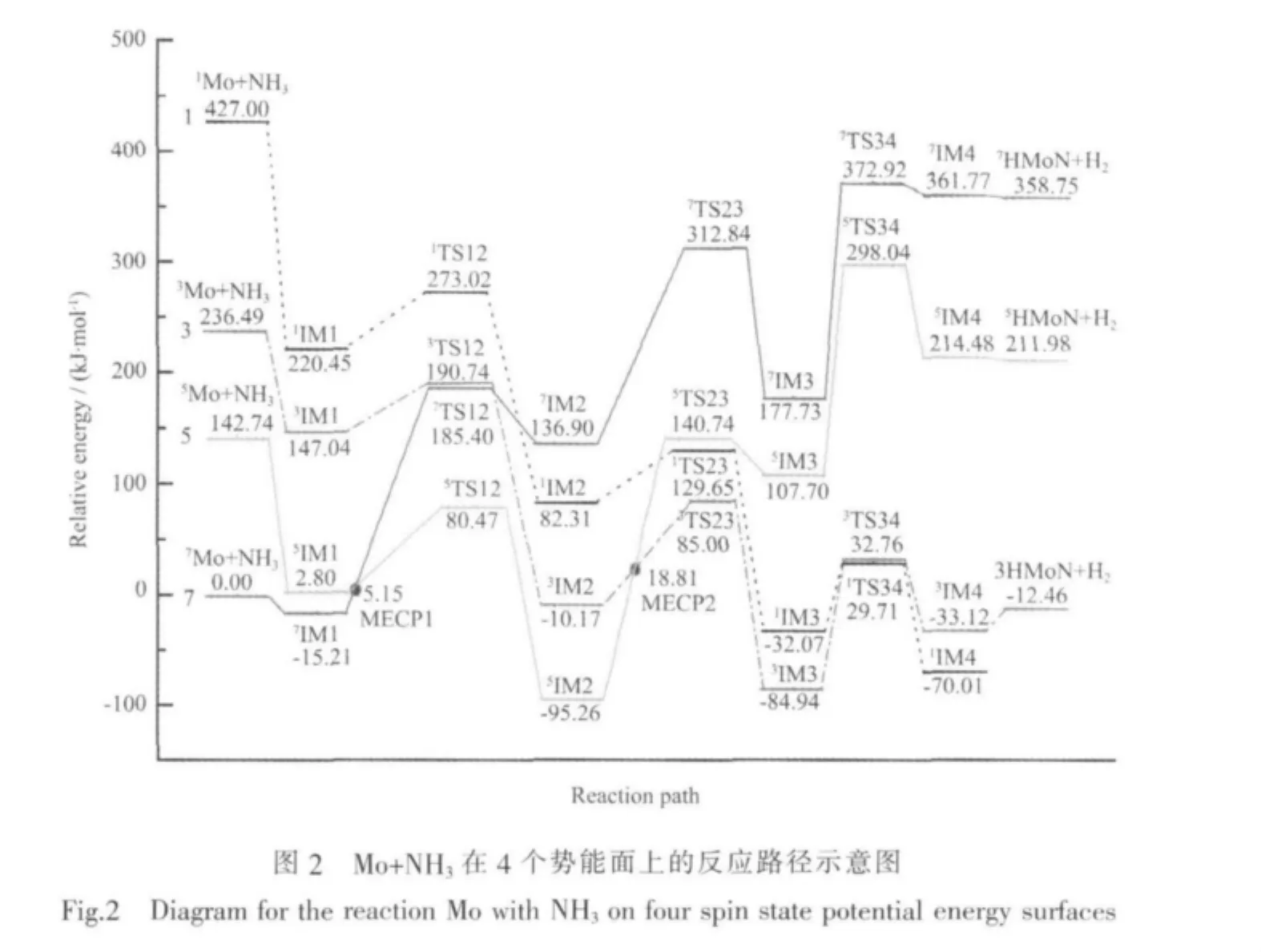
從IM2到IM3是第2個H轉移到Mo上的過程。除在五重態勢能面上的反應表現出強吸熱以外，單態和三重態勢能面上的反應都是強放熱過程，中間體IM3中尤以3IM3能量最低，故第2個H轉移到Mo上的中間產物以三重態3IM3最為穩定。經用Yoshizawa方法[16]做類似估算，在5IM2與3TS23之間也存在五、三重態勢能面的交叉(交叉點為CP2)，根據旋-軌耦合選擇定則，五、三重態勢能面交叉也符合自旋-軌道耦合選擇定則(ΔS=±1)，說明具有在自旋-軌道耦合作用下發生電子自旋翻轉的可能性。從IM2到IM3，由于在交叉點CP2附近有效自旋-軌道耦合作用的促進，反應體系可能經系間竄越到達三重態勢能面上，再翻越三重態勢能面上的第二個過渡態3TS23到達3IM3。由于過渡態3TS23能量比5TS23能量低55.74 kJ·mol-1，所以再一次降低了反應能壘。

從IM3到IM4是N上的第3個H向Mo轉移的過程。在三重態勢能面上的反應是吸熱過程，而在單態勢能面上的反應則是放熱的，產物IM4中1IM4的能量最低，因此1IM4應為最為穩定的產物。然而，由構型優化和IRC計算結果可知，單態和三重態的TS34和IM4構型相差較大，而且H轉移的反應路徑有所不同。雖然說單、三態勢能面交叉能在旋-軌耦合作用下發生有效的系間竄越，但經反復計算核實，未發現三重態與單態勢能面交叉點，這說明由3IM3到1IM4可能沒有系間竄越途徑。有趣的是在單態勢能面上不存在含有H-H成鍵物種，于是可推斷在1IM4中不能放出H2氣。根據文獻[15]報道的實驗事實判斷，較為穩定的3IM3只能沿著三重態勢能面越過3TS34到達3IM4，而在3IM4中H1與H3之間的距離僅有0.0773 nm。另外，分子軌道布居和NBO分析都表明了H1與H3之間已成鍵，3IM4中的(NMoH2)已形成了角形的[N≡Mo-H]鍵構型，并與3NMoH分子相差不大。這些證據充分說明了脫氫反應是在三重態勢能面上完成的，此結論與前面的紅外光譜數據分析結論相一致。

2.2 勢能面交叉點MECP1、MECP2的確定和計算及軌道分析

由于反應體系以七重態進入反應通道，所以選擇七重態從7IM1到7IM2勢能面的內稟反應坐標(7IRC12)，運用Yoshizawa內稟反應坐標垂直激發單點計算方法[16]，計算了7IRC12上諸點構型對應的五重態垂直激發能，這些能量點構成的勢能曲線就是7IRC12在五重態勢能面上的垂直投影，此曲線與7IRC12曲線有交點，即為估算出的CP1點(但不是最低能量交叉點)。然后反應沿著五重態勢能面進行，選擇五重態從5IM2到5IM3勢能面的內稟反應坐標(5IRC23)，運用同樣計算方法，計算了5IRC23上諸點構型對應的三重態垂直激發能，此曲線與5IRC23曲線有交點，即為估算出的CP2點(也不是最低能量交叉點)。最后用同樣方法選擇從3IM3到3IM4勢能面的全部內稟反應坐標(3IRC34)，反復計算了3IRC34上諸點構型對應的單態垂直激發能，此曲線與3IRC34曲線無交點。

因為兩勢能面交叉縫(crossing seam)是3N-7維的超曲面，在交叉縫上必存在能量最低的交叉點(MECP)[17]。為了能準確找到MECP，本文運用由Harvey教授提供的計算MECP的程序，在CP1、CP2構型基礎上優化得到了MECP1和MECP2構型 (均為C1點群，如圖1所示)，相應的能量EMECP1=-124.653613 Hartree、EMECP2=-124.648410 Hartree。為了更進一步驗證MECP1和MECP2位置的可靠性，本文以MECP1為起點，分別在七、五重態勢能面上用最陡下降法(steepest descent)計算了能谷曲線，所計算的七、五重態能谷曲線分別走向了5IM1和7IM1。同樣以MECP2為起點，分別在五、三重態勢能面上用最陡下降法(steepest descent)計算的能谷曲線也分別走向了5IM2和3IM2，于是證實了MECP1和MECP2位置的可靠性。

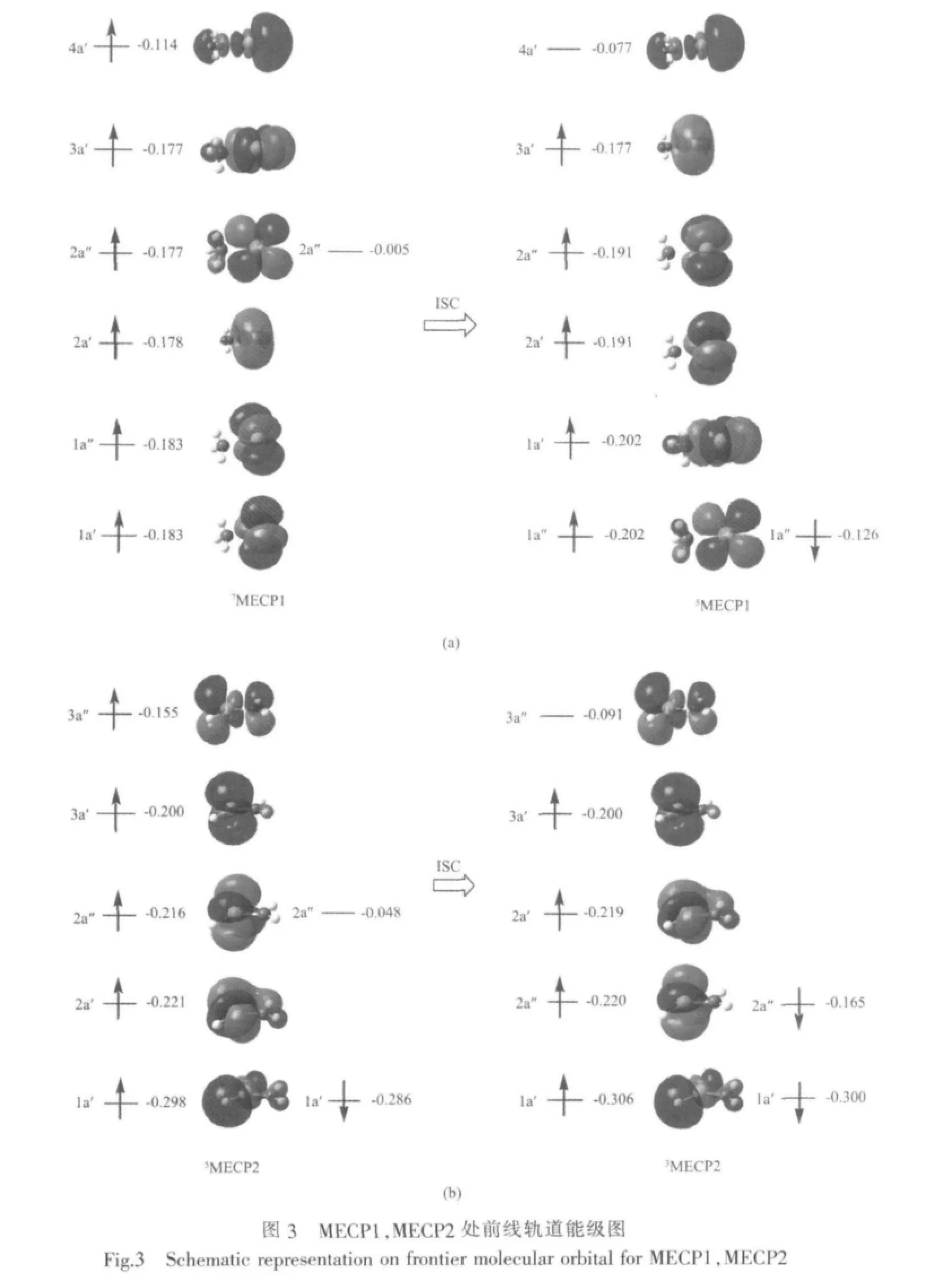
由于反應體系在MECP1點和MECP2點附近電子的自旋態發生了改變，體系的電子組態和前線分子軌道必然會有較大的調整。為了能更深入地了解在MECP附近在系間竄越過程中前線軌道上電子翻轉行為，本文分別對MECP1和MECP2的前線分子軌道進行了計算分析，其結果繪于圖3。從圖3(a)中看出，在MECP1中七重態的最高單占據軌道4a′(屬于Mo-N的σ*反鍵軌道)上的α電子經翻轉為β電子進入到2a″軌道(屬于Mo-N的π*反鍵軌道)上。由于π*反鍵軌道屬雙重簡并，在前線軌道能級次序調整時，Mo-N的2個簡并π*反鍵軌道一并降低了軌道能，3個Mo-N非鍵軌道能同時上升。圖3(b)反映了MECP2處體系在系間竄越前后前線軌道上電子翻轉情況。5MECP2的最高單占據軌道3a″為Mo-N的反鍵軌道，經系間竄越后，其上的α電子經翻轉為β電子進入到2a″軌道(屬于Mo-N的非鍵軌道)上，使得Mo-N的雙占據非鍵軌道2a″能量降低，單占據的非鍵軌道2a′能量同時上升。

2.3 自旋-軌道耦合(SOC)常數和系間竄越幾率PISC的計算

反應體系在MECP1和MECP2處能否發生有效的系間竄越是整個自旋禁阻反應過程的關鍵所在。事實上，在MECP近區2種自旋態之間能量相差很小，電子運動與核運動之間因存在耦合作用而不能分離，使得Born-Oppenheimer絕熱近似失效。在MECP附近反應體系實際是兩種自旋態的混合態，動力學行為十分復雜。理論化學家認為[18,21]，不同自旋態勢能面交叉區發生的電子自旋翻轉是由電子的自旋磁矩與軌道磁矩相互作用的結果，自旋-軌道耦合作用越大，使得電子的自旋翻轉越容易發生，也就是說在MECP附近體系的系間竄越速率主要取決于該處自旋-軌道耦合作用的強弱。

根據單電子近似自旋-軌道耦合Hamiltonian算符定義[20]

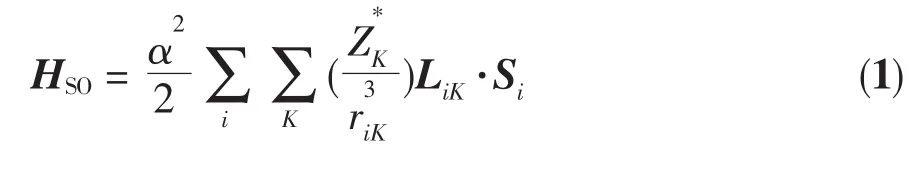
本文選用10個活性軌道的活性空間，運用GAMESS程序計算了MECP1處七、五重態之間和MECP2處五、三重態之間的自旋-軌道耦合常數(耦合非對角元 H12)，其值分別為 216.41 cm-1(MECP1)和20.21 cm-1(MECP2)。計算結果表明，在 MECP1 處七重態與五重態之間具有較大的自旋-軌道耦合常數，由此可推斷反應體系在較強的自旋-軌道耦合作用下，電子較容易發生翻轉，反應體系很容易從七重態勢能面竄越到五重態勢能面上。由于系間竄越速率大小正比于系間竄越幾率PISC。為了能進一步估計MECP1附近系間竄越速率大小，本文采用以下Landau-Zener躍遷幾率公式[22-24]，對單程系間竄越幾率P1ISC和雙程系間竄越幾率P2ISC進行了估算。

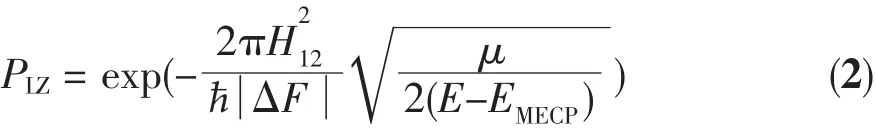
其中H12為不同自旋態的自旋-軌道耦合項，ΔF為MECP1處兩勢能面梯度差，μ為MECP1處在跨越方向上的約化質量，E為相對于反應物的總能量，EMECP為在MECP1處能量。單程系間竄越幾率P1ISC和雙程系間竄越幾率P2ISC(第一次跨越幾率與第二次跨越幾率之和)與Landau-Zene躍遷幾率PLZ之間的關系分別為[22,24]

本文估算的在MECP1處單程系間竄越幾率P1ISC=0.206，雙程系間竄越幾率 P2ISC=0.369，較大的系間竄越幾率說明了在MECP1處的非絕熱反應速率較大，說明該自旋禁阻基元反應過程很容易進行的。

在MECP2處，所計算出的自旋-軌道耦合常數較小(20.21 cm-1)，可能是由于五重態(5ψ)與三重態(3ψ)之間對稱性不匹配的空間軌道較多，減小了自旋-軌道耦合積分值所致。采用 Landau-Zene躍遷幾率公式所估算出的一、二次系間竄越幾率 P1ISC、P2ISC分別為 0.001 和 0.002，說明了此過程的非絕熱程度較大。估算出的一、二次系間竄越幾率很小，只能說明系間竄越速率較小，但在飛秒級非絕熱躍遷速率下，在一定的時間內在MECP2處也有可觀的系間竄越次數[22,25-26]。

3 結 論

通過對Mo與NH3反應機理的計算分析，得出以下結論：(1)反應開始Mo以基態七重態與NH3結合成初始反應復合物Mo(NH3)后進入反應通道，最后以三重態插入產物3N≡MoH和H2離開反應通道，全過程屬自旋禁阻反應。(2)在7IM1-7TS12和5IM1-5TS12之間、5IM2-5TS23和3IM2-3TS23之間分別出現了七重態與五重態、五重態與三重態勢能面之間的交叉，在MECP1處較大的自旋-軌道耦合常數反映了七、五重態勢能面之間具有較強的耦合作用，并具有較大的系間竄越幾率。在MECP2處由于自旋-軌道耦合常數較小而反映出較強的非絕熱性，在一定的時間內也有可觀的非絕熱躍遷幾率。(3)反應體系經過2個交叉點附近的系間竄越，大大降低了整個反應的能壘，為體系在低能反應路徑上進行提供了有利條件。最有利的低能反應路徑為：7Mo+NH3→7IM1→7/5MECP1→5TS12→5IM2→5/3MECP2→3TS23→3IM3→3TS34→3IM4→3NMoH+H2，反應全過程基本不涉及單態勢能面，另外在5/3MECP2和3TS34處可能是非絕熱和絕熱過程的決速步驟。此研究結論對王雪峰的實驗[15]結果給出了較為合理的理論解釋。

致謝：衷心感謝英國Bristol大學Harvey教授為我們免費提供MECP程序!

[1]Szczepanski J,Szczesniak M,Vala M.Chem.Phys.Lett.,1989,162:123-126

[2]Clemmer D E,Sunderlin L S,Armentrout P B.J.Phys.Chem.,1990,94:208-217

[3]Clemmer D E,Sunderlin L S,Armentrout P B.J.Phys.Chem.,1990,94:3008-3015

[4]Clemmer D E,Armentrout P B.J.Phys.Chem.,1991,95:3084-3090

[5]Michelini M C,Russo N,Sicilia E.J.Phys.Chem.A,2002,106:8937-8944

[6]Chiodo S,Kondakova O,Michelini M C,et al.J.Phys.Chem.A,2004,108:1069-1081

[7]Sicilia E,Russo N.J.Am.Chem.Soc.,2002,124:1471-1480

[8]Russo N,Sicilia E.J.Am.Chem.Soc.,2001,123:2588-2596

[9]Chiodo S,Kondakova O,Michelini M C,et al.Inorg.Chem.,2003,42:8773-8782

[10]Chen M,Lu H,Dong J,et al.J.Phys.Chem.A,2002,106:11456-11464

[11]Zhou M F,Chen M H,Zhang L N,et al.J.Phys.Chem.A,2002,106:9017-9023

[12]Blomberg M R A,Siegbahn P E M,Svensson M.Inorg.Chem.,1993,32:4218-4225

[13]Koyanagi K G,Cheng P,Bohme D K.J.Phys.Chem.A,2010,114:241-246

[14]XIE Jun(謝均),QIN Song(秦松),TANG Dian-Yong(唐典勇),et al.Acta Chim.Sin.(Huaxue Xuebao),2010,68(10):969-974

[15]Wang X F,Andrews L.Organometallics,2008,27:4885-4891

[16]Yoshizawa K,Shiota Y,Yamabe T.J.Chem.Phys.,1999,111:538-545

[17]Harvey J N,Aschi M,Schwarz H,et al.Theor.Chem.Acc.,1998,99:95-99

[18]Poli R,Harvey J N.Chem.Soc.Rev.,2003,32:1-8

[19]Frisch M J,Trucks G W,Schegel H B,et al.Gaussian 03,Revision E.01,Gaussian,Inc.,Wallingford CT,2004.

[20]Fedorov D G,Koseki S,Schmidt M W,et al.Int.Rev.Phys.Chem.,2003,22(3):551-592

[21]Schrder D,Shaik S,Schwarz H.Acc.Chem.Res.,2000,33:139-145

[22]Harvey J N.Phys.Chem.Chem.Phys.,2007,9:331-343

[23]Harvey J N,Aschi M.Phys.Chem.Chem.Phys.,1999,1:5555-5563

[24]Harvey J N,Aschi M.Faraday Discuss.,2003,124:129-143

[25]Kim J,Kim T K,Ihee H.J.Phys.Chem.A,2009,113:11382-11389

[26]Zhu Q,Materer N F.Chem.Phys.Lett.,2010,496:270-275

Spin-Forbidden Reaction Mechanism of NH3Activated by Mo Atom in Gas Phase

LIU Ling-Ling1WANG Yong-Cheng＊,2ZHANG Li1
(1College of Chemistry and Environment Science,Lanzhou City University,Lanzhou 730070,China)
(2College of Chemistry and Chemical Engineering,Northwest Normal University,Lanzhou 730070,China)

Gas-phase ammonia activation mechanism by Molybdenum (Mo)atoms was studied at the density functional level of theory using the hybrid exchange correlation functional B3LYP.Four reaction potential energy surfaces(PESs)corresponding to the septet,quintet,triplet,and singlet multiplicities were investigated calculationally in order to understate the presence of some spin inversion during ammonia activation.The results showed that ammonia activation mediated by Mo atoms is a typical spin-forbidden process resulting from the crossing among the multistate PESs.The minimum energy crossing points(MECPs)lead to decrease in the barrier heights of TS12 and TS23 that correspond to the first,second hydrogen transfer and the reductive elimination step of H2,respectively.We also made use of the natural bond orbital(NBO)theory to characterize the bonding characters between different groups for some important species involved.The spin-orbit coupling is calculated between electronic states of different multiplicities at MECPs to estimate the intersystem crossing(ISC)probabilities,and the ISC probability of hopping from one surface to the other in the vicinity of the crossing region is calculated by the Landau-Zener type model.The minimum energy pathway can be described as7Mo+NH3→7IM1→7/5MECP1→5TS12→5IM2→5/3MECP2→3TS23→3IM3→3TS34→3IM4→3HMoN+H2.

NH3activated by Mo;spin-forbidden reaction;minimum energy crossing point;spin-orbital coupling;ISC probability

O643.12

A

1001-4861(2011)03-0519-08

2010-09-14。收修改稿日期：2010-11-25。國家自然科學基金(No.20873102)資助項目。

＊通訊聯系人。E-mail：wangyc@nwnu.edu.cn