對一道高考模擬題的思考

638500 四川省鄰水中學 李真福

在高三教學中，筆者遇到了這樣一道高考模擬題：

其參考答案為∵f'(x)=a-4x3，

本文特記錄筆者對該題目及其參考答案的真實思考過程，以供參考.

1 審題伊始——三個質疑

質疑2參考答案的解法，顯然是認為在閉區間［a，b］上連續，在開區間(a，b)上可導的函數f(x)，其導函數f'(x)的值域(由導數的幾何意義知，它就是切線斜率的取值集合)與f(x)圖象的割線斜率的取值集合一定相等.而實際上，二者并不一定相等.這是因為割線與切線是兩個不同的概念——函數圖象在某點處的切線，是函數圖象在過該點的割線的極限位置，所以二者并不一定相等.例如：

設函數 f(x)=2x3，x∈［-1，1］，

則 f'(x)=6x2，-1＜x＜1，

∴ f'(x)的值域為［0，6)，

由f(x)的圖象(圖1)知，其割線斜率不可能取到0，

∴這時導函數f'(x)的值域與f(x)圖象的割線斜率的取值集合不相等.

下面給出兩個正確結論.

結論1設函數f(x)在閉區間［a，b］上連續，在開區間(a，b)上可導，且函數f(x)圖象的割線斜率的取值集合為M，導函數f'(x)的值域為N，則必有M?N.

這是因為對于函數f(x)圖象的每一條割線，都至少存在一條切線與它平行，所以上述“結論1”正確.

結論2設函數f(x)是在閉區間［a，b］上連續，在開區間(a，b)上可導的凸函數，且函數f(x)圖象的割線斜率的取值集合為M，導函數f'(x)的值域為N，則必有M=N.

這是因為一方面，由上述“結論1”有M?N;而另一方面，由于函數f(x)還是凸函數，所以對于函數f(x)圖象的每一條切線，又都存在至少一條割線與它平行，從而同時有N?M.綜合兩個方面，必有M=N.故上述“結論2”正確.

②將上述“結論2”中的“凸函數f(x)”改為“凹函數f(x)”，其它條件不變，結論仍成立.

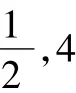
2 另起爐灶——兩種正解

由于該題目的參考答案并沒有證明該題目滿足M=N，所以參考答案提供的解題思路有待商榷.能否換個角度進行求解呢?經過探索，筆者得到了兩種正確解法.

正解1構造函數求解.

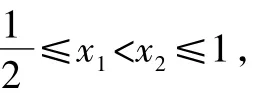
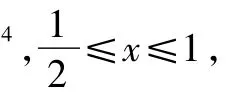
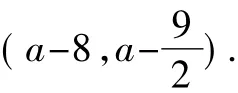
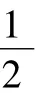
∵由①知，②，③兩式須同時成立，

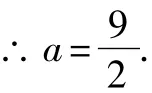
正解2運用不等式的性質求解.

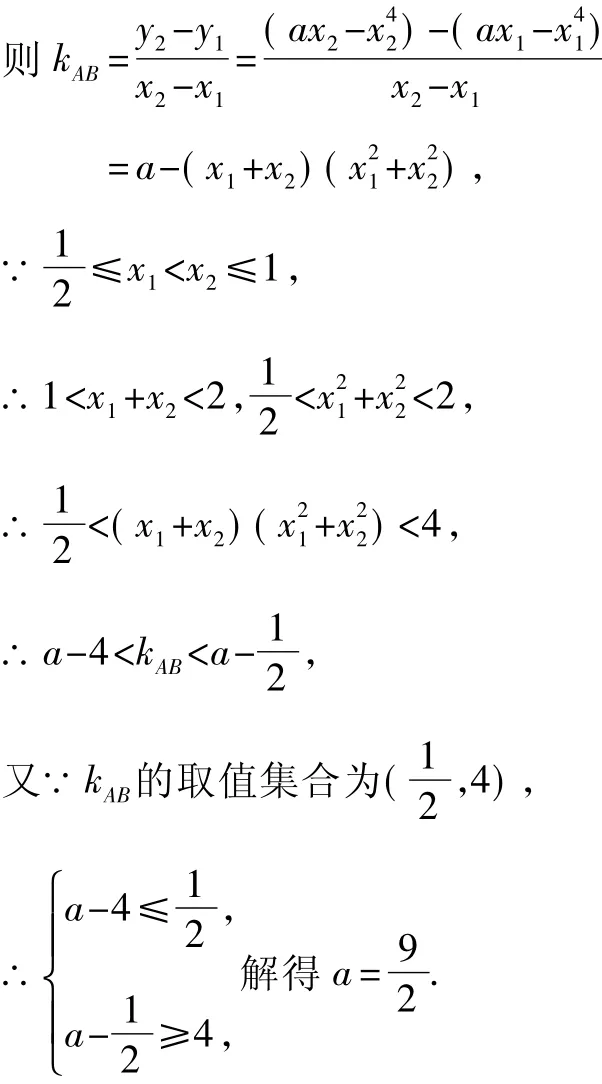
3 揭開面紗——兩點反思

反思1對于在閉區間［a，b］上連續，在開區間(a，b)上可導的函數f(x)，其圖象的割線斜率的取值集合一定是開區間嗎?

反思2參考答案提供的解題思路一定行不通嗎?

經筆者探究，答案也是否定的.請看下面的“正解3”.

∴由上述“結論2”知，f(x)圖象的割線斜率的取值集合M與導函數f'(x)的值域N相等.