一個平面幾何結論的再推廣

●張乃貴 (徐州師范大學2009級教育碩士 江蘇徐州 221000)

結論設P是圓x2+y2=R2上的一點，PA，PB是圓的2條弦，其斜率分別為k1，k2.若k1k2=-1，則弦AB必過圓心(0，0).

文獻［1］對該結論進行推廣得到定理：

定理設P(x0，y0)是圓x2+y2=R2上的一個定點，PA，PB是圓的2條弦，其斜率分別為k1，k2.若k1k2=c(c是常數)，則：

(1)若c=1，則AB的斜率為定值(或不存在);

筆者經過深入研究，將上述定理推廣到橢圓、雙曲線和拋物線中.在利用齊次化方法證明這些性質時，意外發現了一些新的結論，現將之整理成文，與大家交流.

1 在橢圓、雙曲線中的推廣

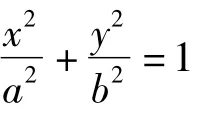
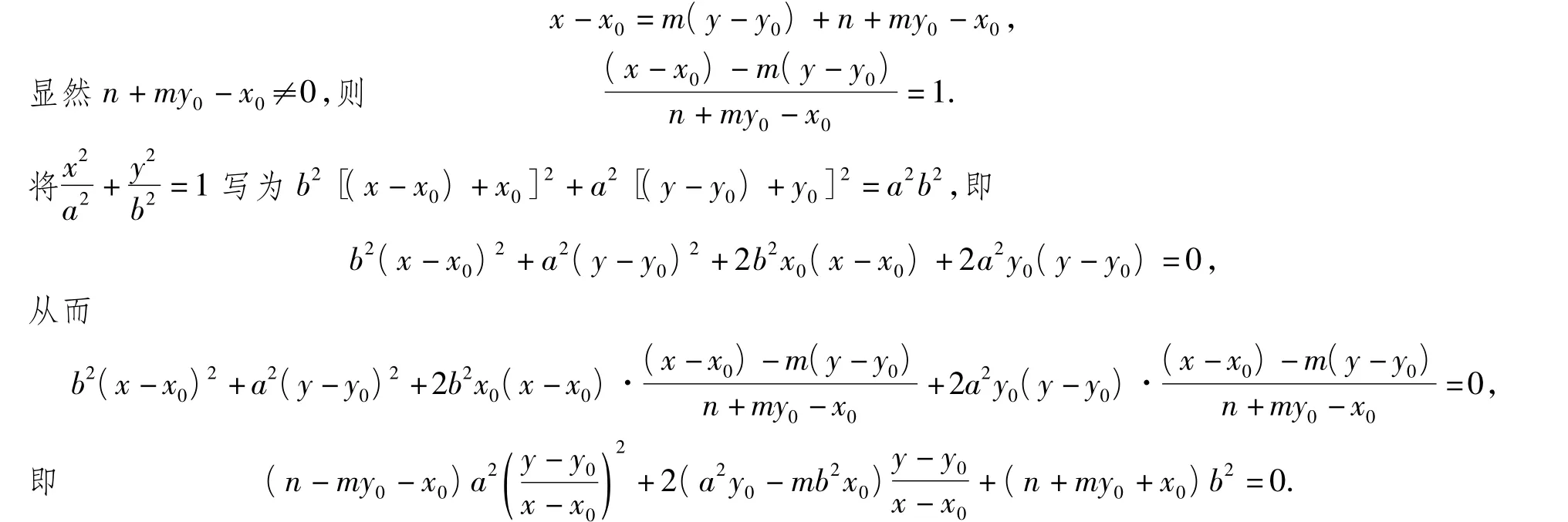
證明設直線AB的方程為x=my+n，即設A(x1，y1)，B(x2，y2)，顯然滿足上述方程，由已知條件及根與系數關系得

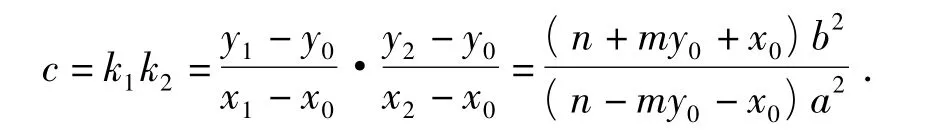
以上利用兩根之積與系數的關系證明了性質1，一種自然延伸的思考是：由兩根之和與系數的關系又能得出什么結論呢?

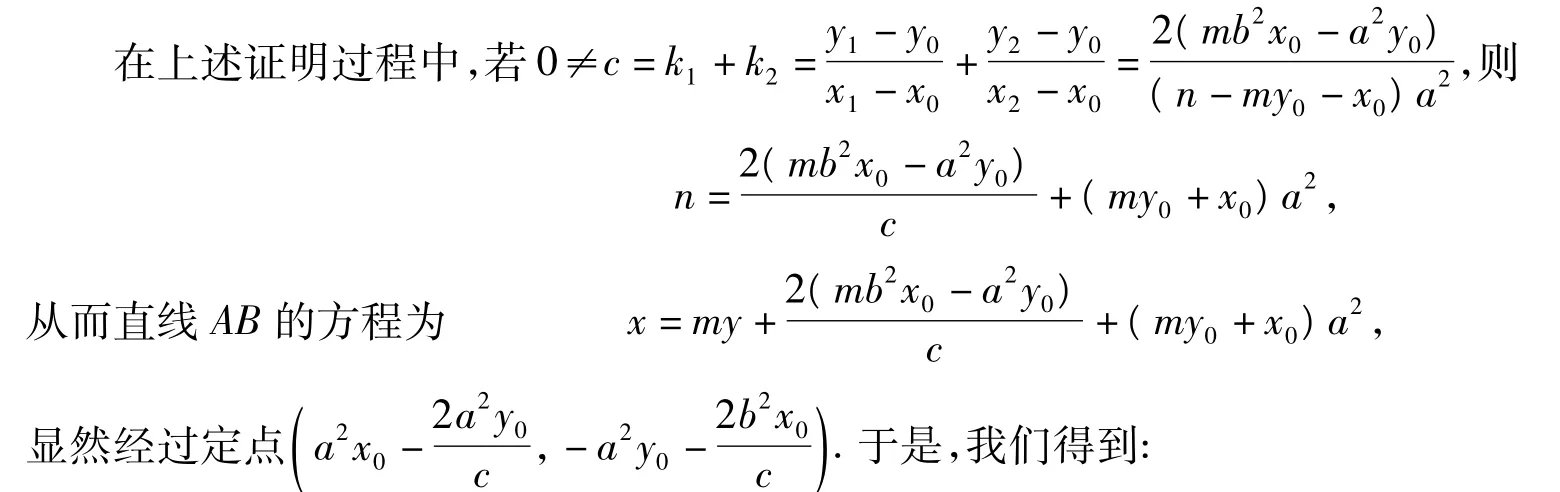
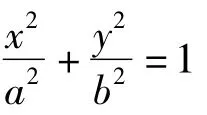
在性質1，2，3中，以-b2代換b2可得到雙曲線中相應的性質.

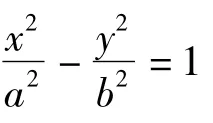
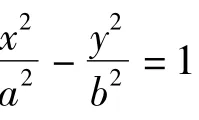
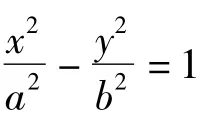
2 在拋物線中的推廣

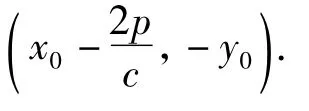
證明設直線AB的方程為x=my+n，即

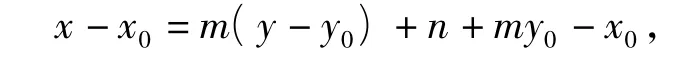
顯然 n+my0-x0≠0，則

將 y2=2px 寫為［(y-y0)+y0］2=2p［(x-x0)+x0］，即

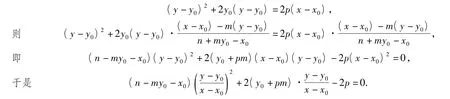
設A(x1，y1)，B(x2，y2)顯然滿足上述方程，由已知條件及根與系數關系得

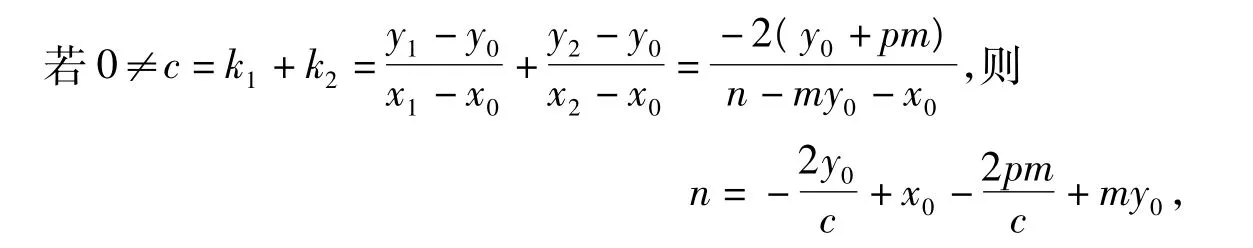
因此我們有：

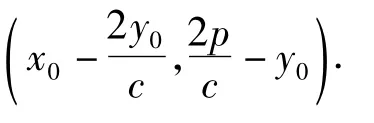
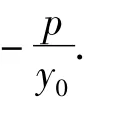
［1］ 徐道.一個平面幾何結論的解析推廣［J］.中學生數學(高中版)，2010(11)：5-6.