以一見多 高效教學

●楊蒼洲 (惠安縣高級中學 福建泉州 362100)

“倡導積極主動、勇于探索的學習方式”是《普通高中數學課程標準》(以下簡稱《新課程標準》)的理念之一.《新課程標準》指出：學生的數學學習活動不應只限于接受、記憶、模仿和練習，高中數學課程還應倡導自主探索、動手實踐、合作交流、閱讀自學等學習數學的方式.因此，在高中數學課堂中，筆者倡導“以一見多，高效教學”.這里的“一”是指為學生構造共同基礎，提供發展平臺，“多”是指注重提高學生的數學思維能力和發展學生的數學應用意識，從而實現高效教學.下面筆者就幾個教學案例談談如何應用“以一見多”的教學方法實現高效教學.

1 一題多解，培養學生的發散性思維

“一題多解”要求學生學會對所給的材料、信息從不同角度、往不同方向、用不同方法或途徑進行分析和解決問題，從而培養學生的發散思維能力.它可以通過縱橫發散，使知識串聯、綜合溝通，達到舉一反三的目的，同時能有效激發學生探索求新的欲望，提高學習數學的興趣.

案例1 已知x2+y2=1，求z=3x+4y的取值范圍.

該案例是筆者在講授人教版高中數學選修4-5“不等式選講”中采用的一個例子.因為當時介紹的是“柯西不等式”的相關內容，所以課堂上師生利用“柯西不等式”共同完成了不等式的證明.

解法1 利用柯西不等式.由

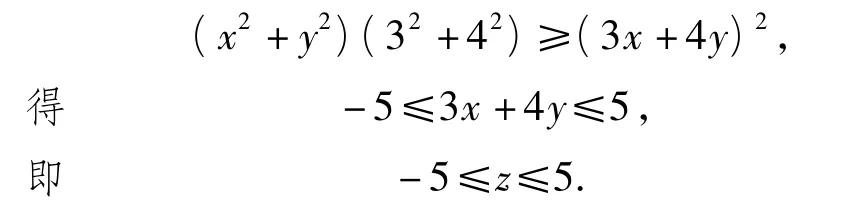
解法2 利用柯西不等式.由

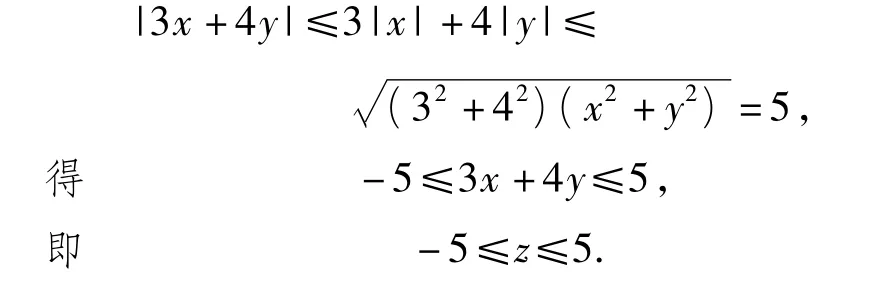
至此，該例題已經完成它作為復習鞏固“柯西不等式”的任務，但為了充分發揮例題的教學功能，培養學生的發散思維能力，提高學生的綜合解題能力，筆者引導學生繼續探究新的解題方法.經過師生的共同努力得到以下幾種解法：

解法3 利用線性規劃.

如圖1所示，首先作直線 l0：3x+4y=0，然后平移l0至位置l1，易得l1的縱截距為，故 z=5.同理，平max移l0至位置l2，易得l2的縱截距為-，故 zmin=-5.

綜上所述，-5≤z≤5.

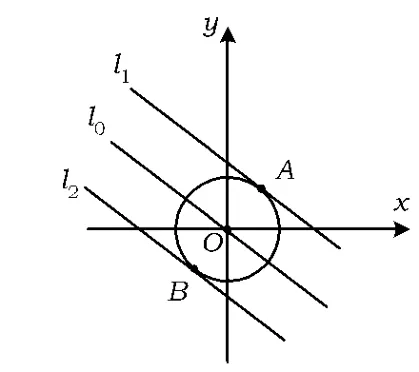
圖1

解法4 利用判別式.

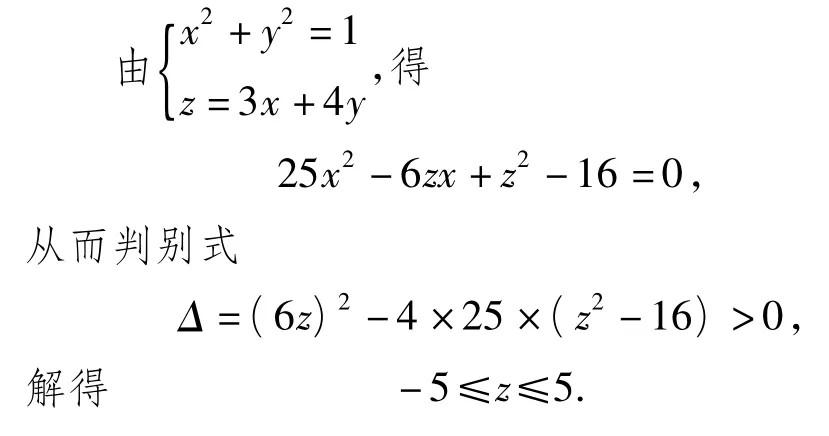
解法5 利用參數.

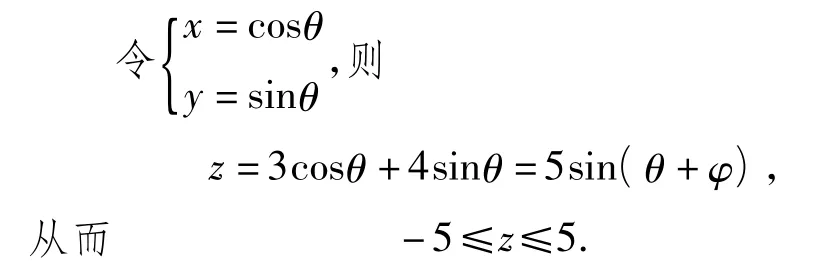
解法6 利用向量法.

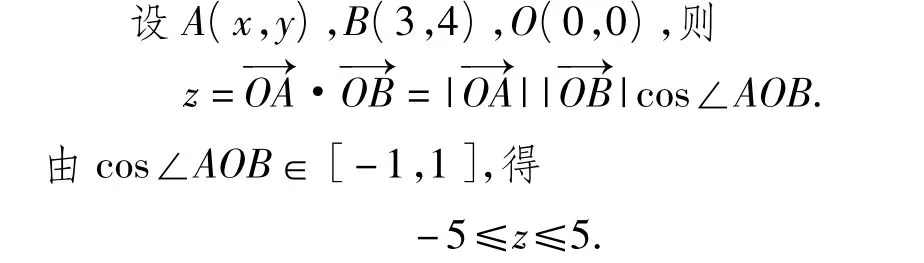
上述幾種解法復習了線性規劃求最值、判別式法求最值、圓的參數方程、向量的數量積等高中數學的主干知識，同時也涉及到函數方程、數形結合、轉化化歸等重要的數學思想方法，正可謂“以小見大，一舉多得”.因此，在教學預設中，若能選擇適當的例題，并引導學生進行多角度的思考與探索，則可實現知識與技能、思想與方法等各方面數學基本功的復習與鞏固、融合與交匯.

2 一法多題，培養學生的收斂性思維

“一法多題”要求學生學會將含某一知識點的習題進行分類整合，歸納出其共同的解題方法和技巧，從而培養學生的收斂性思維和綜合歸納能力.它通過對知識的梳理、歸納、提煉，并在異中求同，從而揭開不同問題的表面現象，挖掘出知識的本質結構，掌握知識的規律性，從而使學生脫離題海，獲得事半功倍的效果.

案例2 設拋物線y2=4x，過點P(2，0)的直線 l交拋物線于點A(x1，y1)，B(x2，y2)，求 AB 中點Q的軌跡.

該例題是筆者在復習“直線與圓錐曲線位置關系”時采用的一個例子，問題牽涉到直線與圓錐曲線相交弦的中點問題，可以采用設而不解的方法，用韋達定理進行求解.在平時的練習中，經常會遇到此類問題，為徹底解決此類問題，筆者布置給學生一個課外作業，要求學生對該例題進行適當的變式，總結歸納并編擬出幾種常見例題.實踐證明，學生的創造能力遠遠超出教師的想象，筆者摘錄了部分學生編擬的典型例題.

例1 設拋物線y2=4x，過點P(2，0)的直線l交拋物線于點 A(x1，y1)，B(x2，y2)，求△AOB 重心G的軌跡.

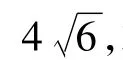
例3 設拋物線y2=4x，過點P(2，0)的直線l交拋物線于點 A(x1，y1)，B(x2，y2).若 S△AOB=8，求此時直線AB的方程.

例4 設拋物線y2=4x，過點P(2，0)的直線l交拋物線于點 A(x1，y1)，B(x2，y2)，證明△AOB 是鈍角三角形.

案例2以及例題1～5都是直線與圓錐曲線相交弦的問題，牽涉到中點、三角形重心、弦長、三角形面積、向量內積、向量共線等問題.這些問題都可以采用設而不解的方法，用韋達定理進行求解，其解題程序基本一致，因此可以對它們進行歸納總結，實現適度的形式化.筆者建議，在解完一道典型例題后，教師要引導學生通過聯想、拓展和深究，舉一反三，并適時地將解題經驗實現發散性和收斂性遷移，以進一步擴大“戰果”，從而獲得較熟練的解題技能.因此，通過引導學生進行例題的歸納總結，可實現“一法多題”教學，從而提高課堂的教學效率和學生的學習效率.

3 一題多得，培養學生的創造性思維

“一題多得”要求學生能對問題進行類比遷移、歸納推廣，能提出個人的猜想，并證明或否定，從而得到新的問題、新的結論.它通過一個問題的教學過程，形成“問題蘑菇群”，從而喚起學生的問題意識.問題意識是創新的基石，是培養創新精神的起點，也是培養創新人才的有效方法.因此在教學中，應用“一題多得”的教學方法，能有效鍛煉學生的類比思維、求異思維和創造性思維能力.

(1)求橢圓C的方程.

(2)E，F是橢圓C上的2個動點.如果直線AE的斜率與AF的斜率互為相反數，證明直線EF的斜率為定值，并求出這個定值.

(2009年遼寧省數學高考理科試題)

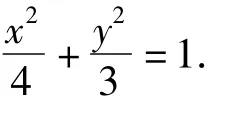
(證明略.)

該題是筆者在授課中所采用的一個例題，講解完畢后，筆者發現：點A的橫坐標恰與橢圓右焦點的橫坐標相同，直線EF的斜率恰為橢圓的離心率e.那么是否所有的橢圓都有上述性質呢?筆者建議對此問題進行推廣探究，得到以下命題.

考慮將橢圓一般化，有：

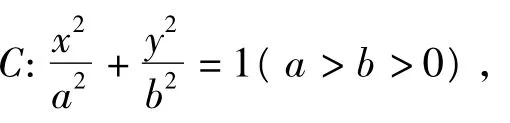
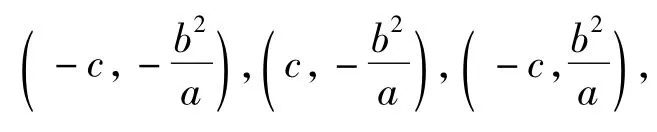
橢圓具有上述性質，在圓錐曲線內進行平行類比，在雙曲線中是不是也有相同的性質?于是筆者引導學生繼續探究，得：

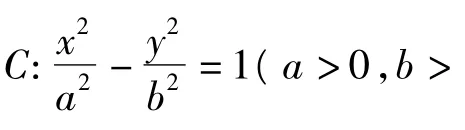
橢圓和雙曲線都稱之為有心圓錐曲線，它們具有極為相似的性質.但是，它們所共有的性質不一定能類比推廣到拋物線，那么在拋物線中是不是也有上述性質呢?回答是肯定的.

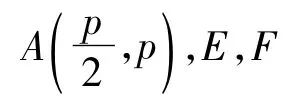
從命題1～3可歸納出圓錐曲線所共有的一個優美性質：

命題4 已知A是圓錐曲線C上一個定點，E，F是圓錐曲線C上的2個動點.若點A與曲線一個焦點的連線垂直于對稱軸，且 kAE+kAF=0，則|kEF|=e.

完成了從橢圓到雙曲線、拋物線的類比，本應結束探究，但為了使學生對圓錐曲線問題有更進一步的理解，筆者引導學生課后進行再探究：當點A為曲線上任意一定點，是否還能得到如此優美的性質?繼續探究可得：

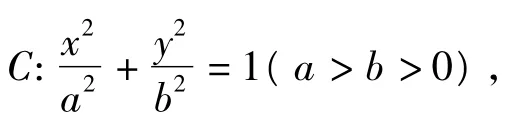
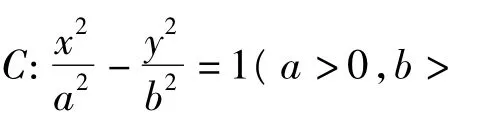
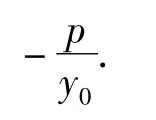
探究沒有停止，接著引導學生嘗試把點A移到曲線外，得到：

命題8 已知M，N，P，Q為圓錐曲線C上不同的4個點.若 kMN+kPQ=0，則 kMQ+kPN=0，kMP+kNQ=0.

教育家波利亞曾說：“學習任何知識的主要途徑即是由自己去發現，因為這一發現，理解最深刻、也最容易掌握其中的內在規律、性質和聯系.”隨著課程教學改革的深入開展，在實施素質教育的今天，要培養學生的創新意識和實踐能力，其中一條很重要的途徑就是讓學生在數學學習中經歷知識的探索過程.也只有在這個過程中，學生才會有體驗、有發展，也就是說要變原來的“聽數學”、“學數學”為“做數學”，讓學生在做中學，在做中獲得不斷發展.

［1］ 楊蒼洲，陳一平.設而不解 事半功倍［J］.數學教學通訊，2009(35)：34-35.