一題三解,各具特色

430223 武漢市光谷實驗中學 沈占立

一題三解,各具特色

430223 武漢市光谷實驗中學 沈占立

近幾年來,武漢市中考題第12題是一道選擇題的壓軸題,亦是一道多結論判斷型問題,題目涉及的知識點多,綜合性強,解法靈活多樣.茲以武漢市2011年第12題為例予以說明.

如圖1,在菱形ABCD中,AB=BD,點E,F分別在AB,AD上,且AE=DF.連接BF與DE相交于點G,連接CG與BD相交于點H.有下列結論：

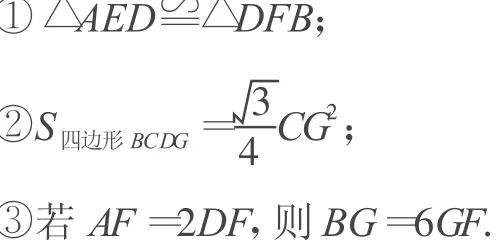
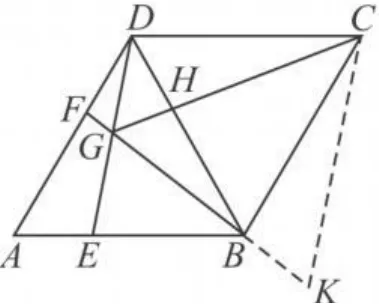
圖1

其中正確的結論有

本題結論①顯然成立,結論③也不難得證.很多考生卻在結論②上失分較多.本文就此列舉三種解法,供讀者參考.

1 常規解法——構造全等

證明 延長 GB至K,使BK=DG,連接CK.如圖1.∵四邊形ABCD是菱形,AB=BD,∴△ABD和△BCD都是等邊三角形,∴AD=BD,∠DAE=∠BDF=60°,又∵AE=DF,∴△AED≌△DFB,∴∠ADE=∠DBF,∴∠BGE=∠DBF+∠BDG=∠ADE+∠BDG=∠ADB=60°,∴∠BGD=120°,又∠BCD=60°,∴∠CBG+∠CDG=180°,又∠CBG+∠CBK=180°,∴∠CDG=∠CBK,∴△CDG≌△CBK.∴CG=CK,∠DCG=∠BCK,∴∠GCK=∠DCB=60°,

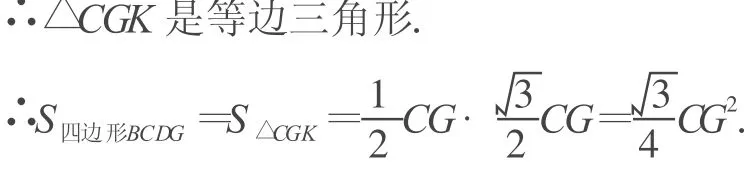
點評 上述解法不失一般性,雖然解法較繁,但易于理解.

2 標新立異——旋轉變換

證明 如圖 2所示,將△CDG以點C為旋轉中心逆時針旋轉60°,得到△CBM,

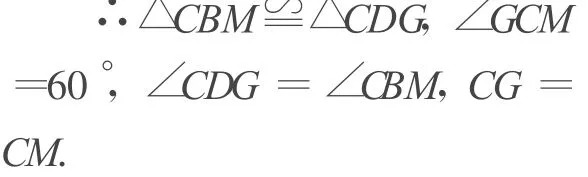
圖2

點評 本種解法較簡單,也較特殊,頗具創意.

3 巧思妙解——足夠地退

證明 當E為AB的中點時,F亦為AD的中點,如圖3,

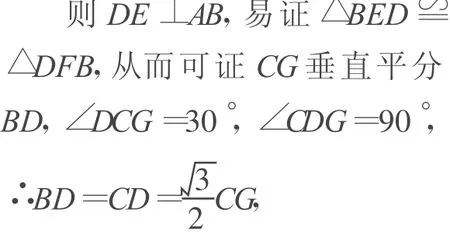
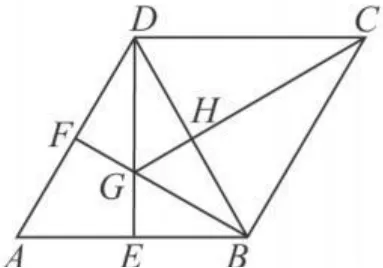
圖3

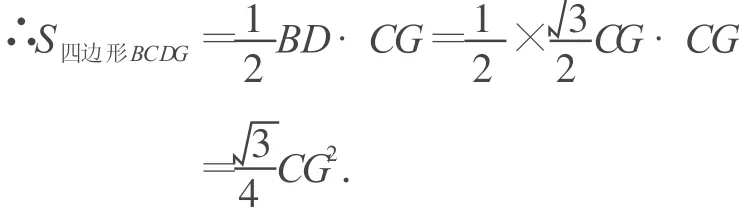
點評 本解法最簡單,也最特殊(取E點為特殊點又不失題意),思維發散達到極點.

數學大師華羅庚曾經說過：“善于‘退’,足夠地‘退’,退到最原始又不失重要性的地方去研究,是學好數學的一個訣竅！

20110807)