基于減量學習的魯棒稀疏最小二乘支持向量回歸機

高潤鵬，傘 冶，朱 奕

（哈爾濱工業大學控制與仿真中心，黑龍江 哈爾濱 150001）

0 引言

支持向量機［1］（support vector machine，SVM）是Vapnik提出的一種基于統計學習理論的學習機器，與神經網絡相比，它可以解決小樣本、“維數災”和局部極值解等問題，具有較強的泛化能力，并在目標聲識別［2］、爆破震動預測［3］等實際問題中得到廣泛應用。它采用自上而下的學習方式，選取損失函數如ε不敏感損失函數、Laplacian損失函數、Huber損失函數或分段損失函數，得到具有一定魯棒性和稀疏性的模型。

最小二乘支持向量機［4］（least squares SV M，LSSV M）是SV M的擴展算法，求解算法為解線性方程組，訓練速度明顯加快。LSSV M的求解算法主要有共軛梯度法［4］、降階法［5］和序列最小優化算法［6］等。但LSSV M采用誤差的平方和作為損失函數，當數據混有非高斯分布長尾噪聲時，算法魯棒性變差。為此Suykens［7］提出加權LSSV M （weighted LSSV M，WLSSV M），它根據誤差信息賦予樣本權重，對異常樣本賦予極小的權重值以抑制它的影響。但當異常樣本較多時，WLSSV M檢測和抑制異常樣本能力下降。采用迭代 WLSSV M［4］及改進算法［8－9］可增強算法的魯棒性，但需要多次訓練 WLSSV M且訓練時間較長。De Brabanter［10］實驗對比四種權值函數的迭代WLSSV M算法的魯棒性。張淑寧［11］采用魯棒學習提高LSSV M的魯棒性。溫雯［12］采用假設檢驗方法檢測異常樣本，剔除它并使用減量學習更新模型，算法的魯棒性增強。采用以上算法LSSV M魯棒性在一定程度上得到增強，但LSSV M采用等式約束，導致算法缺乏稀疏性，過多的支持向量使得模型結構復雜、預測時間長。因此有學者提出改進算法提高稀疏性，如先學習訓練樣本得到初始模型。1）按剪枝策略選擇部分支持向量，直接刪除它并重新訓練LSSV M，重復該過程直到事先定義的性能指標下降為止。剪枝策略主要有：最小支持向量譜［13］，模型引入誤差最小［14］及其改進算法［15］等。缺點是需要重復訓練LSSV M，計算量較大。2）在高維特征空間采用向量相關分析約簡支持向量［16－17］，約簡模型性能不變，缺點是支持向量約簡率較低。學者提出改進算法［18－20］以提高支持向量約簡率。Yang［21］提出自適應剪枝算法得到模型稀疏解。Zhao［22］將使目標函數值下降較多的樣本加入支持向量集。采用以上算法可提高LSSV M稀疏性，但當數據混有異常樣本時，它卻將異常樣本當作支持向量，算法魯棒性差。為克服前人單一提高魯棒性或稀疏性的缺點，本文提出魯棒稀疏最小二乘支持向量回歸機（least squares support vector regression machine，LSSVRM）算法。它從初始LSSVRM模型出發，自下而上的采用循環逐一刪除異常樣本或不重要樣本。為增強算法魯棒性，采用基于留一誤差的魯棒“3σ”準則檢測并刪除異常樣本。為提高算法稀疏性，采用基于最小絕對留一誤差的剪枝策略刪除不重要樣本。為降低算法計算量，采用快速留一誤差和減量學習更新模型。

1 最小二乘支持向量回歸機

設訓練數據集 ｛ （xi，yi），輸入xi∈Rz，輸出yi∈R，根據結構風險最小化原則，Suykens［4］將損失函數由誤差和轉變為誤差的平方和，約束條件由不等式約束轉變為等式約束，LSSVRM可以表示為如式（1）所示優化問題：

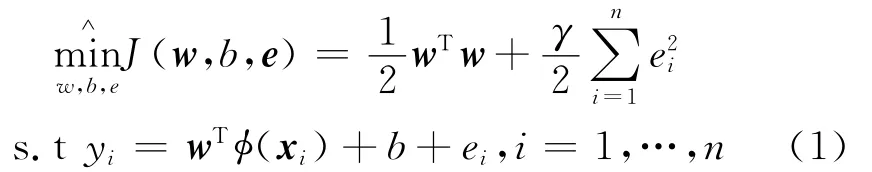
式（1）中，φ（·）是將輸入空間映射到高維特征空間的非線性函數；w表示模型的復雜度；e＝［e1，…，en］T表示經驗誤差；γ∈R＋是正則化參數。為解這個約束優化問題，利用對偶優化和Lagrange函數把約束優化問題轉化為無約束優化問題：

式（2）中，α＝ ［α1，…，αn］T為Lagrange乘子。由最優化條件可得：

式（3）中，y ＝ ［y1，…，yn］T；α ＝ ［α1，…，αn］T；1＝［1，…，1］T；I是 單 位 矩 陣；Κij＝ φ （xi）Tφ（xj）＝k（xi，xj）；k（xi，xj）是核函數，常用的核函數有高斯核函數k（xi，xj）＝exp（－‖xi－xj‖2／ρ2）和多項式核函數k（xi，xj）＝／μ＋1）d。

求解式（3）線性方程組可以得到α和b。回歸函數f（x）如式（4）所示：

2 魯棒稀疏LSSVRM算法

由于設備故障、電磁干擾和過失誤差等因素影響，實際數據不可避免地混入異常值，所以研究LSSVRM的魯棒稀疏算法具有較大的實用價值。因此本文提出魯棒稀疏LSSVRM算法，它采用自下而上的學習方式，首先學習訓練樣本得到初始LSSVRM模型，獲得每個樣本的誤差信息作為先驗知識。采用循環逐一刪除異常樣本方式，即每次循環只考察異常性最大的樣本，判斷它是否是異常樣本，是則刪除該異常樣本，學習剩余樣本更新模型，使回歸曲面能逐步得到糾正，提高下一次循環異常樣本的檢測率，以增強算法魯棒性。當異常樣本刪除完畢，再逐一刪除模型中不重要樣本，并學習剩余樣本更新模型，直到模型泛化性能略有下降為止，以提高算法的稀疏性。

要實現上述算法主要解決以下三個問題：一是采用什么方法檢測異常樣本，二是如何選擇不重要樣本，三是如何快速更新模型，以降低計算量。因此本文采用基于快速留一誤差的魯棒 “3σ”準則檢測異常樣本，選擇具有最小絕對留一誤差的樣本作為不重要樣本，采用減量學習快速更新模型。

2．1 快速留一誤差

留一誤差Δyi是用除第i個樣本外的其余樣本擬合回歸曲面，計算第i個樣本的預測值，則Δyi＝yi－。由于LSSVRM采用誤差的平方和作為損失函數，異常樣本將回歸曲面拉向自身，使異常樣本的誤差減小，正常樣本的誤差增大，而計算樣本的留一誤差過程中回歸曲面沒有該樣本，所以留一誤差較普通誤差更能如實反映樣本的異常性。因此本文采用留一誤差代替普通誤差。但計算訓練樣本的留一誤差相當于訓練n次n－1個樣本的LSSVRM模型，其中n為模型中樣本個數。計算復雜度為O（n4），計算量非常大，不適合訓練樣本較多的情況。但采用快速留一誤差［23］，在得到LSSVRM模型的基礎上，只進行簡單運算即可得到所有訓練樣本的留一誤差，計算復雜度降為O（n），降低了計算量。第i個樣本的留一誤差Δyi如式（5）所示。

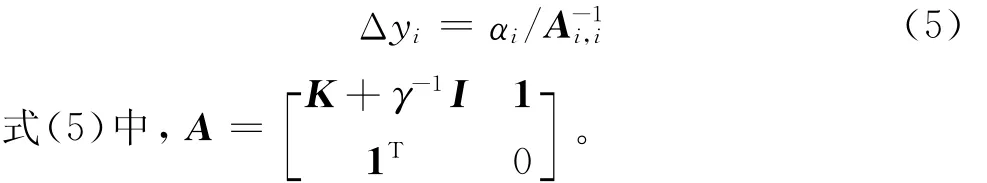
下面以計算第一個樣本的留一誤差為例，簡要推導快速留一誤差的計算公式，由式（3）可知，

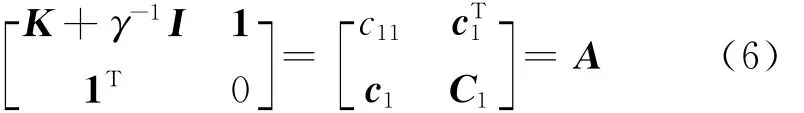
式（6）中，c1＝ ［k（x2，x1），…，k（xn，x1），1］T；c11＝k（x1，x1）＋γ－1；C1由矩陣A去掉第一行和第一列得到。

刪除第一個樣本（x1，y1），學習剩余樣本得到模型參數α（－1），b（－1），如式（7）所示。

由式（3）和式（6）可得從第2到n＋1個等式方程。

由式（3）線性方程的第一個等式方程得：

結合式（10）和式（11）得：

由方塊矩陣求逆引理可得：

因為樣本順序可以任意調換，所以推廣到所有訓練樣本，第i個樣本的留一誤差Δyi為：

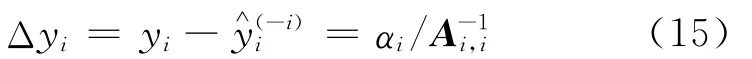
由于A－1已知，由式（15）可知，通過簡單計算即可快速得到所有訓練樣本的留一誤差。

2．2 基于留一誤差的魯棒“3σ”準則檢測異常樣本

由于訓練數據含有異常樣本，樣本的留一誤差分布具有長尾性，不符合N（0，σ2）標準高斯分布，基于均值和方差的普通“3σ”準則對異常誤差敏感，魯棒性差，所以采用它檢測異常樣本的能力急劇下降。因此本文采用魯棒“3σ”準則［24］，按式（16）計算第i個樣本的標準留一誤差：

因此，異常樣本的判斷準則為樣本的標準留一誤差SLOOi是否大于閾值c，大于c則為異常樣本，否則為正常樣本。

異常樣本檢測停止條件：樣本最大標準留一誤差不大于閾值c，即max（SLOOi）≤c。c值越大，檢測到異常樣本的數目相對越少，將異常樣本當作正常樣本的機率越大。反之，c值越小，檢測到異常樣本的數目相對越多，將正常樣本當作異常樣本的機率越大。對于異常樣本不太多的情況，取c＝3較合適，因為對于符合標準高斯分布誤差，SLOOi＞3的概率是0．26%。對于異常樣本較多的情況，取c＝2．5較合適。

2．3 基于最小絕對留一誤差的剪枝策略

由于LSSVRM模型缺乏稀疏性，為得到稀疏模型，采用剪枝策略刪除不重要樣本使得模型結構簡單、預測時間短，但同時模型會損失部分信息，從而導致模型泛化性能下降。樣本剪枝策略主要有Suykens［13］提出的刪除較小的樣本，因為ei＝αi／γ，相當于構造誤差不敏感域，但刪除該樣本后模型引入誤差不保證最小，因此按此剪枝策略得到的稀疏模型泛化性能不理想。De Kr uif［14］提出刪除模型引入誤差最小的樣本，如式（18）所示。但當γ＝∞時，相當于目標函數沒有正則化項，矩陣B經常奇異，而且計算矩陣B的逆矩陣計算量較大；當γ＜∞時，需要進行復雜矩陣運算。

式（18）中，di＝［0，…，0，1，0，…，0］T，di中第i個元素為1K是核矩陣；Y ＝ ［y1，…，yn，0］T。Kuh［15］提出刪除具有最小的樣本，它是刪除樣本后模型引入誤差的另一種計算公式。本文采用刪除具有最小絕對留一誤差的樣本，因為由可知，刪除arg min（）樣本對模型的引入誤差最小，所以模型信息損失相對較小，模型泛化性能也相對要好。

剪枝停止條件是樣本最小絕對留一誤差大于閾值ζ，即min（）＞ζ。閾值ζ決定被刪除不重要樣本的個數，ζ值越大，則被刪除不重要樣本個數越多，模型泛化性能越差。反之，ζ值越小，則被刪除不重要樣本個數越少，模型泛化性能相對越好。閾值ζ的取值與具體數據集樣本的輸出有關，要在模型稀疏性和泛化性能取折衷，由實際應用需求決定。

2．4 減量學習

假設當前LSSVRM模型由N個樣本建立，刪除一個樣本后，需要訓練剩余N－1個樣本以得到新模型，訓練算法計算復雜度為O（（N－1）3），計算量較大。為減少計算量，降低計算復雜度，采用減量學習更新模型，計算復雜度降為O（（N－1）2）。

設當前模型由N個樣本建立，即ANaN＝YN，且

從模型中刪除樣本 （xk，yk），則新模型參數為

為避免矩陣AN－1求逆，A由式（20）得到［25］

則N－1個樣本對應的LSSVRM模型參數aN－1＝ ［αb］T，可由式（19）得到。

2．5 算法復雜度分析

設當前LSSVRM模型由N個樣本建立，不論是采用2．2節基于留一誤差魯棒“3σ”準則檢測異常樣本或2．3節基于絕對最小留一誤差的剪枝策略，均采用2．1節快速留一誤差公式（5）計算所有樣本的留一誤差，計算復雜度為Ο（N）。然后通過減量學習刪除一個樣本后得到由（N－1）個樣本建立的模型，則執行一次減量學習的計算復雜度為Ο（（N－1）2）。魯棒稀疏LSSVRM算法刪除所有異常樣本和不重要樣本的總計算復雜度為：

式（21）中，Noutlier是異常樣本的個數，m是被刪除不重要樣本的個數。但異常樣本和被刪除不重要樣本的總數小于訓練樣本，總計算復雜度小于直接訓練一次LSSVRM復雜度Ο（n3）。加上2．2節異常樣本檢測階段計算標準留一誤差過程中的中位數等計算，則魯棒稀疏LSSVRM算法總計算量與加權LSSVRM相當，即相當于訓練兩次LSSVRM，所以算法訓練時間和加權LSSVRM訓練時間接近。

2．6 完整算法流程

魯棒稀疏LSSVRM算法步驟如下：

Step1：學習訓練樣本得到初始LSSVRM模型。

Step2：按式（5）和式（16）計算訓練樣本標準留一誤差，判斷樣本最大標準留一誤差是否大于閾值c，是則刪除該異常樣本，并采用減量學習更新模型，返回Step2；否則異常樣本檢測和刪除階段停止，轉向Step3。

Step3：按式（5）計算訓練樣本的留一誤差，判斷樣本最小絕對留一誤差是否小于或等于閾值ζ，是則刪除該樣本，并采用減量學習更新模型，返回Step3；否則輸出魯棒稀疏LSSVRM模型。

魯棒稀疏LSSVRM算法流程圖如圖1所示。

圖1 魯棒稀疏LSSVRM算法流程圖Fig．1 The flowchart of r obust sparse LSSVRM algorith m

3 數值仿真

本文實驗在2．7 GHz奔騰雙核處理器，2 GB內存的臺式機進行，程序由Matlab7．10實現。選用高斯核函數，LSSVRM模型參數為正則化參數γ和高斯核參數ρ2，最優參數由留一交叉驗證法［23］確定。噪聲環境下回歸模型的性能評價指標：

1）測試絕對平均誤差，如式（22）所示：

式（22）中，Ntest是測試樣本的個數。

2）統計學家［25］提出如式（23）所示指標：

合理模型R2的取值范圍是0≤R2≤1。R2＝1表示最佳擬合，當R2＜0時，說明模型已到達“崩潰點”。

算法說明：本文算法魯棒稀疏LSSVRM（r obust sparse LSSVRM，RSLSSVRM），對比算法有LSSVRM、加權LSSVRM （weighted LSSVRM、WLSSVRM），魯棒 LSSVRM （r obust LSSVRM，RLSSVRM），它是本文算法只進行異常樣本檢測和刪除階段得到的魯棒LSSVRM模型，用于考察本文算法的魯棒性。

3．1 仿真數據集

仿真數據集中訓練樣本由采樣函數sinc（x）和噪聲函數Fε（e）疊加產生，sinc（x）在［－10，10］內等間隔采樣產生，個數為200。采用式（24）生成噪聲：

式（24）中，F0（e）是符合 N（0，0．09）的高斯噪聲；H（e）是異常噪聲；ε是異常樣本占訓練樣本的比例，0≤ε≤1。H（e）為產生異常樣本的噪聲，本文采用符合［－1，3］均勻分布噪聲。為全面考察算法的性能，異常樣本占訓練樣本的比例ε從5%開始以5%的增幅增加至45%，異常樣本在定義域內隨機產生，生成9個訓練集。測試樣本由采樣函數sinc（x）在［－10，10］等間隔采樣產生，不含噪聲，個數為200。參數設置為：γ＝10，ρ2＝1，閾值c＝3，閾值ζ＝0．05。四種算法在9個訓練集上的實驗結果如表1所示，對比指標有：MAE、R2和訓練時間（training ti me，TT）。

首先考察算法的魯棒性，各算法初次到達“崩潰點”時R2數據已加下劃線，由表1可以看出，當異常樣本占訓練樣本比例較低時，如ε為5%、10% 時，RLSSVRM和WLSSVRM的魯棒性能都很好，但RLSSVRM的性能優于 WLSSVRM。當ε增加至15%和20%時，WLSSVRM性能下降，但還沒有到達“崩潰點”，而RLSSVRM魯棒性能依然很強。對于LSSVRM，當ε＝10%時，R2已為負數，說明模型預測結果不合理，由此可見LSSVRM對異常樣本非常敏感。當異常樣本比例為25% 時，WLSSVRM的R2＝－0．781 5，算法已到達“崩潰點”，此時 MAE＝0．156 7，預測結果已不合理。而RLSSVRM魯棒性一直很好，直到異常樣本比例達到45% 時，R2＝－0．065 5，已到達算法的“崩潰點”，MAE ＝0．121 2。這是因為異常樣本比例已接近50%，初始LSSVRM模型幾乎無法提供有價值信息，正常樣本和異常樣本的留一誤差相差不大，所以基于中位數和魯棒標準差的“3σ”準則也很難辨別正常樣本和異常樣本。

從算法訓練時間看，9個訓練集上，RSLSSVRM和WLSSVRM訓練時間接近，實驗結果與2．4節算法復雜度分析結果吻合。

再考察算法的稀疏性，由表1實驗結果可以看出，異常樣本比例ε是5%、20%、30%、35%和40%時，RSLSSVRM在得到RLSSVRM基礎上，通過不斷刪除絕對留一誤差最小的樣本使模型稀疏，因此損失部分模型信息，所以RSLSSVRM模型的MAE和R2比RLSSVRM模型性能略差。而異常樣本比例ε是10%、15%和25%時，RSLSSVRM模型的MAE和R2優于RLSSVRM模型，這是因為稀疏模型結構簡單，泛化性能可能更好，有時對誤差較小樣本的過分擬合，可降低模型的泛化性能。

為分析閾值c對RSLSSVRM算法魯棒性的影響，固定閾值ζ＝0．05，c值分別取2．5、3和3．5，在9個訓練集進行實驗，對比指標為：異常樣本個數（nu mber of outliers，NO）、MAE和R2，實驗結果如表2所示。由表2可以看出，RSLSSVRM算法在c＝［2．5，3．5］取得了較好的魯棒性。隨著c值的減小，檢測的異常樣本數目增多，如c＝2．5時，當異常樣本數目較少時，由于很多正常樣本被當作異常樣本被刪除，導致模型MAE和R2相對較差。隨著c值的增大，檢測的異常樣本數目減少，如c＝3．5時，當異常樣本較多時，由于很多異常樣本被當作正常樣本而被保留，也導致模型MAE和R2相對較差。所以對于異常樣本不太多時取c＝3較合適；異常樣本較多時，取c＝2．5；實驗結果也驗證了2．2節理論分析。

為分析閾值ζ對RSLSSVRM算法稀疏性的影響，固定閾值c＝3，ζ值分別取0．02、0．05和0．08，在9個訓練集進行實驗，對比指標：被刪除不重要樣本個數（number of eli minated uni mportant samples，NEUS）、MAE和R2，實驗結果如表3所示。由表3可以看出，隨著ζ值增大，被刪除的不重要樣本明顯增多，RSLSSVRM模型信息損失越多，模型MAE和R2性能越差。隨著ζ值減小，被刪除的不重要樣本越少，RSLSSVRM模型信息損失越少，模型的MAE和R2性能相對要好。考慮到模型的稀疏性和泛化性能的折衷，實際應用中根據需求確定閾值ζ，對于仿真數據集取ζ＝0．05較合適，實驗結果也驗證了2．3節理論分析。

表1 4種算法在仿真數據集上的測試結果Tab．1 Testing results of four algorith ms on si mulation datasets

表2 閾值c對RSLSSVRM算法魯棒性的影響Tab．2 Threshold c effects on the robustness of RSLSSVRM algorith m

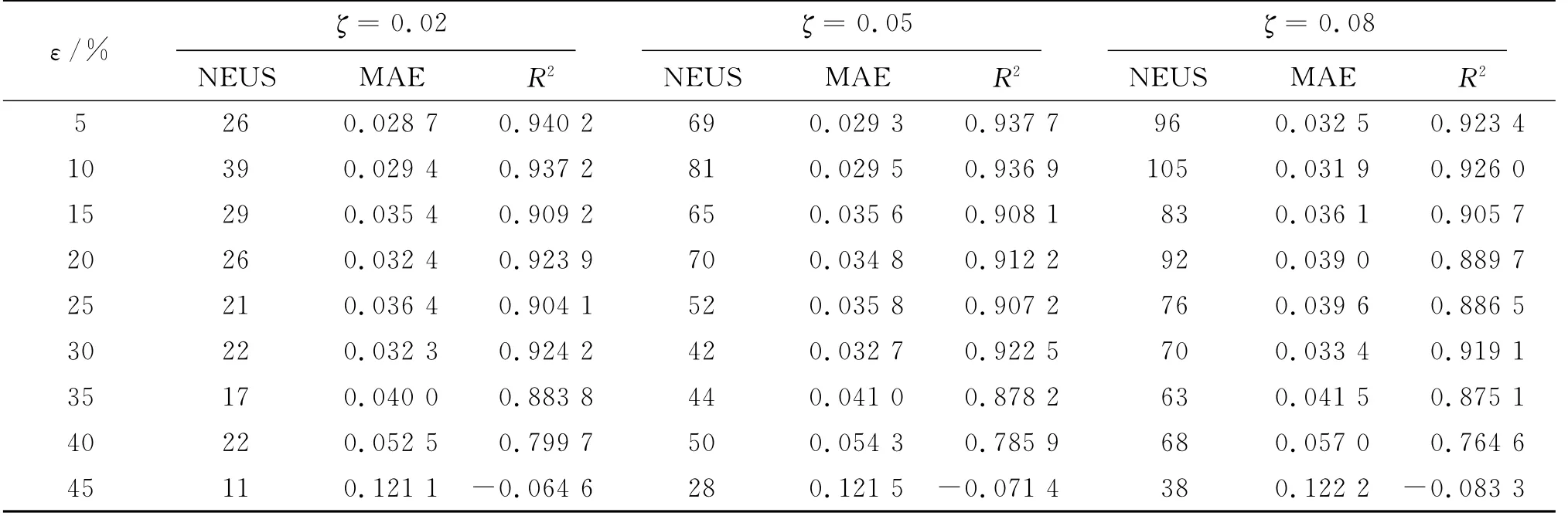
表3 閾值ζ對RSLSSVRM算法稀疏性的影響Tab．3 Thresholdζeffects on the sparseness of RSLSSVRM algorith m

3．2 標準數據集

為進一步測試算法的有效性，采用5個標準數據集［26］：Triazines、Bodyfat、Mpg、Housing和 Mg，輸入數據歸一化為［0 1］，輸出數據不變，數據集描述和參數設置如表4所示。4種算法在5個標準數據集上實驗結果如表5所示。對比指標有：異常樣本個數NO、被刪除不重要樣本個數NEUS、R2和訓練時間TT。由表5可以看出，與WLSSVRM相比，在魯棒性方面RLSSVRM均取得較好的擬合性能。在稀疏性方面，在數據集Bodyfat、Mpg和Mg，RSLSSVRM在大幅減少支持向量的同時，擬合性能略差于RLSSVRM，但在數據集Triazines和Housing，RSLSSVRM擬合性能優于RLSSVRM。總體上，標準數據集實驗結果表明RSLSSVRM性能優于WLSSVRM和LSSVRM。在訓練時間方面，RSLSSVRM所需時間與WLSSVRM相當。

表4 數據集描述與參數設置Tab．4 Dataset descriptions and parameter setting

4 結論

為解決LSSVRM在噪聲環境下魯棒性不強和缺乏稀疏性問題，在得到初始LSSVRM模型基礎上，提出采用自下而上的學習方式和基于減量學習逐一刪除異常樣本或不重要樣本的魯棒稀疏LSSVRM算法。并采用基于快速留一誤差的魯棒“3σ”準則檢測異常樣本和基于最小絕對留一誤差的剪枝策略刪除不重要樣本。理論分析和數據集實驗結果表明：采用基于留一誤差的魯棒“3σ”準則檢測并刪除異常樣本后，新算法魯棒性明顯增強；采用基于最小絕對留一誤差的剪枝策略刪除不重要樣本后，在模型泛化性能略有下降的情況下，支持向量數目大幅減少，新算法稀疏性明顯提高；采用快速留一誤差和減量學習更新模型后，降低了計算量，新算法訓練時間與WLSSVRM訓練時間相當。

［1］Vapnik V N．The nature of statistical lear ning theory［M］．New Yor k：Springer－Verlag，1995．

［2］李京華，張聰穎，倪寧．基于參數優化的支持向量機戰場多目標聲識別［J］．探測與控制學報，2010，32（1）：1－5．LI Jinghua，ZHANG Chongying，NI Ning．Multi－target acoustic identification in battlefield based on SV M of parameter opti mization［J］．Jour nal of Detection ＆Control，2010，32（1）：1－5．

［3］丁凱，方向，陸凡東，等．基于支持向量機的振動加速度峰值預測模型［J］．探測與控制學報，2010，32（4）：38－41．DING Kai，FANG Xiang，LU Fandong，et al．Forecasting model of blasting vibration acceleration peak－value based on SV M［J］．Jour nal of Detection ＆ Contr ol，2010，32（4）：38－41．

［4］Suykens J A K，Van Gestel T，De Brabanter J，et al．Least squares support vector machines［M］．Singapore：World Scientific，2002．

［5］Chu W，Ong C J，Keerthi S S．An i mproved conjugate gradient scheme to t he solution of least squares SV M［J］．IEEE Trans on Neural Net works，2005，16（2）：498－501．

［6］Keerthi S S，Shevade S K．SMO algorith m for leastsquares SV M for mulations［J］．Neural Co mputation，2003，15（2）：487－507．

［7］Suykens J A K，De Brabanter J，Lukas L，et al．Weighted least squares support vector machines：robustness and sparse approxi mation［J］．Neurocomputing，2002，48：85－105．

［8］呂劍峰，戴連奎．加權最小二乘支持向量機改進算法及其在光譜定量分析中的應用［J］．分析化學，2007，35（3）：340－344．LU Jianfeng，DAI Liankui．Improved weighted least squares support vector machines algorith m and its applications in spectroscopic quantitative analysis［J］．Chinese Jour nal of Analytical Chemistr y，2007，35（3）：340－344．

［9］包鑫，戴連奎．加權最小二乘支持向量機穩健化迭代算法及其在光譜分析中的應用［J］．化學學報，2009，67（10）：1 081－1 086．BAO Xin，DAI Liankui．Robust iterative algorit h m of weighted least squares support vector machine and its application in spectral analysis［J］．Acta Chi mica Sinica，2009，67（10）：1 081－1 086．

［10］De Brabanter K，Pelck mans K，De Brabanter J，et al．Robustness of ker nel based regression：a co mparison of iterative weighting schemes［C］／／Berlin，Ger many：Springer－Verlag，2009．

［11］張淑寧，王福利，尤富強，等．基于魯棒學習的最小二乘支持向量機及其應用［J］．控制與決策，2010，25（8）：1 169－1 172．ZHANG Shuning，WANG Fuli，YOU Fuqiang，et al．Robust least squares support vector machine based on robust learning algorith m and its application［J］．Control and Decision，2010，25（8）：1 169－1 172．

［12］溫雯，郝志峰，楊曉偉，等．基于假設檢驗及異常點剔除的穩健LS－SV M 回歸［J］．模式識別與人工智能，2010，23（2）：241－249．WEN Wen，HAO Zhifeng，YANG Xiaowei，et al．Robust least squares support vector machine regression based on hypothesis testing and outlier－eli mination［J］．Patter n Recognition and Artificial Intelligence，2010，23（2）：241－249．

［13］Suykens J A K，Lukas L，Vandewalle J．Sparse approximation using least squares support vector machines［C］／／Geneva，Switzerland：IEEE Press，Florida，2000．

［14］De Kr uif B J，De Vries T J A．Pr uning err or mini mization in least squares support vector machines［J］．IEEE Trans on Neural Net wor ks，2003，14（3）：696－702．

［15］Kuh A，De Wilde P．Comments on"Pruning error minimization in least squares support vector machines"［J］．IEEE Trans on Neural Net wor ks，2007，18（2）：606－609．

［16］甘良志，孫宗海，孫優賢．稀疏最小二乘支持向量機［J］．浙江大學學報（工學版），2007，41（2）：245－248．GAN Liangzhi，SUN Zonghai，SUN Youxian．Sparse least squares support vector machine［J］．Jour nal of Zhejiang University （Engineering Science），2007，41（2）：245－248．

［17］Liang X，Chen R C，Guo X Y．Pruning support vector machines without altering perfor mances［J］．IEEE Trans on Neural Net works，2008，19（10）：1 792－1 803．

［18］陳愛軍，宋執環，李平．基于矢量基學習的最小二乘支持向量機建模［J］．控制理論與應用，2007，24（1）：1－5．CHEN Aijun，SONG Zhihuan，LI Ping．Modeling method of least squares support vector regression based on vector base learning［J］．Control Theory ＆ Applications，2007，24（1）：1－5．

［19］Liang X．An effective method of pr uning support vector machine classifiers［J］．IEEE Trans on Neural Net works，2010，21（1）：26－38．

［20］Li Q，Jiao L C，Hao Y J．Adaptive si mplification of solution for support vector machine［J］．Patter n Recognition，2007，40（3）：972－980．

［21］Yang X W，Lu J，Zhang G Q．Adaptive pr uning algorit h m f or least squares support vector machine classifier［J］．Soft Co mputing，2010，14（7）：667－680．

［22］Zhao Y P，Sun J G．Recursive reduced least squares support vector regression［J］．Patter n Recognition，2009，42（5）：837－842．

［23］Cawley G C，Talbot N L C．Preventing over－fitting during model selection via bayesian regularisation of the hyper－parameters［J］．Jour nal of Machine Lear ning Research，2007，8（4）：841－861．

［24］Maronna R A，Martin R D，Yohai V J．Robust statistics：t heor y and methods［M］．England：John Wiley ＆Sons，2006．

［25］Cau wenberghs G，Poggio T．Incremental and decremental support vector machine learning［C］／／Cambridge，MA：MIT Press，2001．

［26］Chang C C，Lin C J．LIBSV M：a library f or support vector machines［EB／OL］．［2011－06－15］htt p：／／www．csie．ntu．edu．t w／～cjlin／libsv mtools／datasets／regression．