基于貝葉斯估計的加權最小二乘分布式融合

徐 蘇，楊 紅

（1.淮海工學院工程訓練中心，江蘇 連云港 222000；2.廣州大學物理與電子工程學院，廣東 廣州 510006）

0 引言

多傳感器信息融合技術廣泛應用于軍事、國防、目標跟蹤、GPS定位、機器人、信號處理、通信、控制等領域，目前成為備受人們關注的熱門領域。信息融合的目的就是將多傳感器信息進行有效地處理，從而得到比單一傳感器更加精確的結果。對于基于Kal man濾波的多傳感器觀測數據融合，主要有狀態融合和測量融合。測量融合可分為集中式融合和分布式融合［1］。

文獻［2］提出了不同觀測矩陣的最小二乘數據融合算法，文獻［3］提出了按對角陣加權的最小二乘數據信息融合算法，文獻［4］對按矩陣、對角陣、標量3種加權方法進行了比較，文獻［5］將算法擴展，提出了不同觀測矩陣加權最小二乘算法，但這些方法的一個共同缺點是沒有考慮到模型參數本身的信息，因此深入研究基于貝葉斯估計的帶不同觀測矩陣的加權最小二乘分布式融合Kal man濾波算法，可以提高融合算法的性能，非常有實際意義。

1 卡爾曼濾波和貝葉斯估計

1.1 非線性卡爾曼濾波系統

1960年，卡爾曼發表了用遞歸方法解決離散數據線性濾波問題的論文。得出系統的狀態隨機差分方程，用如下狀態空間模型描述的動態系統：

式中，t表示離散時間，系統在時刻t的狀態X（t）∈Rn，W（t）∈Rr為輸入白噪聲，Y（t）∈Rm是對狀態的觀測信號，v（t）∈Rm為觀測噪聲。F、G和H 分別為n×n、n×r和m×n的己知矩陣，分別稱F為狀態轉移矩陣，G為過程噪聲分布矩陣，H為觀測矩陣稱式（1）為狀態方程，稱式（2）為觀測方程。

如果存在多個觀測方程，就涉及到如何利用多個觀測數據得到最優的狀態X（t）的問題。這涉及到數據融合問題，最小二乘估計是一種常見的融合方法［6］。

而對于非線性系統的卡爾曼濾波問題，一般需要在線性濾波理論的基礎上，通過線性化處理，構成解非線性濾波問題的次優濾波算法來處理這類問題。目前廣泛使用的是推廣的離散卡爾曼濾波，這種方法不同于線性化離散Kal man濾波，即不需預先算出狀態矢量的理想軌跡，而預先算出狀態矢量的理想軌跡在實際工作中可能會遇到困難［7］。

1.2 最小二乘估計

考慮線性模型

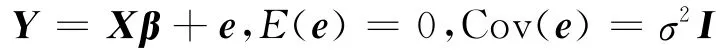
的參數β和σ2的估計問題，最小二乘估計的思想是β的真值是使e＝Y－Xβ達到最小，也就是其長度平方

達到最小，則得到β的估計為

1.3 貝葉斯估計

貝葉斯理論提供了一種計算假設概率的方法，基于假設的先驗概率、給定假設下觀察到不同數據的概率以及觀察到的數據本身，來計算后驗概率一般地，設θ為未知參數（可以為向量），它的驗前密度記為π（θ），Y為觀測量，于是在獲得觀測之后，θ的驗后密度由Bayes公式給出［8］。

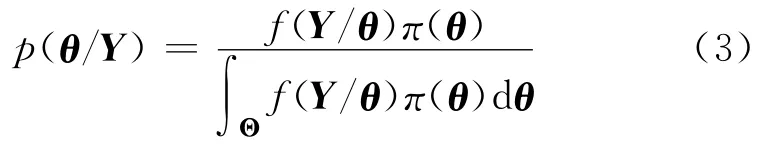
式（3）中，f（Y／θ）為θ給定時Y 的概率密度函數，Θ為θ的參數空間。在進行Kal man濾波融合時，考慮模型參數本身的先驗信息條件，應用貝葉斯估計可以提高融合精度。

2 基于貝葉斯估計的非線性離散系統的加權最小二乘分布式融合

實際上，絕大多數情況下Kal man濾波系統都是非線性系統，因此考慮非線性系統的數據融合問題，具有很強的現實意義。由于非線性系統的復雜性，本文先采用推廣的離散卡爾曼濾波對非線性系統線性化，在線性化基礎上，提出基于Bayes估計的加權最小二乘分布式融合。

2.1 非線性離散系統的線性化

實際應用中，許多系統并非完全線性，因此不同觀測陣的隨機非線性離散多傳感器系統模型可描述為：

式（4）中，t為離散時間，X（t）∈Rn為狀態，Yi（t＋1）∈Rmi為第i傳感器在t＋1時刻的觀測值，vi（t＋1）∈Rmi為第i傳感器在t＋1時刻的觀測噪聲，W（t）∈Rr為輸入白噪聲，f（·），g（·）和hi（·）對X（t）是可微的。對于式（4），可以采用推廣的離散卡爾曼濾波進行線性化處理。

假設1：W（t）∈Rr和vi（t）∈Rmi（i＝1，…，L）為零均值不相關高斯白噪聲，且vi（t）和X（t）不相關，而vi（t）和vj（t）（i≠j）是相關觀測高斯白噪聲，則

式（5）中，E為均值號，T為轉置號，δtt＝1，δth＝0（t≠h），Q＞0。如果在t時刻，狀態矢量X（t）的線性最小均方誤差估計X^（t）已知，那么就可以把系統信號模型式（4）在X（t）＝X^（t）附近展開成泰勒級數，取其一次項，其中，離散狀態一步預測為：

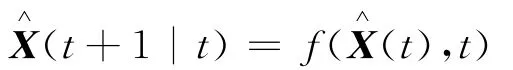
并認為g（X（t），t）＝g（X^（t），t），這樣離散系統的信號模型可以寫成和

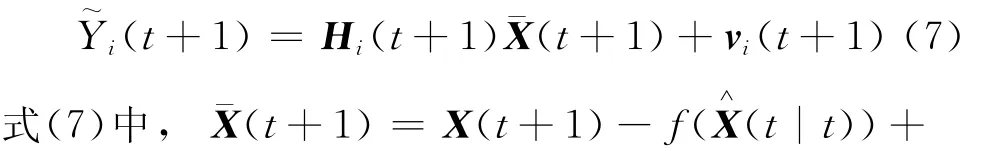
假設2：假設存在非奇異的矩陣

式中定義

2.2 基于貝葉斯估計的帶不同觀測矩陣的加權最小二乘分布式融合

在得到線性化的離散狀態方程和觀測方程后，為了提高觀測精度，可對式（10）的L個觀測方程進行觀測融合，對此本文采用基于Bayes估計的最小二乘方法對觀測方程進行觀測融合。

在對Kal man濾波觀測方程進行最小二乘觀測融合時，如果知道觀測值X（t＋1）的驗前信息，可以應用Bayes估計，得到基于Bayes估計的X－（t＋1）的估值表達式

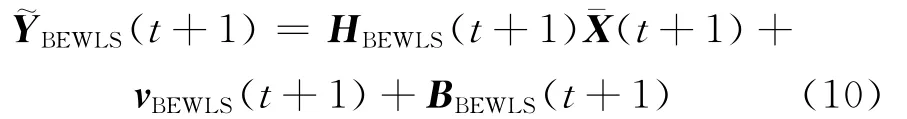
式中：

式（11）中，Y－BEWLS（t＋1）＝Y～BEWLS（t＋1）－BBEWLS（t＋1）。由RBEWLS（t＋1）＝E（v（t＋1）vT（t＋1）），可以求出高斯白噪聲vBEWLS（t＋1）的方差陣為

對式（6）和式（11）應用 Kal man濾波算法［3］可得基于Bayes估計的分布式觀測融合Kal man濾波器（t｜t）和預報器（t＋1｜t）及其相應的誤差方差陣MBEWLS（t＋1｜t）和MBEWLS（t＋1）。

3 比較與仿真

3.1 兩種加權最小二乘分布式融合卡爾曼濾波器算法的比較

為了說明本文提出的算法具有的優點，將本文的算法和文獻［5］提出的方法進行比較，文獻［5］提出基于WLS算法的分布式觀測融合Kal man濾波算法，其融合方程，即X－（t＋1）的估值表達式

式（12）中：

2)聯合制動系統是目前提高重載鉆機車復雜路況行駛安全的最有效辦法，該系統可承擔全部的低強度制動和大部分的正常制動，從而確保最大的安全性，幫助駕駛員獲得較高的平均駕駛速度從而縮短轉運周期。

WLS融合算法是無偏估計，但從統計決策的觀點來看，對于無偏的要求并不總是必要的，而可以用下列的概念來評價融合算法。

定義1：設Z為隨機向量，分布依賴與未知參數向量θ，記d（Y）為θ的一個估計，這里Y表示Z的樣本。記L［θ，d（Y）］為非負函數，它表示真實參數為θ，而以d（Y）作為它的估計時引起的損失，稱為損失函數。令

它表示真實參數為θ時，關于Y的分布所取的期望值。稱R（θ，d）為風險函數。如果對所有θ滿足

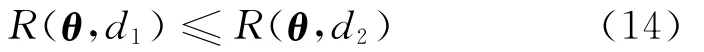
則稱估計d1至少和d2一樣好。如果

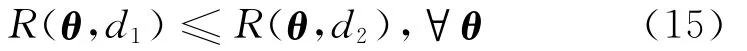
以及R（θ，d1）＜R（θ，d2）至少對某個θ成立，則稱d1優于d2。這個定義是對給定的損失函數而言的，常應用的是平方損失函數，即

此時

本文將風險函數作為評估估值好壞的標準，用它來評價BEWLS融合方法和WLS融合方法的優劣。

定理1：經過線性化的非線性離散多傳感器系統式（6）和式（7），在假設1—3的條件下，用BEWLS法所得到的分布式觀測融合Kal man濾波器優于用WLS法所得到的分布式觀測融合Kal man濾波器。

定理2：在假設2初值相同的條件下，即

存在

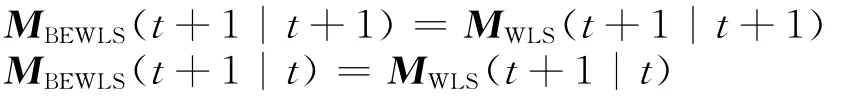
推論1：在假設2初值相同，即式（18）和式（19）成立的條件下

3.2 仿真實驗

本節將上節提出的BE WLS分布式融合Kal man濾波算法通過帶相關觀測噪聲和不同觀測矩陣的兩傳感器非線性跟蹤系統的例子來進行驗證和分析。考慮Kal man濾波系統i個傳感器觀測值（i，j＝1，2），用Tayl or級數線性化后，方程為：

式中，wi（t＋1）和vi，j（t＋1）是零均值的白噪聲隨機

式（23）—式（25）中有：

分別利用上面所述的兩種觀測融合Kal man濾波算法對多傳感器系統進行仿真計算，仿真時狀態的噪聲方差陣的值為C，觀測方程的噪聲方差陣的值為D，M（j）（0）為E 。

圖1和圖2為兩種融合算法的風險函數值，可以看出BEWLS融合算法的風險函數值在整個仿真時間段中都小于 WLS融合算法的風險函數值，將風險函數作為評估估值好壞的標準，說明BEWLS融合算法優于WLS算法。

圖1 兩種融合算法的風險函數值的比較（x 1（t＋1））Fig.1 Comparison of risk f unction values of t wo f usion algorit h ms（x 1（t＋1））

BE WLS融合算法是有偏差的，這種偏差是系統偏差，需要校正。本文依據多傳感器提供的測量和跟蹤信息，形成測量數據對，當采樣周期到時，利用已測量數據糾正系統偏差，補償和修正數據，實現多傳感器的融合跟蹤。圖3、圖4顯示用式（12）、式（13）校正BE WLS融合算法的結果，沒有校正前，出現了系統性的偏差，用式（12）來在線消除偏差，得到比較好的效果。

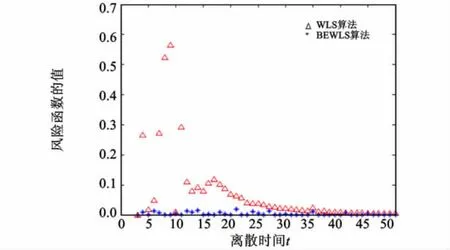
圖2 兩種融合算法的風險函數值的比較（x 2（t＋1））Fig.2 Co mparison of risk f unction values of t wo f usion algorithms（x 2（t＋1））

圖3 偏差對BEWLS融合算法的影響（x 1（t＋1））Fig.3 Bias effect on BEWLS f usion algorith m （x 1（t＋1））

圖4 偏差對BEWLS融合算法的影響（x 2（t＋1））Fig.4 Bias effect on BEWLS f usion algorith m （x 2（t＋1））

4 結論

本文提出了基于貝葉斯估計的帶不同觀測矩陣的加權最小二乘分布式融合Kal man濾波算法。該方法首先采用推廣的離散卡爾曼濾波對非線性系統線性化，然后在已知模型參數本身的先驗信息條件下，利用Beyes估計對Kal man濾波觀測方程進行觀測加權最小二乘融合。理論和仿真實驗證明BEWLS融合算法優于WLS算法，該算法具有以下特點：1）利用風險函數為評價指標，可以證明帶不同觀測矩陣的BEWLS分布式融合Kal man濾波算法優于WLS融合Kal man濾波算法，即采用BEWLS融合Kal man濾波算法能夠得到更高精度的融合數據；2）帶不同觀測矩陣的BEWLS融合Kal man濾波算法是有偏估計，但通過糾偏方法可消除融合偏差。

［1］歐連軍，丘紅專，張洪鉞.多個相關測量的融合算法及其最優性［J］.信息與控制，2005，34（6）：690-695.OU L J，QIU H Z，ZHANG H Y.Multiple correlated measurements f usion algorith m and its opti mality［J］.Inf or mation and Control，2005，34（6）：690-695.

［2］楊紅，羅飛，李艷，等.非線性離散系統的相關觀測融合時變 Kal man濾波［J］.控制與決策，2010，25（5）：669-675.YANG Hong，LUO Fei，LI Yan，etc.Correlated measurement f usion ti me-vary Kal man filtering algorith ms of nonliinear discrete system［J］.Control and Decision，2010，25（5）：669-675.

［3］鄧自立，高媛.按對角陣加權信息融合Kal man濾波器［J］.控制理論與應用，2005，22（6）：870-874.DENG Zili，GAO Yuan.Infor mation f usionin Kal m n filter weighted by diagonal matrices［J］.Control Theory ＆Applications，2005，22（6）：870-874.

［4］梁佐江，鄧自立.按三種不同加權準則的信息融合Kalman濾波器的性能比較［J］.黑龍江大學自然科學學報，2005，22（6）：789-792.LIANG Zuojiang，DENG Zili.Perf or mance co mparision of infor mation f usion Kal man filters weighted by three different ways［J］.Journal of Natural Science of Heilongjiang University，2005，22（6）：789-792.

［5］冉陳鍵，惠玉松，顧磊，等.相關觀測融合穩態Kal man濾波器及其最優性［J］.自動化學報，2008，34（3）：233-239.RAN ChenJian，HUI Yusong，GU Lei，et al.Correlated measurement f usion steady-state Kal mam filtering algorith ms and t heir opti mality［J］.Acta Ato mation Sinica，2008，34（3）：233-239.

［6］王松桂，史建紅，尹素菊，等.線性模型引論［M］.北京：科學出版社，2004.

［7］趙樹杰，趙建勛.信號檢測與估計理論［M］.北京：清華大學出版社，2004.

［8］張金槐.線性模型參數估計及其改進［M］.長沙：國防科技大學出版社，1999.