軌道車輛牽引電機負載模擬方法的研究

孫湖，陸峰，徐龍，楊中平

（北京交通大學 電氣工程學院，北京 100044）

1 引言

牽引電機負載模擬是軌道車輛牽引傳動系統半實物仿真中不可缺少的重要技術手段，其目的是為分析和研究牽引電機運行特性和性能、電傳動系統的控制方法獲取實驗室條件下的試驗數據，以克服真車試驗成本高、可行性低、外部條件改變困難以及試驗周期長等諸多缺點。牽引電機負載模擬技術在電機與變流器參數和容量選擇、牽引電機控制方法、空轉滑行再粘著控制、牽引網壓波動和直流側諧波影響等諸多與傳動系統相關的研究中都具有重要作用。

選擇牽引電機的負載轉矩作為模擬對象，是因為通過模擬負載的變化，不僅可以模擬列車運行的不同工況，同時可以模擬不同工況以及擾動作用下傳動系統中電流、電壓、頻率、轉矩等關鍵物理量的變化；控制相應的物理量按照期望的規律變化，就可以模擬車輛運行時傳動系統的實時控制，從而為改進復雜情況下牽引電機和變流器的控制方法提供依據。負載模擬得越準確，仿真系統就越能反映真車運行的實際情況；同時，只有準確地模擬電機負載，在此基礎上進行的傳動系統相關課題的研究才能夠深入開展。本文所探討的正是如何對軌道車輛牽引電機進行負載模擬的方法。

2 負載模擬原理

圖1是負載模擬系統的示意圖。本文所探討的負載模擬為電動負載模擬［1－4］，牽引電機與負載電機軸聯在一起，分別提供牽引轉矩和負載轉矩。負載轉矩中的慣性部分可以由負載電機提供，可以由飛輪裝置來模擬，也可以由負載電機和飛輪共同模擬。

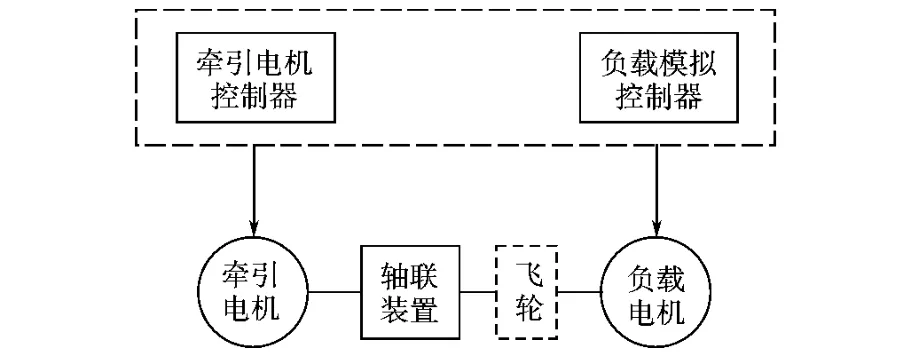
圖1 負載模擬系統示意圖Fig.1 The structure of load simulation system

軌道車輛牽引電機負載模擬，就是以負載電機轉矩的形式表現出牽引電機的實時負載轉矩，通過控制負載電機輸出轉矩為牽引電機加載，模擬牽引電機實際負載情況。負載電機可以是直流電機，也可以是交流電機。由于牽引電機的負載不僅和車輛運行狀態、參數以及線路條件等多種因素有關，而且是隨速度的變化而變化的，因此對于負載電機來講，就是要根據轉速信號和運行條件，快速準確地輸出同時符合運行阻力特性和車輛慣性的負載轉矩。

圖2為動力轉向架牽引電機與輪對傳動機構示意圖。該圖反映了牽引電機、傳動齒輪和輪對三者的作用關系。傳動齒輪位于齒輪箱中，通過傳動比將電機轉矩放大，轉速減小。整車重量通過轉向架上的懸掛裝置加在輪軸上，通過輪對作用于鋼軌。由于輪對承載后對軌道正壓力的作用，牽引電機輸出轉矩最終通過輪軌粘著產生車輛的整體牽引力或制動力，驅使車輛牽引或制動。

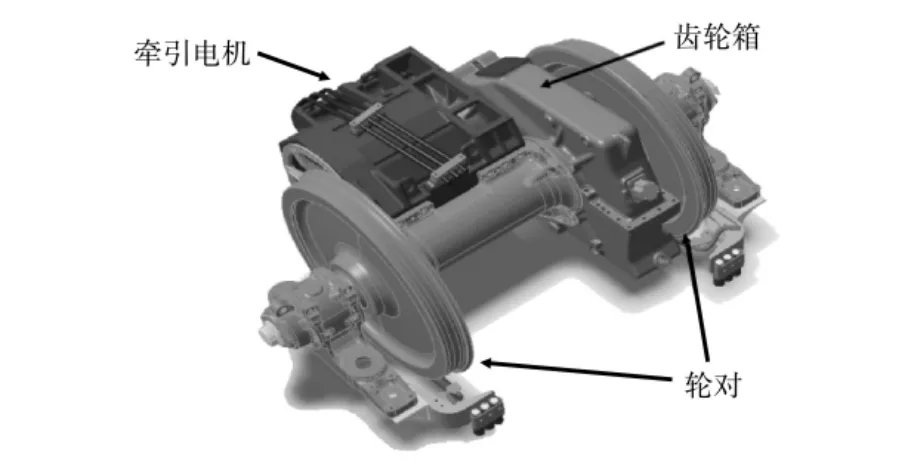
圖2 牽引電機與輪對傳動示意圖Fig.2 The structure of traction motor and wheel on transmission

在車輛實際運行中，電機負載的變化十分復雜，不僅要受到固有阻力和慣性質量的影響，而且會受到各種無法預測的隨機擾動的影響。然而，所有這些影響因素都可以最終轉化到牽引電機軸側，并以轉矩和轉動慣量的形式表現出來。這個轉化的過程，就是對牽引電機負載進行模擬等效的過程。負載模擬的最終目的，就是要使牽引電機作用在負載模擬系統與實際車輛上時具有同樣的外部響應特性。負載模擬的關鍵在于系統建模的準確性。

3 負載模擬系統建模

下面就從物理力學的基本原理出發，推導負載模擬系統的數學模型。

3.1 電機負載的力學推導

首先對動力傳動機構進行受力分析，如圖3所示。

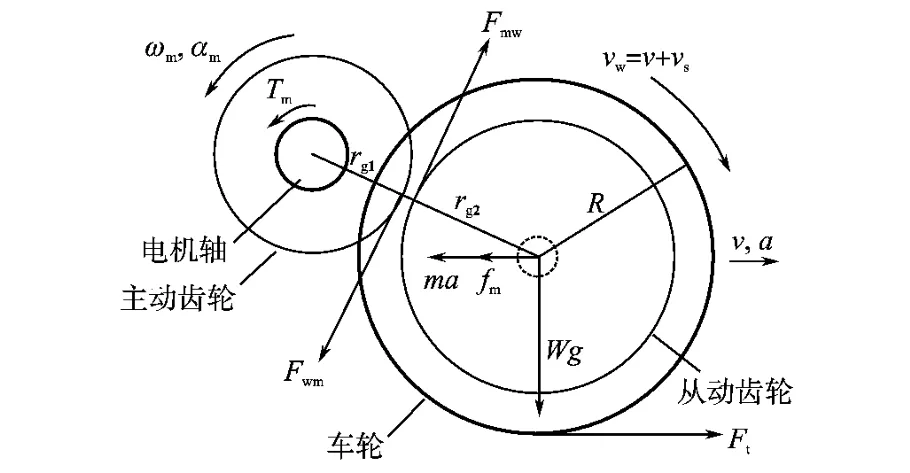
圖3 輪對受力分析Fig.3 Wheel to force analysis

圖3中，Tm為牽引電機輸出轉矩，N·m；ωm為牽引電機機械角速度，rad／s；αm為牽引電機機械角加速度，rad／s2；Fmw為電機通過主動齒輪對從動齒輪的作用力，N；Fwm為輪對通過從動齒輪對主動齒輪的作用力，N；Ft為單動軸輸出輪周牽引力，N；fm為單動軸分配阻力，N；m為單動軸分配質量，kg；W 為軸重，t；v為車輛直線運行速度，m／s；a為車輛直線加速度，m／s2；rg1為主動齒輪半徑，m；rg2為從動齒輪半徑，m；R為車輪半徑，m。

由牛頓力學第2定律，考慮列車運行時的整體受力情況，有

式中：F為編組總牽引力，N；f為車輛編組總阻力，N；M為編組總質量，kg。

為分析方便，本文針對單臺電機的情況進行受力分析。將上式等號兩端同時除以Nm，得到

這便是對單動軸列出的平動方程。

對輪對的定軸轉動列寫動力學方程：

式中：Jw為輪對與從動機構的轉動慣量之和，kg·m2。

考慮輪軌之間蠕滑現象的存在，應當有

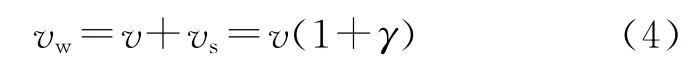
另有

式中：ωw為輪對角速度，rad／s；αw為輪對轉動角加速度，rad／s2；vw為輪對輪周線速度，m／s；vs為蠕滑速度，m／s；r為蠕滑率。

聯立式（2）～ 式（6），容易解出：

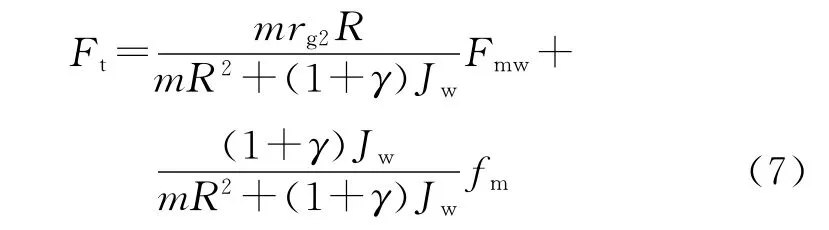
可見，Ft的大小不僅受到牽引電機輸出轉矩的影響、而且與列車質量和阻力的大小有關。實際運行中為了保證列車不發生空轉和滑行，應當控制Ft不超出最大粘著系數的限制，即：

式中：μ（vs）為計算粘著系數。

下面考慮電機實際負載轉矩TL。對于牽引電機，有下式成立：

式中：TL為電機實際負載轉矩，N·m；Jm為牽引電機與主動機構的轉動慣量之和，kg·m2。

考慮到齒輪傳動效率的影響，有（適用牽引工況，制動工況則乘以ηGear）：

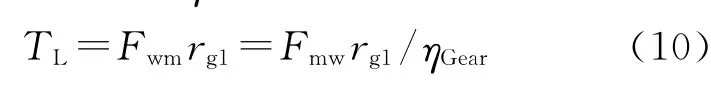
聯立式（2）、式（4）、式（6）、式（7）、式（10），并由傳動齒輪的傳動關系

得到：

式中：Nm為牽引電機（動軸）個數，Nm＝1；ig為齒輪傳動比；ηGear為齒輪傳動效率。

式（12）就是牽引電機實際負載轉矩的表達式。

3.2 電機負載的功率推導

以下從動能定理出發列寫功率方程，同樣來求解牽引電機實際負載。

系統平動的功率方程為

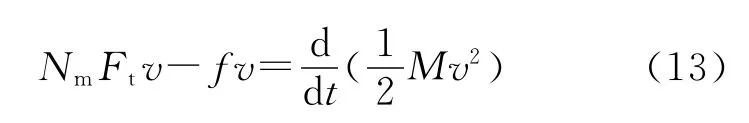
牽引電機轉動的功率方程為

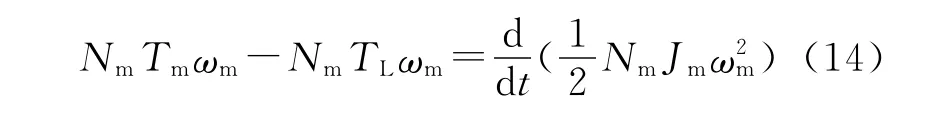
動力輪對轉動的功率方程為

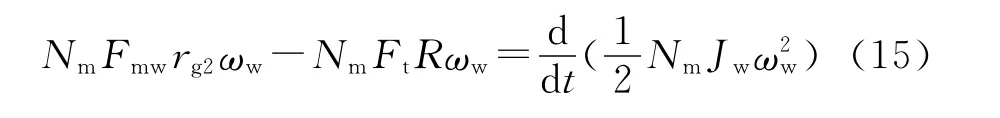
以上3式相加，結合式（10），得到：

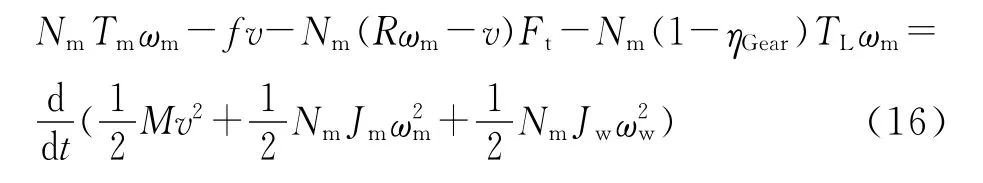
式（16）左邊第3項意味著輪周牽引力由于輪周速度高于車輛前進速度而做了功。在不考慮輪軌接觸面發生相對滑動的情況下，這部分功實際上轉變為輪對和鋼軌的形變勢能，這部分勢能被等效地包含在了等式右側動力輪對的轉動動能中。左邊第4項則是由于齒輪傳動效率小于1造成的功率損失。

另外需要說明的是，式（16）中并未包括拖車輪對的轉動動能，因而該方程并不是整個編組的功率方程。在等式左右兩端分別加上從動輪輪軌摩擦力做功功率和從動輪動能的微分，便可得到全列車的總功率方程。由于從動輪對的受力并不影響牽引電機，編組總功率方程不再在此列出。

將式（2）、式（4）、式（6）、式（9）、式（11）代入式（16）并將微分項展開，得到

顯然，式（17）就是式（12）。這也說明，從功率的角度和從力的角度推導的結果完全一致。

3.3 等效阻力負載與等效慣性負載

將式（17）代入式（9），得到：

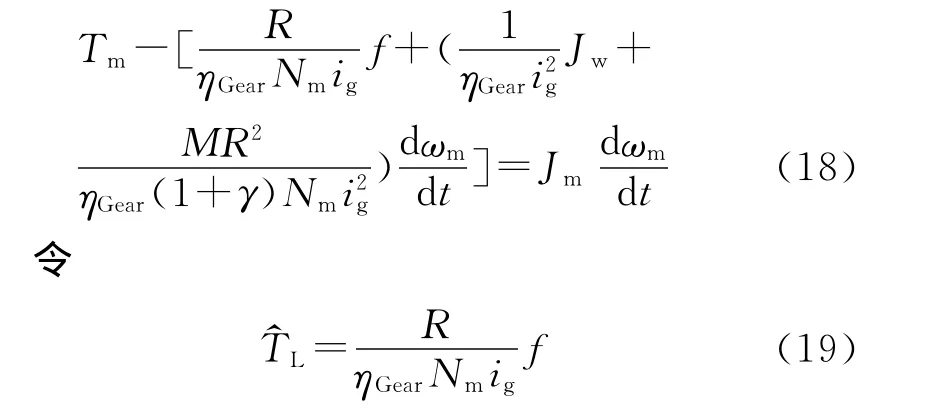
將式（18）寫成如下形式：

式（19）中，f指的是包括了基本運行阻力和坡道阻力、隧道阻力、曲線阻力等各種附加阻力在內的總阻力。于是就代表了由全部阻力引起的電機負載，稱為等效阻力負載轉矩；J＾就是包括了編組質量和傳動機構的轉動慣量在內的負載等效轉動慣量（dωm／dt）則代表了由慣性質量引起的電機負載，稱為等效慣性負載轉矩。

于是，可以提出這樣一種負載模擬方法：由負載電機的輸出轉矩模擬等效阻力負載，由負載電機的輸出轉矩或者具有大慣量的機械裝置（如飛輪）模擬等效慣性負載。這樣，實際負載被等效為主動施加到牽引電機軸側的可控轉矩，從而實現了牽引電機的負載模擬。

4 實車參數驗證

為了驗證上述結果的正確性和準確性，結合CRH2型動車組的實車參數及牽引特性曲線對該方法進行驗證。

圖4為牽引特性曲線，車輛實際的參數［5］為：M＝408.5t，JW＝80kg·m2，R＝0.41m，Jm＝6 kg·m2，Nm＝16，ηGear＝0.95，ig＝3.036。

圖4 CRH2型動車組牽引性能曲線Fig.4 Train traction performance curves CRH2type

基本阻力經驗公式（其中v的單位為km／h）：

fb＝8.63＋0.07295v＋0.00112v2（N／t）

若按照平直道上車輛運行狀況進行驗證，則取式（19）中f＝fbM／1000，蠕滑率γ的取值與圖4一致。

按照上文中提到的“牽引電機作用在負載模擬系統與實際車輛上時具有同樣的外部響應特性”原則，若給定牽引轉矩與圖4一致，且給定負載轉矩與式（21）一致，如果負載模擬建模準確，則牽引電機角加速度應當與圖4一致。但是，從圖4中直接觀察加速度的取值比較困難，采用上述思路的等效方法則可以更加直觀，即：若給定電機角加速度與圖4一致，且給定負載轉矩與式（21）一致，如果負載模擬建模準確，則由式（21）得到的牽引轉矩應當與圖4牽引轉矩相同。于是，把實際參數代入式（19）、式（20），并將計算得到的電機牽引轉矩推導值T＾m與圖4中的實際值Tm比較，結果如圖5所示。

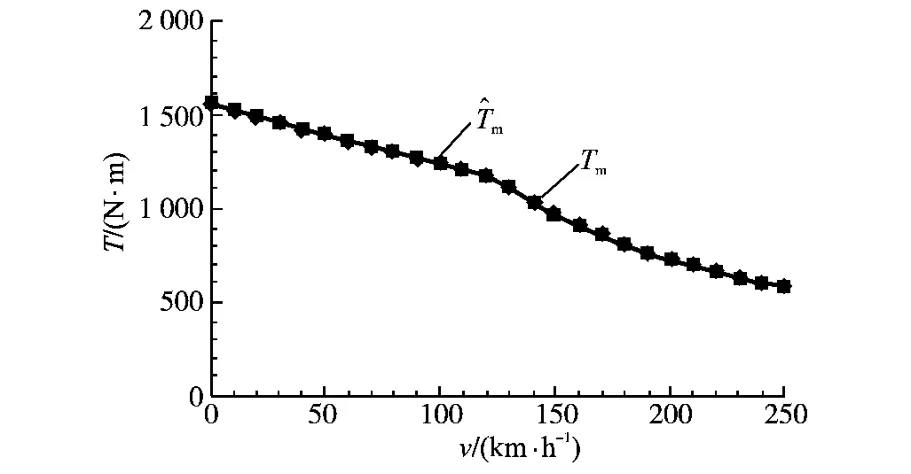
圖5 實際牽引轉矩與推導轉矩Fig.5 The actual traction torque and derivation torque

由圖5可以看出，牽引轉矩的推導值曲線與實際曲線基本吻合。表1顯示了圖5中主要速度點的實際轉矩、推導轉矩及其誤差數據。

表1 牽引轉矩校驗結果Tab.1 Examine results of traction torque

可見，在全速域范圍內，推導轉矩的最大誤差約13N·m，相對誤差不到1%。

表1中顯示推導轉矩的數值仍略小于實際值。此時的誤差主要是由牽引計算中使用的“慣性系數”［5－6］與式（20）等效的慣性系數不完全相等引起的。在牽引計算中，牽引力由下式得到：

式中：β為牽引計算使用的慣性系數。

由式（21）聯立式（19）并結合圖4中牽引力與電機牽引轉矩的關系，容易得到

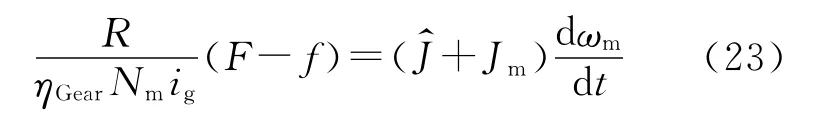
結合式（22）及a與ωm的關系，可以得到J＾的另一種表達式：

將式（24）代入式（21）得到的牽引轉矩與圖4牽引轉矩是完全相同的。因此，如果將式（20）再乘以一個修正系數α，則可以實現推導轉矩與牽引轉矩的完全一致。此修正系數可以由式（24）除以式（20）得到，其表達式為

圖4采用的慣性系數為0.04，代入式（25）解得此修正系數約為1.0085。將式（20）乘以1.0085后再求推導轉矩，結果與實際牽引轉矩在舍入誤差范圍內完全一致。

上述驗證結果表明，負載模擬系統建模是正確的，也是準確的。

5 負載模擬系統仿真

圖6所示為基于CRH2型動車組參數的牽引電機負載模擬系統仿真結構圖。該系統由負載電機提供阻力負載，由飛輪模擬全部慣性負載。牽引系統輸入量為等效阻力負載轉矩，輸出量為轉速；負載系統輸入量為轉速，輸出量為等效阻力負載轉矩。牽引電機參數設置包含了飛輪慣量，其給定轉矩與圖4牽引轉矩相同；負載電機轉矩與轉速關系滿足式（19）確立的關系。電機都采用間接矢量控制方式。

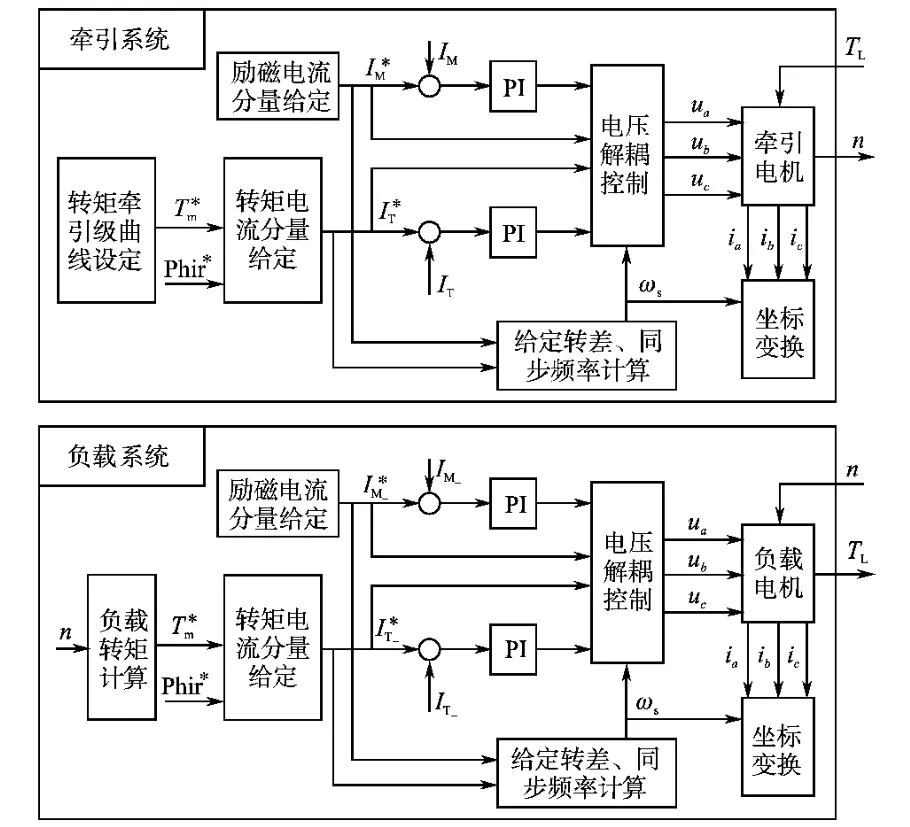
圖6 負載模擬系統仿真結構圖Fig.6 Load simulation system simulation structure

牽引電機為三相鼠籠式異步電機，額定功率300kW，額定電壓2000V，額定頻率140Hz，定子電阻0.144Ω，定子漏感1.4mH，轉子電阻0.146Ω，轉子漏感1.3mH，激磁電感32.8mH，負載電機參數與牽引電機相同。負載等效轉動慣量（修正后）計算值為497kg·m2。

系統仿真結果見圖7。啟動牽引轉矩約1560 N·m（對應啟動牽引力176kN，見圖4），平直道上阻尼轉矩由啟動時的31N·m（對應阻力3.49 kN）上升至250km／h時的343N·m（對應阻力38.6kN）。啟動加速度0.411m／s2和250km／h時的剩余加速度0.060m／s2都略高于實際值（對應分別為0.406m／s2和0.059m／s2）。結果表明，牽引電機在實際牽引轉矩和模擬負載轉矩共同作用下，其加速性能與實際加速性能基本一致。啟動加速度和最高運行速度下的加速度相對誤差都能控制在2%以內，如果考慮到仿真步長、PI參數和系統延遲的影響，這樣的誤差范圍在工程實踐中是可以接受的。

6 結論

本文從力學和功率的角度推導得到一致的電機負載模型，都說明了對負載轉矩的控制包括兩個方面：一個是非線性的阻力負載轉矩，另一個是帶有微分運算環節的慣性負載轉矩。前一種系統是最簡單的非線性系統，控制相對簡單；后一種系統由于采用了機械負載的逆動力學模型，其微分項在離散控制系統中不僅容易帶來噪聲干擾，而且極易引起系統的不穩定。因此，對慣性負載的控制是系統控制的難點。

采用飛輪模擬慣性負載的方法可以大大降低控制的難度，但同時會造成實驗裝置體積和重量的增加；飛輪慣量難以改變的特性也會限制實驗平臺功能的發揮，降低負載模擬的靈活性。因此，如何使用飛輪來模擬慣性負載是搭建實驗平臺之前必須解決的關鍵問題。另外，負載模擬系統中牽引電機、負載電機與變頻器的參數和容量如何匹配、如何提高負載響應的快速性和準確性等問題，也需要在今后的研究中逐步加以解決。本文提出的負載模擬方法為進一步的研究提供了基本理論依據，后續工作將圍繞上述問題深入展開。

［1］李宗帥，董春.國外基于電動技術的機械負載模擬的現狀［J］.機械，2007，34（5）：1－3.

［2］王明彥.電動負載模擬技術的研究［D］.哈爾濱：哈爾濱工業大學，2004.

［3］Padilla A J，Asher M G，Sumner M.Control of an AC Dynamometer for Dynamic Emulation of Mechanical Loads with Stiff and Flexible Shafts［J］.IEEE Transactions on Industrial Electronics，2006，53（4）：1250－1260.

［4］Rodic M，Jezernik K，Trlep M.Control Design in Mechatronic Systems Using Dynamic Emulation of Mechanical Loads［C］∥IEEE ISIE 2005.Croatia：Dubrovnik，2005：1635－1640.

［5］張曙光.CRH2型動車組（中國高速鐵路技術叢書／和諧號CRH動車組技術系列）［M］.北京：中國鐵道出版社，2008.

［6］邵興.理論力學［M］.北京：清華大學出版社，2009.