稠密柵元不同子通道內湍流流動的RANS和URANS模擬

于意奇，顧漢洋，楊燕華，程 旭

（上海交通大學 核科學與工程系，上海 200240）

稠密柵元的燃料組件廣泛應用于先進的反應堆設計。因稠密的柵元結構將減少水鈾比從而硬化了中子能譜，這將提高轉換比并增加燃料利用率［1－3］。

最早的棒束內的湍流流動實驗研究開始于20世紀60年代。近年來，隨著實驗測量手段的發展，越來越多的實驗研究開始關注于棒束內的湍流流動［4－9］。

實驗研究表明:棒束內的湍流流動和圓管內的完全不同，在棒束間隙區有很強的交混。這一現象曾被歸結于二次流，不過，最近的實驗研究表明這并不是影響棒束間強交混的主要因素。棒束間隙區的準周期流動振動才是影響子通道間能量質量交換的最主要因素。這種流動振動和子通道的幾何構造與雷諾數密切相關，當雷諾數低于一定的臨界值時，這種振動便消失［10］。實驗發現，壁面通道中，在1.015≤W／D≤1.250（W 為棒最遠端距壁面的距離，D為棒徑）的范圍內，流動振動的頻率隨間隙的減小而減小［11］。盡管對這一流動振動現象還未完全了解，但學術界普遍認為這是由于流動的不穩定造成的。

如今，RANS、LES、URANS和 DNS方法均被應用于模擬棒束內的湍流流動［12－16］。研究表明:采用各向同性的湍流模型的穩態模擬（RANS）無法再現棒束流動的強各向異性的特點。盡管采用各向異性的湍流模型的穩態模擬可模擬出湍流驅動的二次流現象，但在P／D（P為兩棒之間的中心距離）較小的稠密柵元子通道內，二次流不是影響流動的主要因素。所以，在這些子通道中，模擬的結果往往與實驗有一定的差距。盡管數值模擬粗略高估了振動的波長，URANS方法對稠密柵元棒束間隙的流動振動有較好的模擬結果。

在這些方法中，DNS方法是最理想的一種，因為對于整體的流動振動現象還不是十分了解。LES方法幾乎可得到和DNS相同的結果。但由于LES和DNS的計算代價太大，URANS是目前比較實際的一種數值模擬方法。

1 數值方式

在本研究中，將選用不同P／D和通道形狀的子通道實驗作為參考。詳細的實驗參數和數值模擬信息列于表1［4，17－18］。實驗截面圖示于圖1。

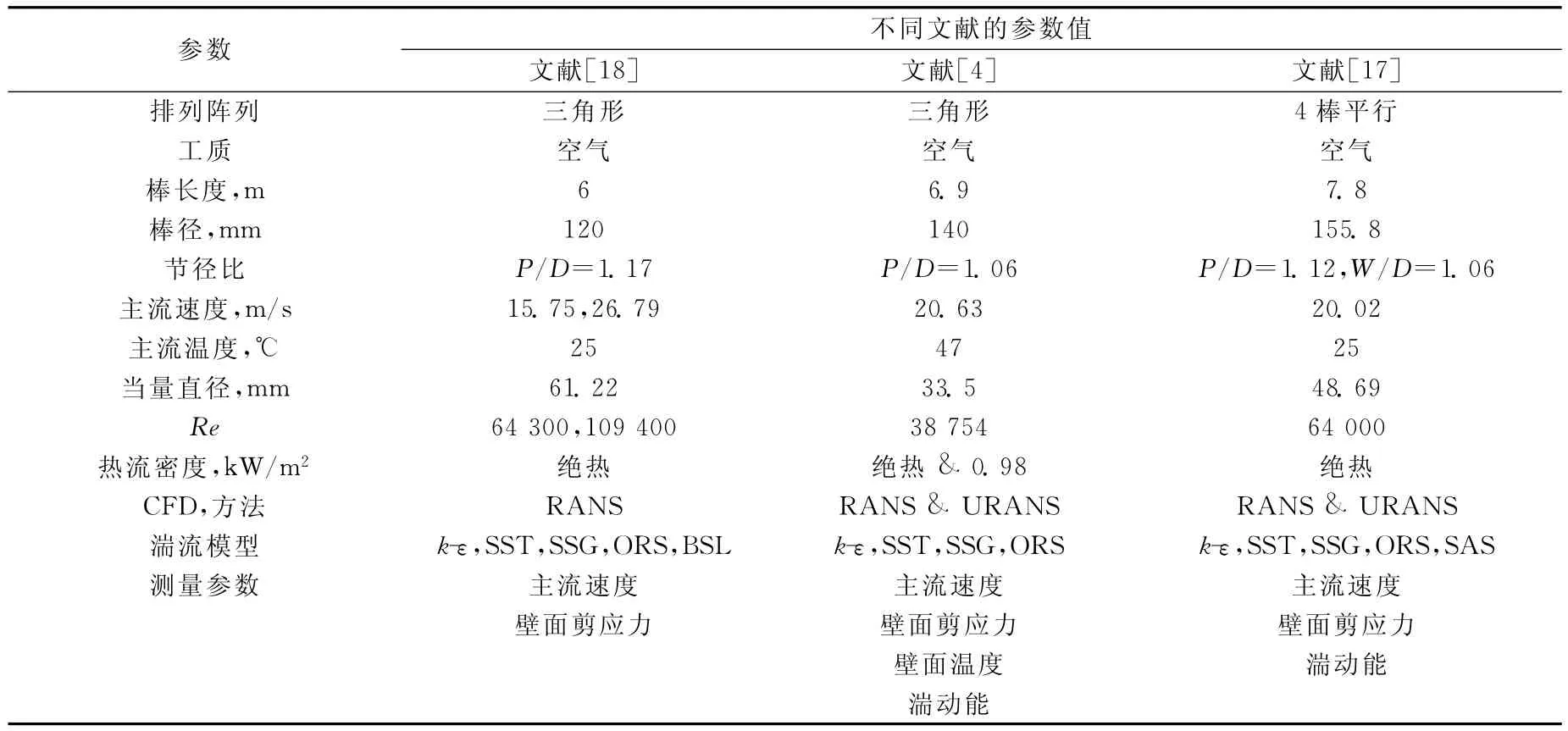
表1 本工作的實驗和數值參數Table 1 Experimental and numerical parameters

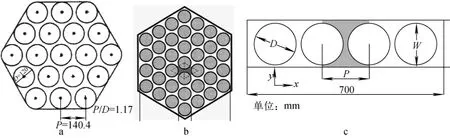
圖1 實驗截面圖Fig.1 Set－up cross－section

1.1 RANS模擬

由于子通道的對稱性，選用1／6和1／4子通道作為RANS模擬的計算域，如圖2所示。棒、通道和表面采用非滑移的邊界條件，進口采用均流的邊界條件，出口設置定壓的邊界條件，其余為對稱的邊界條件。通過網格敏感性分析，分別得到25萬的中心子通道網格和50萬的壁面子通道網格。采用渦粘性和雷諾應力模型來評估它們對于稠密柵元內湍流模擬的適用性。渦粘性模型包括k－ε模型和SST模型，雷諾應力模型包括ORS、SSG和BSL模型。所有模型均采用壁面函數模擬近壁面的流動。所有近壁面網格保持y＋＝1。

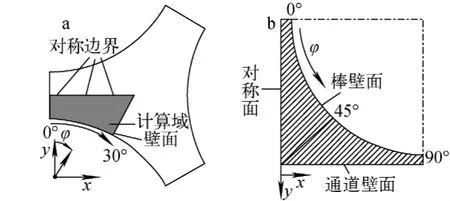
圖2 RANS的計算域Fig.2 Computational domain for RANS

1.2 URANS模擬

URANS計算域包括兩個由間隙連接的子通道（圖3）。整個計算包括3組周期性邊界條件和非滑移的壁面邊界條件。進出口的周期性邊界條件固定質量流速，計算長度為0.6m（4倍于實驗測量的平均波長λ）。

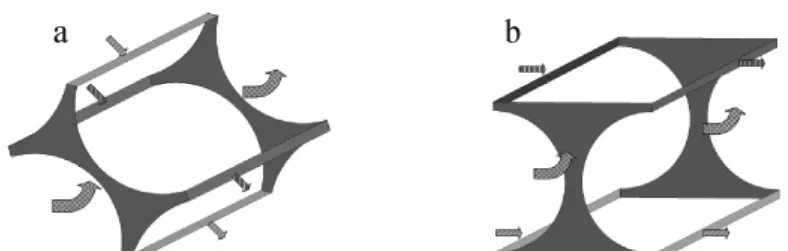
圖3 URANS的計算域Fig.3 Computational domain for URANS

網格總數為60萬，時間步長滿足:Δt?1／f，f為最小振動頻率，Δt選為10－4s。幾乎所有應用于RANS模擬的湍流模型均被應用于URANS計算。另外，專為瞬態模擬設計的SAS湍流模型也將應用于URANS計算。

2 結果和討論

本工作對所有工況均進行了RANS模擬，對P／D＝1.06的三角形排列的中心通道和4棒束平行排列的子通道進行了URANS計算，并將主流速度、壁面剪應力、湍動能和壁面溫度等參數與文獻［4］的實驗結果進行比較。

2.1 主流速度

對于P／D為＝1.17的三角形排列子通道，RANS模擬計算結果示于圖4。圖中，y為徑向上與壁面距離，v為主流速度。棒束內的二次流雖尺度很小，但它將影響子通道內的湍流分布。雷諾應力模型將湍流的各向異性考慮在內，所以，雷諾應力湍流模型（BSL，ORS，SSG）較渦粘性湍流模型（k－ε，SST）得到的速度分布更接近實驗測量結果。由圖3b可見，SSG湍流模型的模擬計算結果與實驗測量結果吻合良好。

P／D＝1.06的三角形排列稠密柵子通道內的速度分布示于圖5。圖中，Wb為主流速度，ymax為徑向上速度最大值與壁面的距離。在棒束間隙區（φ＝30°），RANS和 URANS的計算結果有很大差異，其原因在于棒束間隙區存在強烈的速度振動。在URANS的計算結果中，各向異性的SSG湍流模型給出了對實驗更好的預測。4棒平行排列稠密柵元子通道的速度分布示于圖6。由圖6同樣發現，在棒束間隙區，URANS的結果較RANS有很大改進。

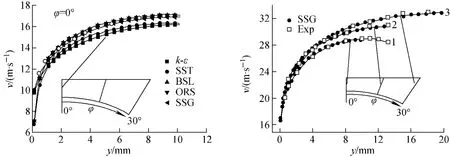
圖4 P／D＝1.17的三角形排列子通道主流速度分布Fig.4 Velocity distributions in triangular array with P／D＝1.17

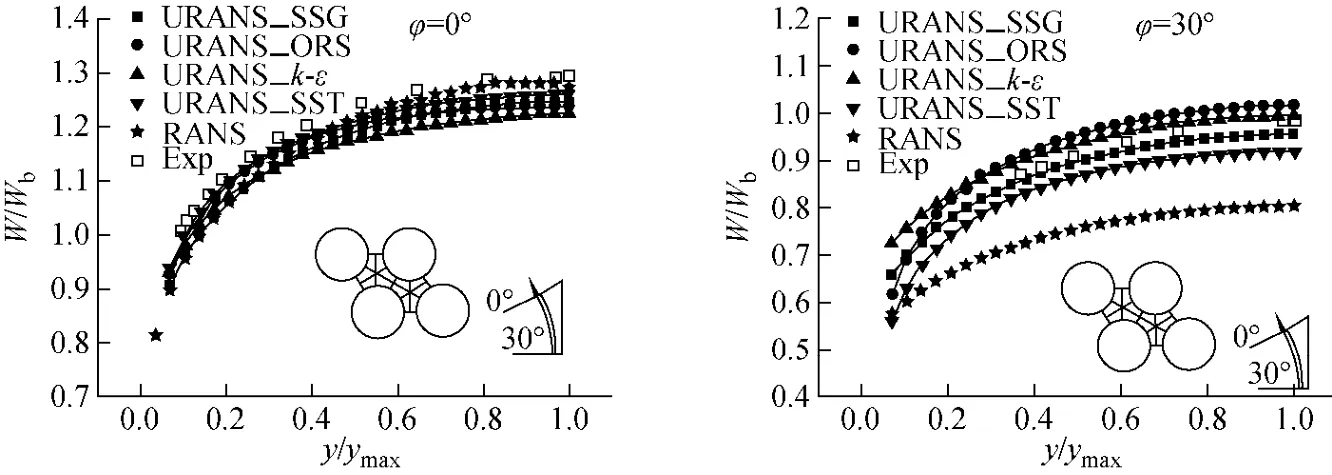
圖5 P／D＝1.06的三角形排列稠密柵子通道內速度分布Fig.5 Velocity distributions in triangular array with P／D＝1.06

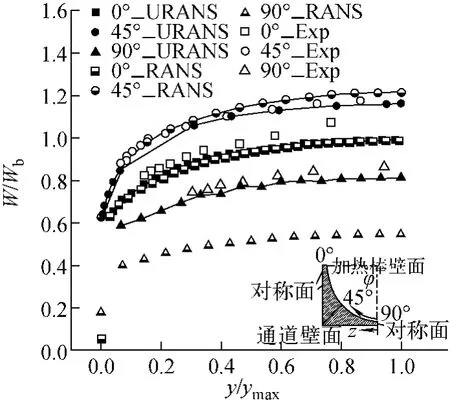
圖6 P／D＝1.12、W／D＝1.06的4棒束平行排列子通道速度分布Fig.6 Velocity distributions in 4rod parallel array with P／D＝1.12，W／D＝1.06

2.2 壁面剪應力

圖7示出P／D＝1.17的三角形排列子通道內的壁面剪應力tau的分布。圖中，taum為壁面平均剪應力。圖7a顯示，雷諾應力湍流模型（SSG、BSL、ORS）的模擬結果更為平坦，較渦粘性湍流模型（k－ε、SST）也更接近實驗結果。這是由于雷諾應力湍流模型對二次流的模擬均化了壁面剪應力的分布。圖7b示出了雷諾數更高的情況，模擬結果同樣證實了上述結論。

圖8示出P／D＝1.06的三角形排列子通道內的壁面剪應力分布。由圖8可見，在URANS計算方式下，即便采用各向同性的k－ε湍流模型，得到的結果也比在RANS計算方式下采用SSG湍流模型得到的結果更接近實驗測量結果。這也證明了在P／D較小的稠密柵元子通道中，二次流不再是主導的影響因素。

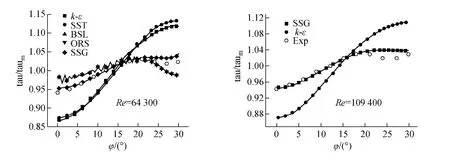
圖7 P／D＝1.17的三角形排列子通道內的壁面剪應力分布Fig.7 Wall shear stress distributions in triangular array with P／D＝1.17

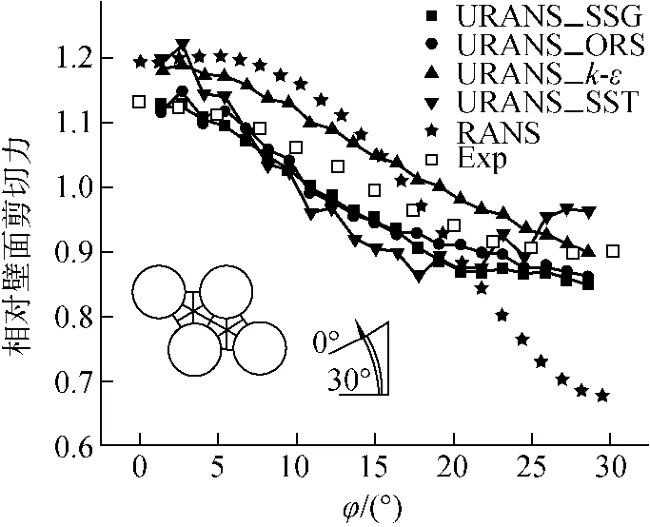
圖8 P／D＝1.06的三角形排列子通道內壁面剪應力分布Fig.8 Wall shear stress distributions in triangular array with P／D＝1.06

同樣，在URANS計算方式下，雷諾應力湍流模型（SSG、ORS）的模擬結果較渦粘性湍流模型（k－ε、SST）更接近實驗測量結果。

URANS同樣得到更為均化的壁面通道壁面剪應力的分布（圖9），并與實驗吻和良好。在RANS計算中，只有各向異性的湍流模型可模擬出二次流。而在URANS計算中，流動的對稱性被打破，在短時間平均下無法觀察到二次流，但在足夠長的時間下采用雷諾平均，即使采用各向同性的湍流模型也能重現二次流。

2.3 湍動能

稠密柵間隙區的流動振動是一種相干結構，在比較湍動能時，有必要把這種流動振動貢獻考慮在內。通常，相對湍動能的定義如下:

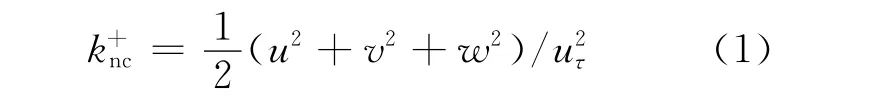
式中:u、v、w分別為軸向速度波動、徑向速度波動和周向速度波動；uτ為壁面剪應力；k＋nc為湍動能的非相干部分。由速度振動引起的湍動能稱為湍動能的相干部分k＋c，其定義如下:

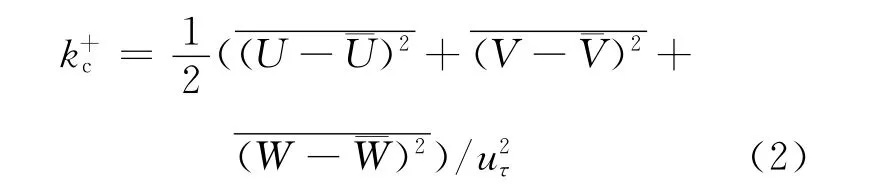
總湍動能為兩部分之和:

圖10示出三角形排列和4棒束平行排列的子通道在不同周向角度上的湍動能分布。由圖10可見，URANS的計算精確性高于RANS。專門為非穩態計算設計的SAS湍流模型較其他湍流模型有著更高的模擬精度。

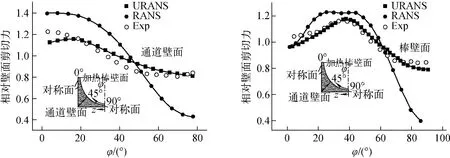
圖9 P／D＝1.12、W／D＝1.06的4棒束平行排列子通道壁面剪應力分布Fig.9 Wall shear stress distributions in 4rod parallel array with P／D＝1.12，W／D＝1.06

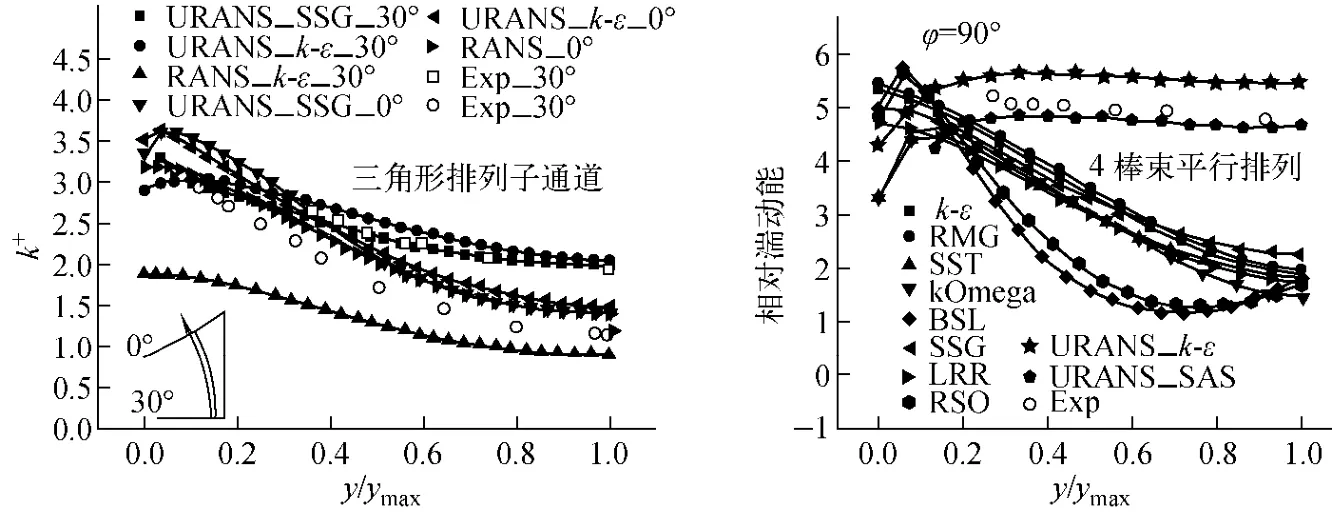
圖10 稠密柵元子通道湍動能分布Fig.10 Turbulent intensity distributions in tight lattice

2.4 壁面溫度

圖11示出P／D＝1.06的三角形排列子通道壁面溫度分布，溫度通過平均溫度來進行無量綱化處理。由圖11可見，URANS的模擬結果更為均化并與實驗測量結果吻合良好。因此，稠密柵元內的流動振動均化了壁面溫度，對于反應堆堆芯的工業設計是有利的。

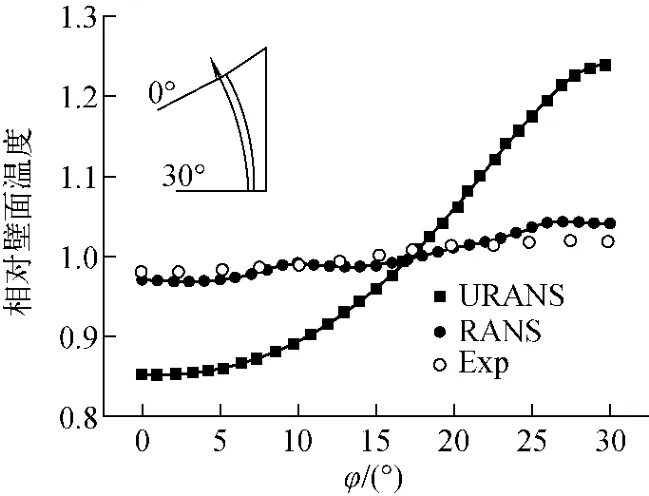
圖11 P／D＝1.06的三角形排列子通道壁面溫度分布Fig.11 Wall temperature distributions in triangular array with P／D＝1.06

2.5 流動振動

稠密柵元子通道內的流動振動緩慢發展，最后發展為穩定的波動（波幅達到常值或準常值）。圖12示出三角形排列子通道窄縫區的橫向速度隨時間的變化和三維振動快照。振動幅度為2m／s，與文獻［4］的實驗測量結果相近。然而，計算所得振動波長比實驗測量結果大。

總體而言，URANS仍無法模擬稠密柵元內相干結構的所有特性，但對于正確預測主流速度、壁面剪應力和壁面溫度等工業關心的統計變量十分實用。

3 結論

本工作對典型的子通道（中心通道和壁面通道）進行URANS和RANS計算。計算結果表明，在較寬的稠密柵元通道（P／D＝1.17）內，采用SSG湍流模型的RANS計算能很好地再現實驗結果。對于P／D較小（P／D＜1.1）的稠密柵元子通道，窄縫區內大尺度的流動振動將顯著影響子通道的湍流流動。URANS模擬雖無法再現稠密柵元子通道內流動振動的所有動力特性，但可很好地預測子通道內的主流速度、壁面剪應力、湍動能分布。推薦采用SAS和SSG湍流模型進行URANS計算。

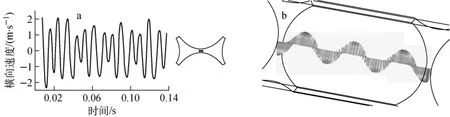
圖12 P／D＝1.06的三角形排列子通道窄縫區橫向速度波動（a）和三維流動振動快照（b）Fig.12 Flow pulsation（a）and dimension snapshot of oscillation（b）in narrow gap in triangular array subchannel with P／D＝1.06

［1］OLDEKOP W，BERGER H D，ZEGGEL W.General features of advanced pressurized water reactors with improved fuel utilization［J］.Nuclear Technology，1982，59:212－227.

［2］UCHIKAWA S，OKUBO T，KUGO T，et al.Investigations on innovative water reactor for flexible fuel cycle（LFWR）［C］∥Proceedings of GLOBAL.Tsukuba，Japan:［s.n.］，2005.

［3］CHENG X，LIU X J，YANG Y H.A mixed core for supercritical water－cooled reactors［J］.Nuclear Engineering and Technology，2008，40（1）:1－10.

［4］KRAUSS T，MEYER T.Experimental investigation of turbulent transport of momentum and energy in a heated rod bundle［J］.Nuclear Engineering and Design，1998，180:185－206.

［5］TRUPP A C，AZAD R S.The structure of turbulent flow in triangular array rod bundles［J］.Nuclear Engineering and Design，1975，32:47－84.

［6］TRIPPE G，WEINBERG D.Non－isotropic eddy viscosities in turbulent flow through rod bundles［M］∥Turbulent Forced Convection in Channels and Bundles:Vol.1.KAKAC S，SPALDING D B.Washington:Hemisphere Publishing Corporation，1979:505.

［7］SEALE W J.Turbulent diffusion of heat between connected flow passages［J］.Nuclear Engineering and Design，1979，54:183－195.

［8］REHME K.Simple method of predicting friction factors of turbulent flow in non－circular channels［J］.International Journal of Heat and Mass Transfer，1973，16:933－950.

［9］REHME K.The structure of turbulent flow through rod bundles［J］.Nuclear Engineering and Design，1987，99:141－154.

［10］MEYER L，REHME K.Large－scale turbulence phenomena in compound rectangular channels［J］.Experimental Thermal and Fluid Science，1994，8:286－304.

［11］BARATTO F，BAILEY S C C，TAVOULARIS S.Measurements of frequencies and spatial correlations of coherent structures in rod bundle flows［J］.Nuclear Engineering and Design，2006，236:1 830－1 837.

［12］BAGLIETTO E，NINOKATA H.Turbulence models evaluation for heat transfer simulation in tight lattice fuel bundles［C］∥Proceedings of the 10th International Topical Meeting on Nuclear Reactor Thermal Hydraulics （NURETH－10）.Seoul，Korea:［s.n.］，2003.

［13］CHANG D，TAVOULARIS S.Unsteady numerical simulations of turbulence and coherent structures in axial flow near a narrow gap［J］.ASME Journal of Fluids Engineering，2005，127（3）:458－466.

［14］CHANG D，TAVOULARIS S.Numerical simulation of turbulent flow in a 37－rod bundle［J］.Nuclear Engineering and Design，2007，237:575－590.

［15］MERZARI E，NINOKATA H，BAGLIETTO E.Large eddy simulation of the vortex street between rectangular channels［C］∥NTHAS 5.Jeju Island，Korea:［s.n.］，2006.

［16］NINOKATA H，MERZARI E，KHAKIM A.Analysis of low Reynolds number turbulent flow phenomena in nuclear fuel pin subassemblies of tight lattice configuration［J］.Nuclear Engineering and Design，2009，239（5）:855－866.

［17］KRAUSS T.Experimentelle untersuchung des turbulenten w?rme－und impulstransports in einem beheizten stabbündel ［R］.Germany:Karlsruhe University，1996.

［18］MANTLIK F，HEINA J，CHERVENKA J.Results of local measurements of hydraulic characteristic in triangular pin bundle，UJV－3778－R［R］.Rzez，Czech Republic:［s.n.］，1976.