軟土區抗拔樁荷載—位移曲線歸一化數值分析★

魏 杰 李校兵 盧永洪

隨著我國國民經濟的日益發展，高層和超高層建筑不斷涌現，基礎埋置越來越深。沿海地區土地資源有限，地下空間的開發利用越來越廣，地下結構的建設呈現迅猛發展的勢頭(如:地下車庫、下沉式廣場、地下商場、地下通道、江底隧道、地鐵等)。由于我國沿海地區地下水位較高，地下建筑物通常需要承受巨大的浮力。當地下水浮力一旦超過結構物重量及側壁摩擦力時則上浮隨之發生，建筑物將產生變形等破壞。地下結構物的抗浮問題成為影響結構工程設計和工程投資效益的難題之一，并日益受到國內外學者的重視。

張潔(2005)［1］研究上拔力作用點位置對抗拔樁變形的影響。劉文白(2004)［2］采用顆粒流理論數值模擬了砂土地基樁的上拔試驗，對各級荷載下樁的上拔位移及土顆粒的分布、速度和位移進行了分析，并根據顆粒流數值模擬的荷載—位移曲線確定了極限上拔荷載和極限上拔位移，其曲線特征與物理實物試驗的荷載—位移曲線基本一致。

黃鋒(1999)［3］對砂土中的抗拔樁位移變形進行了分析，采用樁周土變形模式反映樁基荷載傳遞規律，推導出抗拔樁荷載—位移關系的理論解，同時，黃鋒還對土的剪脹性對樁側摩阻力的影響做了簡化模型分析，得出了剪脹性對抗拔樁和承壓樁側摩阻力的不同影響。Kulhawy(1979)［4］發現等截面抗拔樁基礎主要破壞形態為沿著樁—土界面上發生圓柱形剪切破壞。李森和唐孟雄［5］對抗拔樁荷載—位移曲線的模型進行了比較分析，得到冪函數、指數函數、雙曲線函數擬合的效果對比。Hsiung和 Chen(1997)［6］提出了荷載—位移曲線歸一化分析方法，該方法思路是通過歸一化參數將樁的荷載—位移曲線歸一為單一曲線，得到圖表方便工程應用。

本文在孫曉立等［7］的研究基礎上進一步探討抗拔樁荷載—位移曲線的歸一化分析方法，利用搜集到的軟土地區抗拔樁工程實測數據作為對比，選擇合適的標準化的參數將荷載和位移轉換成無量綱的量，從而擬合為單一曲線。最后通過回歸分析，建立該曲線的回歸公式。該公式對實際工程中抗拔樁設計和施工具有一定的參考價值和工程意義。

1 工程實測數據

筆者搜集了溫州軟土地區許多規模比較大的工程建設項目的抗拔樁工程實測數據，現選擇其中兩個工程項目加以簡要說明。

1． 1 溫州置信廣場

該工程位于溫州市飛霞南路與錦繡路交叉口西南側，場地面積36 246 m2，地上總建筑141 305 m2。建筑物主要由A，B，C樓及地下室組成，A，C樓超高層建筑采用圓筒—剪力墻結構，B樓采用框架結構。該工程對5根樁(試樁12，17～20)進行單樁抗拔實驗了解其荷載—上拔性狀。根據工程現場靜載實驗得到的抗拔樁工程實測數據如表1所示。

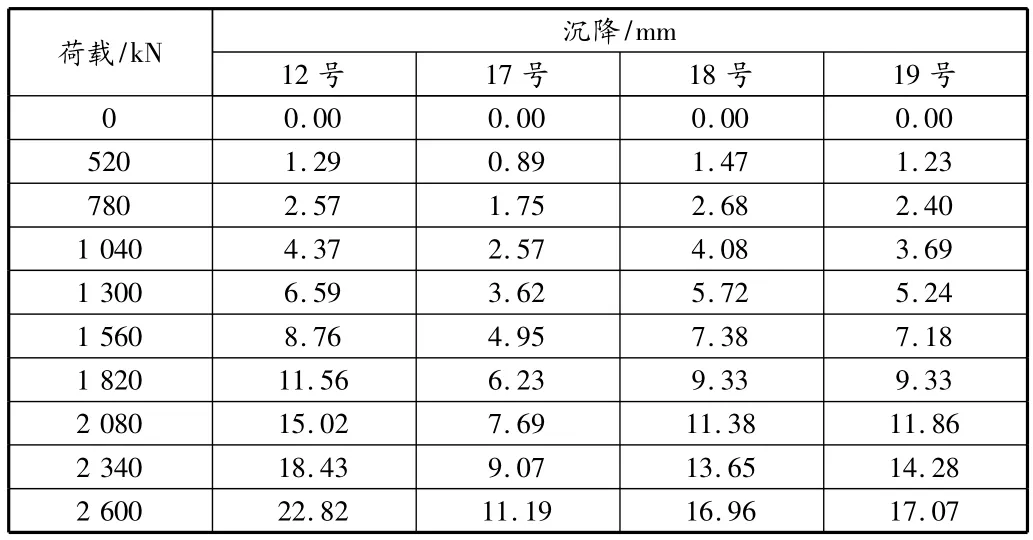
表1 溫州置信廣場抗拔樁工程實測數據表

1． 2 溫州東海廣場

該工程位于溫州市城市中心區西南部，東北靠市府大道，東南為劃龍河，西為站東路。工程總征地面積25 198 m2。該工程對4根實驗樁進行單樁豎向抗拔靜載試驗，以了解其承載能力及荷載—上拔性狀。根據工程現場靜載實驗得到的抗拔樁工程實測數據如表2所示。

表2 溫州東海廣場抗拔樁工程實測數據表

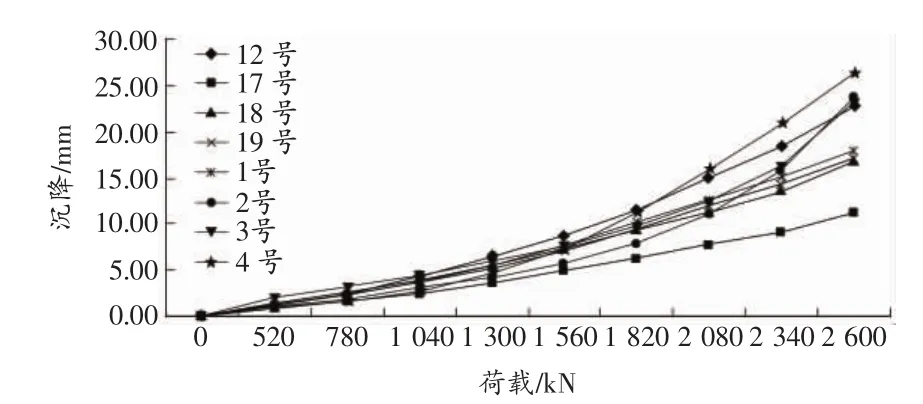
圖1 抗拔樁工程荷載—位移曲線

2 抗拔樁歸一化數值分析

2． 1 抗拔樁荷載—位移曲線

為了給出具有代表性的抗拔樁荷載—位移曲線族并且減少分析的工作量，選取了具有代表性的樁和土的參數(見表3)。

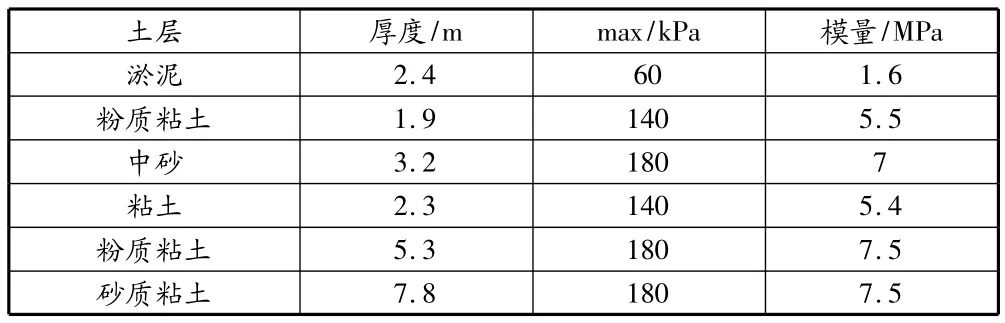
表3 各土層的物理力學參數

抗拔樁1號～4號的樁徑為600 mm，樁長66 m，樁周混凝土強度為C35，持力層為卵石層。鋼筋配筋情況:主筋為16φ20，箍筋為φ6@250螺旋筋，加強箍為φ12@2 000。

2． 2 歸一化標準參數的確定

我們知道在沒有任何規律的抗拔樁荷載—位移曲線中，要準確地推導出它們之間的關系是困難的，為此我們并不單獨的討論每一個影響條件對抗拔樁承載力的影響，而是選擇合適的標準化參數將荷載和位移轉換成無量綱的量，再討論它們之間的關系。

筆者選擇了土體的屈服強度ωmax為標準化位移參數，而對應的抗拔樁的理論承載力為標準化荷載參數。

Randolph［8］通過理論推導給出土體屈服位移的理論公式:

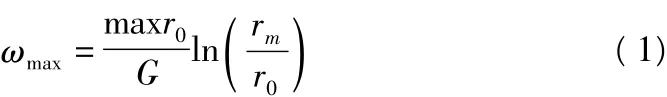
其中，G為土體剪切模量;r0為樁的半徑;rm為樁的影響半徑。

孫曉立［7］通過理論推導又得出歸一化的抗拔樁荷載和土體位移的理論公式:

其中，Ep為樁體彈性模量;Ap為樁的截面面積;L為樁長。

工程實測數據的歸一化分析計算參數見表4。

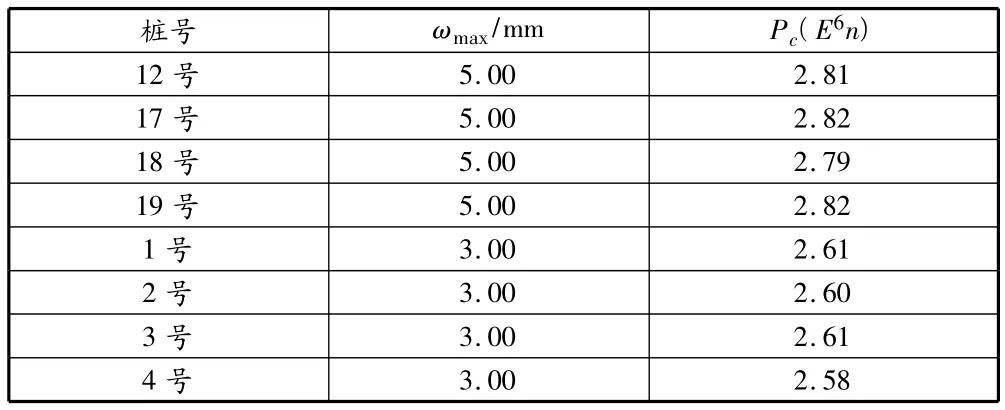
表4 抗拔樁歸一化分析的計算參數

由圖2可以看出，通過標準化參數將原本沒有規律的荷載位移曲線基本聚集在一起。

2． 3 回歸公式的確定

通過以上研究，將抗拔樁的荷載—位移曲線歸一化為單一曲線。為了更方便的預測和計算給定變形條件下的抗拔樁承載力，我們運用最小二乘法，用數學公式來擬合該曲線。通過Matlab的計算與分析，筆者嘗試通過多項式函數、雙曲線函數和指數函數擬合該曲線，均取得較好的擬合效果。由于多項式函數表現形式比較簡單，采用多項式函數擬合歸一化曲線，擬合方程為:

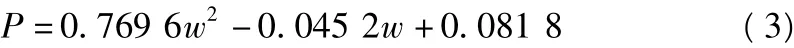
其中，P為無量綱荷載，為樁體承受的荷載與土體屈服對應荷載之比;w為無量綱變形值，為樁體的上拔位移和土體屈服位移之比。

即有:

通過以上分析，給出的歸一化曲線公式使得預測抗拔樁的承載能力變得簡單方便。

圖2 抗拔樁荷載—位移曲線最終歸一化曲線

2． 4 回歸公式的驗證

通過標準化荷載參數和標準化變形參數將抗拔樁荷載—位移曲線歸一擬合出來，并得到了一個相對準確簡潔的計算公式，在避免了繁瑣的數值分析的同時還為抗拔樁工程設計提供了參考。

為了驗證回歸公式的正確性，筆者將擬合后的公式代入原來的點族中，歸一化公式的曲線與實測數據的對比如圖3所示。

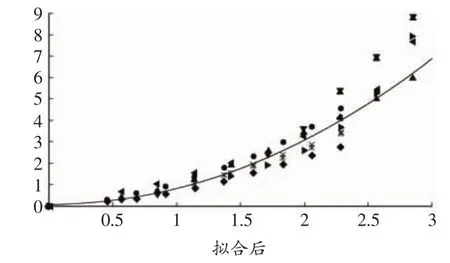
圖3 歸一化公式曲線與實測數據對比

由圖3可以看到實測數據均勻地分布在擬合曲線的兩側而且非常接近，證明了所得公式的正確性。

3 結語

1)通過選擇適當的標準化參數，將抗拔樁荷載—位移曲線族歸一化為單一曲線是可行的，本文通過對軟土地區抗拔樁工程實測數據分析和處理，得到了以溫州為代表的軟土地區抗拔樁荷載—位移歸一化函數。該函數在確定樁體位移的前提下能夠較為準確的預測出抗拔樁的承載能力。對工程及設計有一定的參考價值。2)任取8組抗拔樁實測數據驗證歸一化回歸公式的正確性，結果表明，回歸公式的預測歸一化曲線和工程實測非常接近，證明了該回歸公式的有效性，采用歸一化公式可以很好的預測抗拔樁的樁頂變形，理論預測結果和實測結果比較接近，說明該方法具有較高的實用價值和工程意義。

［1］ 張 潔，尚岳全，林旭武．考慮上拔力作用點位置影響的抗拔樁變形分析［J］．土木工程學報，2005，38(7):102-106．

［2］ 劉文白，周 鍵．上拔作用下樁的顆粒流數值模擬［J］．巖土工程學報，2004，26(4):516-521．

［3］ 黃 鋒，李廣信，呂 禾．砂土中抗拔樁位移變形的分析［J］．土木工程學報，1999，32(1):31-36．

［4］ Fred H．Kulhawy，David W．Kozera．Uplift testing of model drilled shafts in sand［J］．Journal of the Geotechnical Engineering Division，1979，105(1):31-47．

［5］ 李 森，唐孟雄．抗拔樁荷載—位移曲線擬合模型的比較分析［J］．地下空間與工程學報，2009，5(4):56-58．

［6］ Hsiung YM，Chen YL．Simplified method for analyzing laterally loaded single piles in clay［J］．Journal of Geotechnical and Geoenvironmental Engineering，1997，123(11):1018-1029．

［7］ 孫曉立，莫海鴻，楊 敏．抗拔樁荷載—位移曲線的歸一化［J］．華南理工大學學報，2008，36(11):33-34．

［8］ Randolph MF，Dolwin J，Beck R．Design of driven piles in sand［J］．Geotechnique，1994，44(3):47-48．