把握概念本質 建構生態課堂——對初中數學概念課教學的幾點思考

312400 嵊州愛德外國語學校 閭 煒

數學概念是人類對現實世界的空間形式和數量關系的簡明概括及反映，它是數學學科的精髓、靈魂.數學概念是進行推理、判斷、證明的依據，是建立定理、法則、公式的基礎，也是形成數學思想方法的出發點.因此，概念教學在數學教學中有著重要的地位和作用.對數學概念的教學，其“生態課堂”的建構一定要以學生已有的認知基礎為出發點，去創設能讓學生經歷概念的發生、發展過程的教學情境.本文從學生認知基礎的角度出發，就概念教學中的課堂建構作簡單討論.

1 把握概念的本質

1.1 內涵和外延

任何一個概念都有它明確的內涵和外延.內涵是指概念所反映的事物的本質屬性，通常是通過下定義的方法來表示的，如“函數”的定義是“在某一變化過程中，有兩個變量x，y.在某一法則的作用下，如果對于x的每一個值，y都有唯一的值與其相對應，這時，就稱y是x的函數.”函數概念的本質：兩個變量之間的一種特殊的對應關系.“函數”不是一個數，而是一個對應關系.

外延是指概念所涉及的范圍和條件.如“函數”的外延是“在某一變化過程中”，即函數概念所反映的基本思想是運動變化的思想.

1.2 客觀和抽象

概念是從客觀事物中概括和抽象出來的，它反映了客觀事物的本質屬性和內在聯系，因此，具有客觀性.一個概念能夠反映出大量形形色色的物質的共同屬性，因而具有高度的概括性和抽象性，它超脫了具體的現象而說明了事物的本質.

1.3 發展和變化

概念是在科學實踐中逐步形成和發展起來的，一個概念的內涵是否正確，外延是否恰當都要用實踐來檢驗，并隨著科學實踐的深入發展而不斷得到補充、修正和重構.

1.4 聯系和結構

概念和概念之間雖然可以進行精確的區分，但它們之間并不是孤立的，它們之間存在著直接的或間接的聯系，其主要形式是從屬和并列.如四邊形是個大概念，平行四邊形是個小概念，正方形是個更小的概念，但正方形的四邊相等、四角相等、對角形互相垂直平分且相等的共同屬性，就比四邊形的共同屬性四條邊、四個角要更多些.

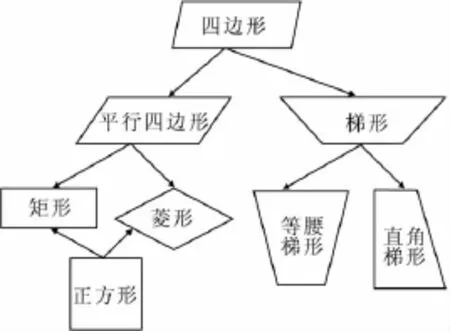
圖1

2 概念教學中“生態課堂”的建構的方法

2.1 重視導入，激發思維

數學教學情境的創設，是指在數學教學中對教學內容的呈現采用特定的方法，來達到激發學生主動地聯想、想象、積極地思維，以獲得某種與新學內容有關的形象或思維成果.在教學時，要根據學生的實際來創設具有啟發性的、能激發學生求知欲望的問題情境，使學生用自己的思維方式積極思考、主動探索、創新數學知識.

2.1.1 利用學生在日常生活中熟悉的具體事例進行引入

通過貼近學生的生活實例，來對相應的概念作出解釋，使學生從感性認識到理性認識，有利于學生加深對概念的理解.

如：筆者在認識函數(1)時的情境引入：

問題1國家發改委通知，自10月26日零時起，將汽油、柴油的價格上調，上調后的93#汽油零售價為6.53元/升，如果設加油量為x升，應付的金額為y元，你能完成下表嗎?

加油量x(升) 1 5 10 15 20 … x …應付金額y(元)

然后回答下列問題：(1)在上述變化過程中，有幾個變量?

(2)再給定一個x值，你還能求出相應的y的值嗎?

(3)當加油量確定時，應付金額能確定嗎?

(4)你能用含x的代數式表示y的值嗎?

問題210月26日滬杭高鐵正式投入運營，上海至杭州全長202千米，列車從上海到杭州所需的時間為t小時，列車行駛的平均速度為v千米/小時.

(1)在這個變化過程中，有幾個變量?

(2)怎么用含v的代數式表示t?

(3)當v=303，350時，你能求出相應的t的值嗎?(保留2個有效數字)

(4)再給定一個v值，你還能求出相應的t的值嗎?

2.1.2 在舊概念的基礎上通過對比、類比引入新概念

又如：在反比例函數的圖象和性質的引入部分，此教學設計是類比了正比例函數的圖象和性質，先讓學生回顧正比例函數的圖象和性質，并列出表格，列出解析式、形狀、位置、圖象趨勢、增減性等，接下來類比這些內容研究反比例函數的圖象和性質.

2.2 剖析概念，揭示本質

數學概念是用精練的數學語言表達出來的，在教學中，抽象概括出概念后，還要注意深入剖析概念的定義，幫助學生進一步理解概念的含義.

例如，在學習函數概念時：

(1)“在某個過程中，有兩個變量x和y”是說明：變量的存在性與函數是研究兩個變量之間的依存關系.

(2)“對于在某一范圍內的每一個確定的值”是說明變量x是在一定范圍內取值，即允許值范圍也就是函數的定義域.

(3)“y有唯一確定的值和它對應”說明有唯一確定的對應規律.

(4)“y是x的函數”揭示了誰是誰的函數，由以上剖析可知，函數概念的本質是變量之間的關系.筆者在上認識函數時是這樣剖析函數概念的.

第一步：通過上面兩個引例，叫學生回答：這些變化過程中，兩個變量之間的關系有什么共同點?(在變化過程中，一個量確定，另一個變量也隨之唯一確定).

母親也納悶兒，這糧食哪來的，問父親，父親也不講。母親生氣了，問，是偷來的嗎，這事可不能做，寧愿挨餓，也不能干那事啊！父親大怒，說母親侮辱他，告訴母親這是用汗水掙來的，干凈著呢，放心吃吧。

第二步：按學生回答和引例得出函數概念.教師板書并講解函數的概念要點：變化過程中;兩個變量(x，y);x每一個確定的值，y都有唯一確定的值(x叫做自變量，y是x的函數).

第三步：概念辨析：判斷下列說法是否正確?為什么?(1)在圓的面積公式S=r2中，S與r之間構成函數關系.(2)已知每支鋼筆5元，要買x支鋼筆的總價為y元，那么y是x的函數.

第四步：觀察生活中所遇到的或者熟悉的某些變化過程是否存在函數關系，讓學生嘗試用兩個變量來描述.

第五步：在學生回答的基礎上教師再補充

如：中國2010年上海世博會園區即時客流統計圖.

第六步：探究函數關系的表示方法：在前面學生已經接觸到的幾個函數，教師引導學生歸納總結：

在問題1中，金額y與加油量x的關系y=6.53x.用等式來表示函數關系的方法叫解析法.

如問題2門票張數a(張)與金額b(元)的關系

門票張數(張) 1 3 5 10 20 … t …金額b(元) 160 480 800 1600 3200 … 160t …

把自變量的值和函數對應值列成一個表，這種方法叫列表法.

中國2010年上海世博會園區即時客流統計圖：用圖象來表示函數關系的方法，叫圖象法.

函數概念的得出由學生嘗試完成，經過上一環節三個問題的分析，學生體驗了函數的發現歷程，基本上能夠把握住函數概念的關鍵點.通過學生自己的歸納總結，讓學生經歷批判和相互推翻的過程，最終由學生將關鍵點串聯，形成與教材接近的函數概念.這樣，學生對函數內涵的印象會深刻.

2.3 抓住重點，深化內涵

揭示概念的內涵不僅由概念的定義完成，還常常由定義所推演的一些定理、公式得到進一步理解.如以三角函數的定義為基礎，推導特殊角的三角函數值，以及解直角三角形，可使學生清楚地看到概念是學習其它知識的依據.反過來又會使三角函數的內涵得到深入揭示，加深對概念的理解，增強運用概念進行推理判斷的思維能力.筆者在教學生解直角三角形時是這樣深化三角函數內涵的.

選題如圖，京杭運河修建過程中，某村考慮到安全性，決定將運河邊一河埠頭的臺階進行改造.在如圖的臺階橫斷面中，將坡面AB的坡角由45°減至30°.已知原坡面的長為6cm.(BD所在地面為水平面)

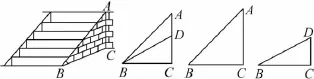
(1)改造后的臺階坡面會縮短多少?

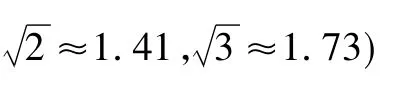
解決這類問題的關鍵是要回歸三角函數定義，找準找對解題所需要的直角三角形.先讓學生找出這題目中的直角三角形.然后根據已知條件AB=6cm和三角函數定義在直角三角形ABC中求出AC和BC的長，再利用三角函數定義和BC的長求出BD和CD的長，那么這個題目的答案就找到了.

2.4 歸納總結，區分異同

“有比較才有鑒別”，數學的各種知識要讓學生在比較中去思考、去認識.數學的一些概念和規律，理論性較強而且比較抽象，如果把它與學生熟悉的(已知的)相關實體(事物)進行比較，從中理解概念、掌握規律，學生就會對它產生極大興趣，就會主動思考.如關于“軸對稱圖形”和“軸對稱”這兩個概念學生較難理解，但通過讓學生觀察常見的汽車標志，如奔馳、大眾、桑塔那;商標如工行、農行等，看到它們共同的性質：沿某條直線翻折，左右兩邊能夠完全重合，這樣就容易理解軸對稱概念.

2.5 梳理概念，融匯貫通

數學中的概念，有些是互相聯系的，互相影響的，教學完一個單元或一章后，要善于引導學生把有關概念串起來，充分揭示它們之間的內部規律和聯系，從而使學生對所學概念有個全面、系統的理解，例如：初中函數從一次函數到反比例函數，再到二次函數，最后是三角函數.學習函數時都是從特殊到一般，從圖象到性質，再從性質到應用.

2.6 運用概念，形成系統

概念的形成是一個由個別到一般的過程，而概念的運用則是一個由一般到個別的過程，它們是學生掌握概念的兩個階段.通過運用概念解決實際問題，可以加深、豐富和鞏固學生對數學概念的掌握，并且在概念運用過程中也有利于培養學生思維的深刻性、靈活性、敏捷性、批判性和獨創性等等，同時也有利于培養學生的實踐能力.

運用概念的方法可以是①復述概念或根據概念填空.②運用概念進行判斷.③運用概念進行推理.

教學時，應闡明概念之間的內在聯系，明確概念的從屬關系，科學地、系統地分析概念的相互關系，如四邊形認知圖式的構建，把四邊形(平行四邊形、矩形、菱形、正方形等)的知識有機地融合在一起.