基于聲場計算的管道曲率對焊縫二次波檢測的影響

張益成,李曉紅,丁 輝

(武漢大學動力與機械學院,武漢 430072)

用超聲波對中厚壁管焊縫進行檢測,已被認為是一種行之有效的檢測方法,但對于小徑管焊縫檢測存在一定的困難,尤其體現在缺陷的定量方面。圖1(a)和(b)顯示了相同聲程的條件下,一次波檢測過程中聲波直接由反射體返回;二次波檢測過程中聲波經過了管內壁兩次散射,不同管內壁曲率對聲束的散射將導致反射體回波信號的不同。

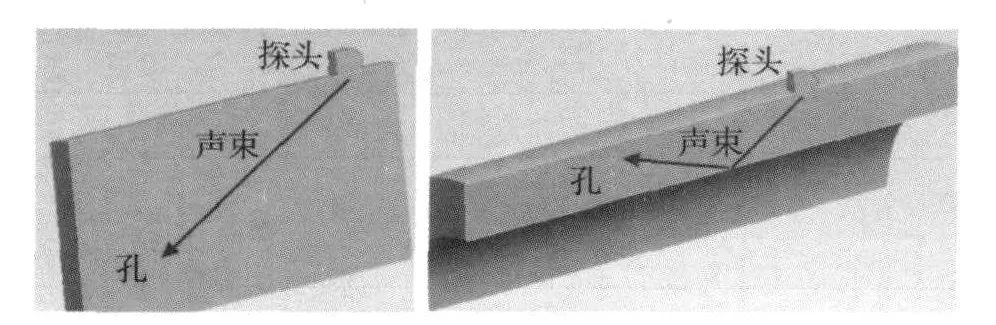
圖1 一次波與二次波檢測示意圖圖

國內外已開發多種仿真系統作為超聲檢測過程分析研究的重要手段[1-3],較好地解決了實驗研究當中只能以有限種類的規則反射體做回波信號分析,無法制作出其他種類的反射體(如球孔)的困難。筆者采用文獻[4]建立的超聲檢測計算分析系統UT-CAS,進行聲場和缺陷的回波計算。

1 計算模型與聲場計算

1.1 UT-CAS計算模型

UT-CAS的聲場計算模型是基于瑞利積分和pencil法建立的,計算時需要考慮如何將發射源與計算區域分別離散,并求解出相應的聲束路徑;分別計算各源點與計算點間的幅值、相位的變化,通過疊加所有源點的聲壓得到最終的聲壓分布。

聲束在圓柱曲界面的反射聲場計算時,反射路徑的求解是關鍵。筆者采用二分法求解反射路徑。根據pencil法的計算要求,路徑求解問題可以轉化為以下問題：假設半徑為r的圓柱體軸線與空間坐標系中的y軸重合,已知源點坐標為(x1,y1,z1)和計算點坐標為(x2,y2,z2),求解曲界面上反射點(x3,y3,z3)。在各向同性介質中,入射聲束向量、反射聲束向量及反射點上的法向量共面。因此對應任一個y值,都有且只有唯一點能滿足共面的要求,即是在y1,y2之間的每一個y值都只對應一個點,使得三個向量共面。同時斯涅爾定律還要求入射角與反射角相等,因此可以采用二分法不斷逼近唯一的反射點。

UT-CAS對于不同種類的缺陷采用不同的近似處理,根據實際檢測,本文計算用到的是裂紋回波模型。該模型適用于裂紋類缺陷和體積類缺陷(不含夾雜),采用基爾霍夫近似(Kirchhoff)[5]的高頻近似,忽略了表示沿缺陷表面傳播的瑞利波的二次衍射項,從而以衍射系數的形式給出散射場遠場振幅和入射場的關系。

1.2 管內壁反射聲場的計算與分析

發射聲場的計算作為回波信號計算的第一步是有必要的,對于管道焊縫的二次波反射法檢測,聲束在管道內壁反射后的聲場計算則是關鍵。用斜探頭分別檢測鋼板和三種不同尺寸的管道,分別計算聲束在鋼板底面和各管道內壁的反射聲場,并作對比分析。檢測所采用的斜探頭參數均為：晶片尺寸6 mm×6 mm,入射角 70°,中心頻率 5MHz。鋼板與管道的材質均為鐵素體鋼,其中鋼板厚度為10 mm,1,2和3號管道的內徑依次為φ40,60和80mm,管道壁厚均為10mm。鋼板底面的反射聲場和1號管道內壁反射聲場如圖2所示。其中橫坐標表示聲束軸線的相對位置,0值點為聲束在界面上反射點;縱坐標表示聲束的徑向位置,聲束軸線處于20 mm處。由圖2可見,管道內壁的反射聲束有明顯的散射,這是因為反射點偏離軸線,使得單一聲束的傳播距離增加。

比較各反射聲場的軸向聲壓和徑向聲壓,結果見圖 3。圖3(a)可見,四條曲線幾乎重合,說明反射面的曲率對軸線聲壓的影響極小。圖3(b)與(c)的對比結果可知：距離反射點近的區域,軸線附近聲壓大且趨于一致;而遠離反射點的區域,聲壓迅速下降,且聲壓隨曲率和距離的增加而發散增大。圖3(b)中距軸線3 mm處差值為0.5 dB;距軸線8 mm處差值達5.5 dB;圖3(c)中距軸線3 mm處差值為0.3 dB;距軸線8 mm處差值為 3.8 dB,距軸線10 mm處差值達6.6 dB。

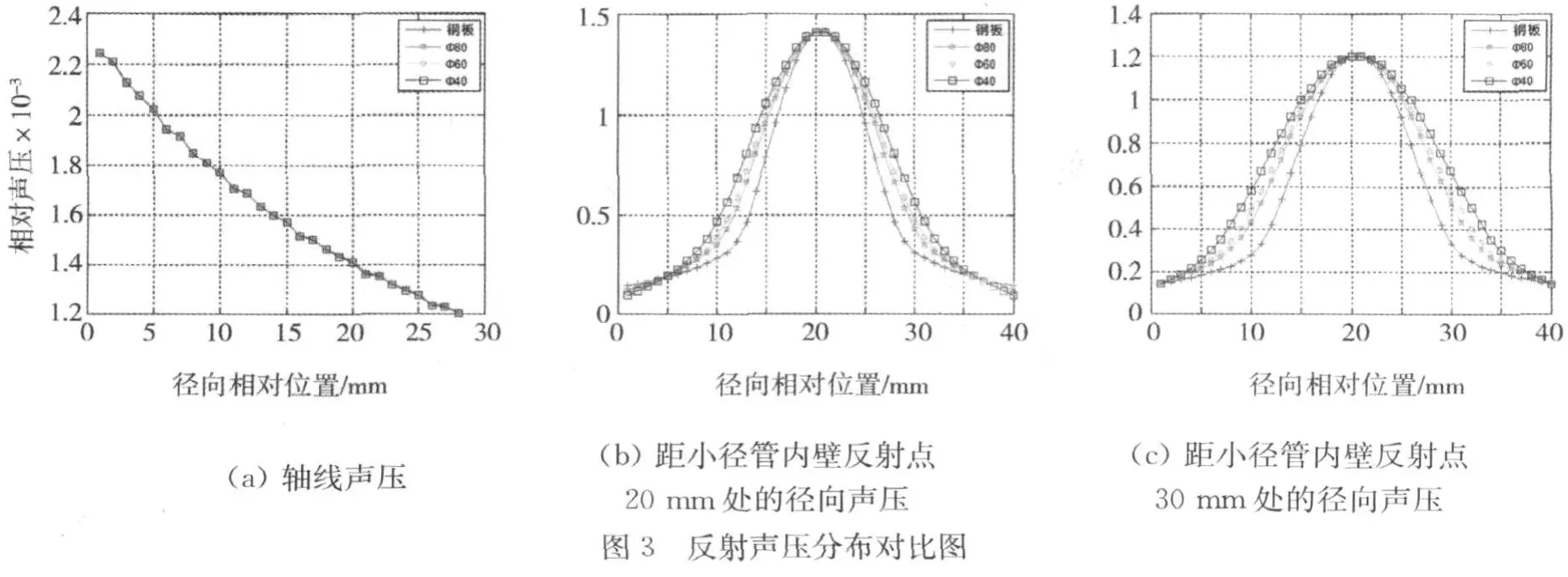
由互易原則可知：反射體上的聲壓分布決定了最終探頭接收到回波信號的大小,因此軸線附近小缺陷的回波信號受曲率影響較小,而大尺寸(尤其是長條狀)缺陷的回波信號受曲率影響較大。

2 不同規則反射體回波信號的對比分析

檢測的小徑管外徑為48 mm,內徑為20 mm;根據電力系統標準[6],選用斜探頭晶片尺寸為6 mm×6 mm,入射角為70°,中心頻率為5 MHz。小徑管中設置三種不同的規則反射體：長橫孔φ1 mm×10 mm,孔軸線垂直于管材軸線,孔的形狀有兩種：其一為直孔,如圖4(a)所示,其二為彎孔,孔軸線同心于管橫截面,如圖4(b)所示,陰影區為管材橫截面,空白區為孔的橫截面;短橫孔為 φ1 mm×5 mm;球孔為φ3 mm。儀器的掃描速度按水平調整;二次波檢測過程中以規則反射體最大回波信號與DAC曲線(DL-1試塊各孔回波,相當于一次波檢測)作對比。

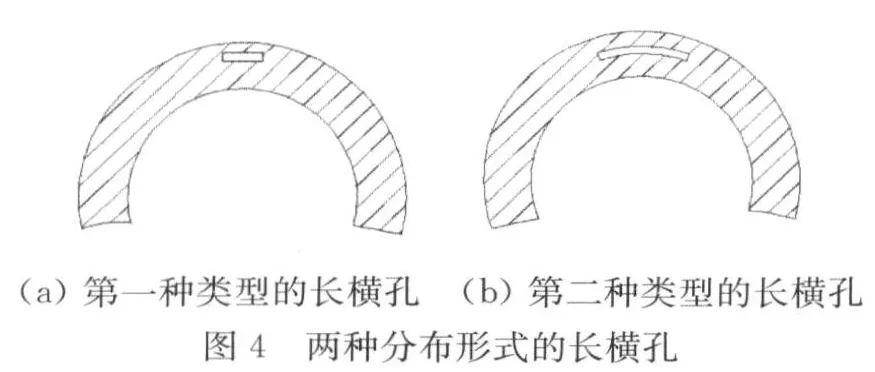
2.1 長橫孔的回波信號

假設小徑管中分別埋藏了7個與管道軸線垂直的第一種類型的長橫孔(φ1 mm×10 mm),孔中心點距探測面為1～13 mm,間隔為2 mm,利用UTCAS計算模型,計算二次波檢測時的各孔最大回波聲壓,得到的計算結果如圖5(b)所示,圖中的DAC曲線由一次波檢測DL-1試塊中標準孔的最大回波信號繪制所得。由此可知,在相同聲程條件下,長橫孔的二次回波聲壓小于DL-1試塊中孔的回波聲壓(即一次回波聲壓),且差值隨探頭至缺陷距離的減小而增大,最大差值達5.2 dB。這一現象恰好驗證了圖3(b)與(c)所給出的計算結果。

另假設小徑管中分別埋藏了7個與管道軸線垂直的第二種類型的長橫孔(φ1 mm×10 mm),孔的位置與第一種相同,圖5(b)的計算結果顯示出：在相同聲程條件下,第二種長橫孔的二次回波聲壓大于第一種長橫孔的二次回波聲壓,其中最大差值達7 dB;這是長橫孔的彎曲對聲束聚焦產生的影響。

2.2 短橫孔的回波信號

假設小徑管中分別埋藏了7個與管道軸線相互垂直的短橫孔(φ1 mm×5 mm),孔的埋藏位置與長橫孔相同,對其進行二次波檢測;為了與一次波檢測進行對比,又假設在圖6(a)試塊中埋藏相同的短橫孔,探測面的曲率半徑為24 mm,孔中心距離檢測面15～27 mm,間距2 mm。利用UT-CAS計算模型個計算短橫孔的最大回波聲壓,計算結果如圖6(b)所示：同深度的短橫孔一次回波與二次回波聲壓相近,最大差值也僅為1.9 dB,這是聲束軸線附近反射體的回波信號受管內壁曲率影響較小導致的;在相同聲程條件下,短橫孔的二次回波聲壓小于DL-1試塊中孔的回波聲壓,且差值隨探頭至缺陷距離的增大而增大,其中最大差值達4.2 dB。

2.3 球孔的回波信號

假設小徑管中分別埋藏5個φ3 mm的球孔,孔中心點距探測面為3～11 mm,間隔2 mm,對其進行二次波檢測;為與一次波檢測對比,與圖6(a)的試塊尺寸相同,球孔中心距離檢測面17～25 mm,間距2 mm,利用UT-CAS計算模型計算球孔的最大回波聲壓,計算結果如圖7所示：同深度球孔的一次回波與二次回波聲壓相近,最大差值僅為0.1 dB,這同樣是聲束軸線附近反射體的回波信號受管內壁曲率影響較小導致的;在相同聲程條件下,球孔一次回波聲壓小于DL-1試塊中橫孔回波聲壓,且差值隨探頭至缺陷距離的增大而增大,最大值達3.3 dB。

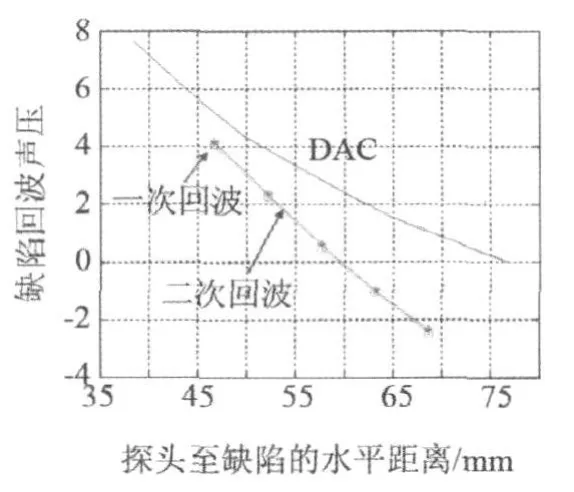
圖7 球孔回波聲壓與DAC曲線的對比

從以上仿真計算的結果及對比,結合實際小徑管焊縫二次波檢測,可以知道：

(1)小徑管內壁曲率對點狀缺陷影響小,而對條狀缺陷影響大。

(2)小徑管內壁曲率對焊縫根部條狀缺陷的影響較大,而對焊縫表面的條狀缺陷的影響較小。

(3)小徑管內壁曲率對焊縫根部點狀缺的陷影響較小,而對焊縫表面的點狀缺陷的影響較大。

3 結語

將UT-CAS聲場計算模型應用于小徑管焊縫二次波檢測。計算結果發現,小徑管內壁曲率對不同形狀和埋藏深度的缺陷檢測結果均存在影響,其中點狀缺陷的影響較小,條狀缺陷的影響較大,其中兩種長條狀缺陷的回波聲壓差值最大達7 dB,因此實際小徑管焊縫的二次波檢測必須考慮管材曲率對回波信號的影響。

[1]Calmon P.Recent development in NDT simulation[C].WCU2003,Paris,2003：443-446.

[2]Wirdelius H.The application of mathematical modeling of ultrasonic NDT in the qualification process[J].ECNDT,1998,13(11)：1-4.

[3]Michael Garton.Refining automated ultrasonic inspections with simulation models[EB/OL].1997-10/2007-06-08.http：//www.ndt.net/article/garton/garton.htm.

[4]丁輝,張俊,等.超聲檢測聲場計算模型的建立與仿真軟件的開發應用[J].無損檢測,2009,31(8)：614-618.

[5]Lhemery A.Impulse response method to predict echo responses from defects in solids,Part1,Theory[J].J.Acoust.Soc,Am,1995,98(4)：2197-2208.

[6]DLT 820—2002 管道焊接接頭超聲波檢驗技術規程[S].