基于殘差修正的GM(1,1)模型的我國人均糧食產量預測

楊 陽

（西南政法大學，重慶401120）

0 引言

經濟預測指通過對歷史數據、現象的總結歸納，發現內在波動規律并構建相關框架和方法，對未來的經濟走勢進行期望假設的過程。目前預測的方法很多，定性和定量作為預測的兩大工具，越來越呈現出互相補充、互為檢驗的良性關系。定性預測的頭腦風暴法、德爾菲法曾經和正在被廣泛使用，但定量預測的運用正在被全面推廣，如線性計量方程、馬爾科夫鏈、空間狀態方程、灰色理論等，各種預測工具各有優劣，甚至相關學者提出使用變權重組合模型對眾多預測方法進行整合，以縮小預測誤差而提高精度。筆者認為，首先數量經濟預測方法（如計量回歸）需要大量的數據，那么由于統計資料的缺失或誤差導致模型整體效度不高、模型不可能窮盡所有影響因素而引起隨機擾動項不真實；馬爾科夫鏈強調無后效性，即當期數據包含了以往歷史數據所有信息，下一期現象只與本期數據和轉移概率有關，需要強有效市場理論的支持，這些在現實當中是不成立的，所以一切計量預測方法都具備了一些與現實不相符合的假設，必然導致誤差。其次變系數組合預測法固然能夠取不同預測模型之長以提高精度，但預測模型多種多樣，在紛繁復雜的經濟現象下不可能將所有的預測方法都使用一次后再進行變系數組合，這樣做不僅復雜而且所得出的系數也僅僅是在一小段時間內有效。綜上所述，灰色系統能夠相對于其他預測模型更能從本質上揭示數據運動規律，并且所需要的樣本區間較其他方法少，將由隨機擾動項引起的沖擊序列進行灰——白轉變。但任何模型都存在著預測誤差問題，誤差反映在模型中為隨機擾動項，故本文對GM(1,1)預測模型的尾端殘差序列進行白熱化方程進行時間相應函數求解，以期消除誤差，并通過實際案例進行分析以體現其在經濟預測中的價值。

1 殘差修正的GM(1,1)模型

目前關于灰色預測方面的理論研究非常多，本文無意于去討論已經成熟的模型形式，而著重探討模型中的經濟含義和變量作用。GM(1,1)模型表示一階條件下單變量的灰色預測模型，有基本形式和原始形式之分。

原始形式是指 x0(k)+ax1(k)=b，其中 x0(k)為原始序列，x1(k)為一次累加序列，那么由簡單OLS可求出a,b兩個參數，具體意義是a為發展系數，及累加序列每變動一個單位給原始序列帶來的影響作用大小，成為發展系數。假設x0(k)是一個成倍數增長的簡單序列，如x0(k)=Ck，C為常數，那么很容易求出a與b之間存在的簡單線性關系。基本形式是計算出x1(k)的緊鄰均值序列z1(k)，然后將其替代x1(k)，形成x0(k)+az1(k)=b，替代的目的在于使用累加序列緊鄰均值可比較好的控制趨勢放大效應，即緩沖算子作用。求得參數a,b的回歸矩陣可表示為

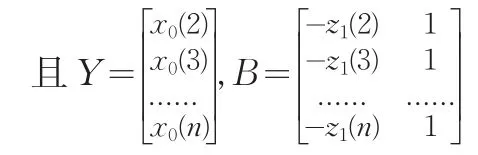
則GM(1,1)模型x0(k)+az1(k)=b的最小二乘估計參數列滿足x0(k)+az1(k)=b的時間響應函數序列為

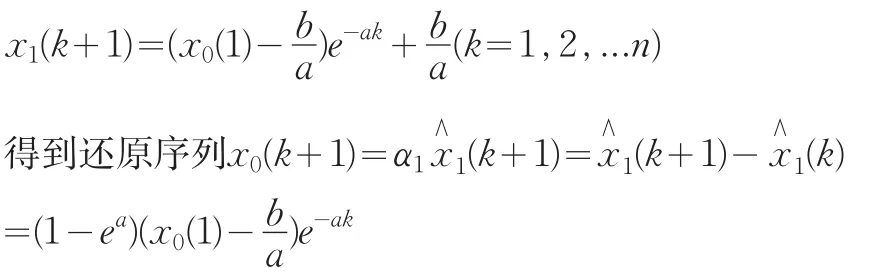
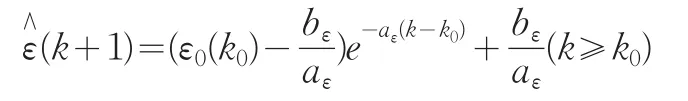
從K0開始的ε0的預測序列為

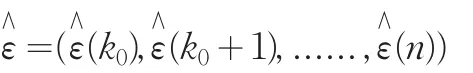
其中，

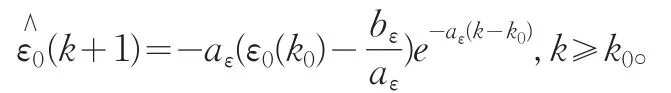
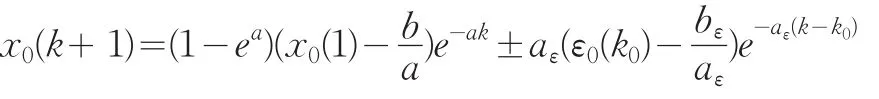
殘差修正的GM(1,1)基本理念是：既然原始觀測序列存在內部規律可用灰色處理得到提取值那么預測與觀測序列所形成的誤差必然有一部分屬于系統真實序列，同樣可以采取時間相應公式處理，克服了以往計量方法無法再從殘差即隨機擾動項中提取有價值信息的不足。值得說明的是上述提高的K0是截取誤差項的起點值，這并不意味著必須要從長度為n的殘差序列中后半段開始提取，可以通過比較不同時點上預測誤差的大小，進行有針對性的選取，在本文下面的例證中就使K0為2，即全范圍的提取，從整體預測角度去減少誤差。當然在相關研究中作者們可以根據實際情況選取K0。

2 實證分析

2.1 我國糧食產量的統計分析

根據以上的灰色模型及殘差修正分析，選取2000～2009年的我國人均糧食產量為研究對象，數據來源于《中國統計年鑒》（2009）。進行GM(1,1)預測，并通過對尾端殘差的1—AGO序列建立時間相應函數求解，對預測模型進行更正。我國作為傳統意義上的農業大國，在向工業化強國邁進的道路上一直沒有忽視糧食安全的重要性，但自1998年糧食產量達到歷史頂峰后，由于耕地面積減少、農村勞動力大量外流和技術基礎過低等綜合因素2003年糧食不增反減，曾經一度引起恐慌。但中央采取了一系列的“三農”扶持政策，加大了對農業的政策傾斜力度與投資，克服了干旱等自然災害，實現了七連增的大豐收。但也應清楚的認識到雖然糧食總量連年增加，但增加的幅度很小，以2000年為基數2009年的增加幅度為14.85%，年平均增長率不到1.5%，不僅小于國家在農業投資上的增速也小于農民收入增速，體現了糧食增產工作是系統工程，需要各項支持協同努力才能夠發揮顯著效果，目前的糧食政策有待改善。人口眾多是我國的一大基本國情，人口的增長在短期內并不意味著勞動力的增多，所以經濟不會以新古典經濟增長模型中的勞動力添加模式發展，實際上降低了人均占有資源，有學者經過統計改革開放24年以來人均糧食產量劃了一個圈-回到了原點。上述觀點可從表1看出。人均糧食產量由總產量和國民人數決定，過低一方面體現了糧食產量增速緩慢，另一方面也反映了計劃生育在我國的執行力度不夠，沒有達到相應的目標。

2.2 糧食產量GM(1,1)預測

灰色預測是使歷史數據序列由灰轉白的過程。根據第一節的理論敘述，經過以下流程對人均糧食產量進行預測：

表1 我國糧食總產量及人均產量

（1）累加生成序列1-AGO的生成

根據系統觀測行為序列

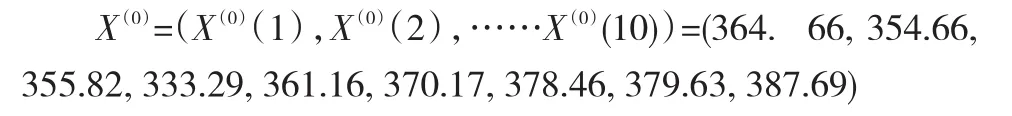
得到1-AGO序列：

運用數據序列進行灰色系統建模的前提是序列X（0）為非負準光滑序列，而X（1）具有準指數規律，下面進行驗證。首先進行X（0）光滑比P（k）值計算，結果如表2。表2中2001年的P（k）值為0.972，其他年費均小于0.5，而P（k+1）/P（k）在八個時點上均通過檢驗，故認為考察時間段內非負準光滑序列驗證通過；同理，得到前后年數據之比O（k），數據同見表1，浮動區間為[0.9367,1.0836]，極值＜0.5,可知數據序列存在準灰數指數規律。

（2）緊鄰均值Z(1)生成及預測模型估計

上文已經通過了灰色建模的前提條件檢驗，生成緊鄰均值序列

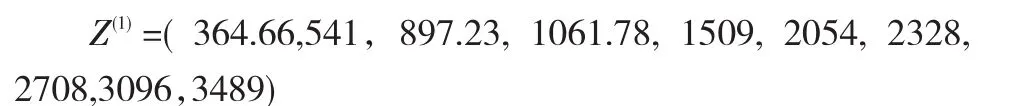
由于白熱化方程的形式為X(t)+aZ(t)=b，通過最小二乘法進行估計的矩陣形式是

表2 非負準光滑序列及準指數規律驗證

得到發展系數為0.0149，絕對值小于2說明GM模型穩定，并且根據[-2/(n+1),2/(n+1)]原則，有較高精度。則可得到相應的時間函數式22880.504304，經過DPS軟件測算后得到擬合序列，見表3。

表3的第三列為預測誤差，第四列為相對誤差，發現擬合效果不好，殘差平方和C為0.7046，平均相對誤差P=0.5556。對未來5期進行預測得到 X(t+k)=399.16069，405.15455，411.23841，417.41363，423.68157。

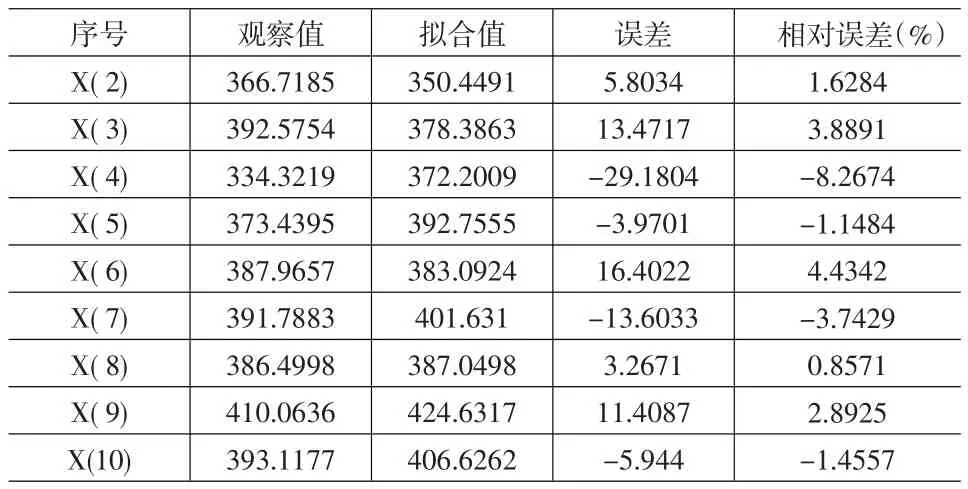
表3 DPS處理的GM(1,1)預測結果

3 殘差序列修正的模型

根據上述討論目前所得到的結果并不良好，根據誤差序列均取絕對值，得到

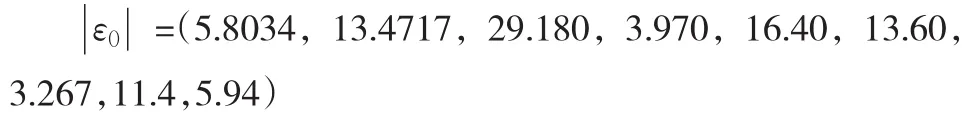
建立GM（1，1）模型，得 ε0的1-AGO序列 ε1的時間響應式

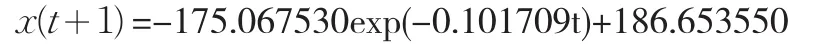
其中，a=0.101709，b=18.984327。其導數還原值為

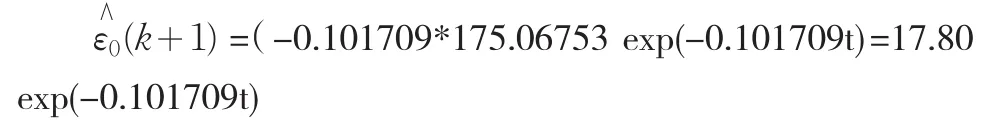
得到殘差修正后的預測模型為

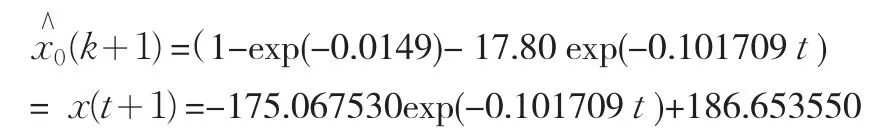
預測的模型擬合值、殘差序列、相對平均誤差見表4。殘差平方和提升到0.8889，模型評價結果為好。對未來5年的預測結果為：394.35298，399.69133，405.18307，410.82343，416.60824公斤/人。從這里反映了兩個問題：一是由于糧食產量為明顯上揚序列，進行模擬預測時殘差的擴大是由于趨勢的放大效應一起的，殘差修正后的預測模型比未修正條件下的更具有收斂性，從預測結果對比可看出，修正結果較以前波動小。

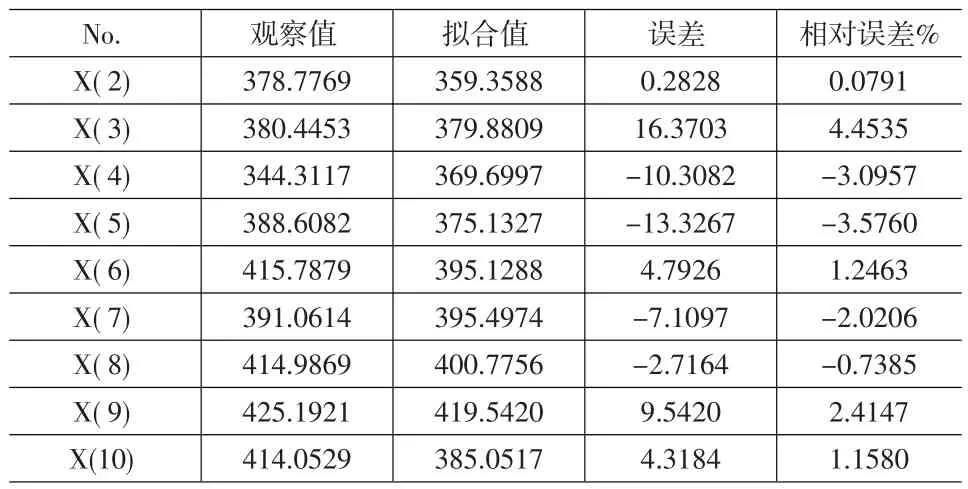
表4 殘差修正后的GM(1,1)預測結果

灰色理論認為當兩個波動序列形狀和趨勢越接近，則兩者之間存在灰色關聯關系，這里通過實際序列和兩個預測序列之間的關系圖（圖1）可以看出，修正后的預測序列更與實際序列接近，而與傳統預測方法存在的根本差異在于：灰色理論認為行為序列（即實際值）并不是真實序列，而灰色處理的任務就是從行為序列中提取真實序列并消除擾動項，但其他方法卻與此相反，大多方法以觀測序列為實際序列。

3 結論

經過基于殘差修正的GM(1,1)預測模型相關討論和實證，得到以下結論。

(1)灰色模型無論是在理論基礎還是實踐運用中均較其他計量模型更為實用和簡便，且不失邏輯基礎。現實經濟社會活動紛繁復雜，建立模型時不能包含全部因素，并且由于統計手段的局限性數據缺漏是常見現象。王明禮認為灰色模型是指利用離散隨機數經過生成變為隨機性被顯著削弱而且較有規律的生成數，建立起的微分方程形式的模型，是一個將信息由灰變白的過程。緩沖算子的提出使得原始數據的處理更具規律性、可控性和系統性，能夠根據實際經濟現象和發展趨勢對原始數據進行調整，擯棄了以往觀測數據等于真實數據的誤區。

(2)灰色系統殘差修正克服了其他計量模型不能對隨機擾動項進行再次提取有效信息的缺陷，更重要的是從殘差序列本身入手，不會帶來如回歸方法中增減自變量帶來的偽回歸和異方差，并且這種殘差修正過程可以多次進行，直到殘差信息被很好提取為止。本文實證中的結論證明了殘差修正使預測精度大大提高，通過了相關檢驗。并且緩沖算子的存在也使灰色算法與其他算法結合得以實現，如姚作芳等使用markov法對灰色預測結果進行修正；張大斌(2009)提出了一種基于遺傳算法調整發展系數和內生灰作用量的灰色預測模型,將遺傳算法系數作為灰色緩沖算子。

（3）我國糧食產量預測情況說明，未來5年我國人均糧食產量增速要小于以前，年增量為5～6公斤/人，小于2003～2009期間的8～10公斤/人。當然，預測的結果是基于目前發展態勢的前提，如果產業政策和科技水平有了很好的調整，情況會發生相應變化，特別是黨的十七大上提出的確保糧食安全、建設產量基地等大力發展糧食產業的措施，這些都會造成系統行為規律的變動。糧食產業包含很多子行業，如水稻、玉米和小麥行業，需要尋找對糧食產業貢獻最大的子產業，進行區別財政支持。目前有學者對糧食產業結構進行分析，賴紅兵通過建立糧食產量的誤差修正模型,發現水稻波動對糧食產量波動的影響顯著,其次是玉米和小麥。對提高糧食產量這項國家任務需要進行定量分析，以確保糧食產業穩步發展。

圖1 預測效果對比圖

[1]鄧聚龍.灰色系統基本方法[M].武漢:華中理工大學出版社,1987.

[2]王明禮.三種灰色系統模型的預測比較[J].統計與決策，2011,（8）

[3]姚作芳,劉興土,楊飛.馬爾科夫方法修正的灰色模型在吉林省糧食產量預測中的應用[J].地理科學，2010,（3）.

[4]張大斌,朱侯,李威,張景廣.一種基于遺傳算法的灰色模型在鐵路客運量預測中的應用[J].統計與決策，2009,（24）.

[5]賴紅兵.中國糧食產量波動及其結構分析[J].農業技術經濟，2009,（5）.