直線永磁無刷直流電動機端部力的分析

黃文美，薛雅潔，宋桂英

(河北工業大學，天津300130)

將式(4)和式(5)代入式(3)中，簡化后得:

0 引 言

直線永磁無刷直流電動機具有推力大、定位精度高及易于控制等優點，越來越多的應用于工業自動化，有著廣泛的應用前景。直線電動機是一種將電能直接轉換成直線運動機械能而不需要任何中間轉換機構的裝置;傳統的有刷電動機中電刷和換向器組成的機械換向裝置，其間的滑動接觸嚴重的影響了電機的精度和可靠性，縮短電機壽命，需要經常維護，所產生的火花會引起無線電干擾。無刷直流電動機采用功率電子開關(如GTR、MOSFET、IGBT)和位置傳感器代替電刷和換向器組成機械換向器，既保留了直流電動機優良的運行性能，又具有交流電動機結構簡單、維護方便和運行可靠等特點［1－2］。

直線永磁電機也有其不足之處。與旋轉電機相比，直線電動機最大的不同之處在于它的動子鐵心是長直的、開斷的，所以，動子鐵心端部磁場會發生畸變，這就影響到行波磁場的完整性，進而對電機推力造成波動影響，影響電機的性能，這就是端部效應。而直線電動機的特殊結構使得端部效應是不可避免的，在實際應用中應設法削弱端部力，使電機系統的失穩性降低。文獻［3］采用斜極法來削弱端部力，這種方法不易于電機加工，實際應用意義不大;文獻［4］中采用遺傳模擬退火算法削弱推力波動，得到了合理的電機參數，但是這種方法對于電機結構參數具有約束性，只是針對部分型號電機，不具有普遍性;文獻［5］采用線圈補償的方法來削弱端部力，這會增加電機的重量和成本，也不利于電機控制。

本文提出了從優化動子結構方面來削弱端部力的方法，并建立了仿真模型，驗證了該優化方法的可行性。這種方法易操作，成本低，適合大部分直線電動機。

1 直線永磁無刷直流電動機動子長度的優化

1.1 端部力數學解析模型

直線永磁無刷直流電動機模型的磁場分布如圖1所示，動子模型忽略了齒槽結構。可以看出動子鐵心兩端端部磁場發生畸變，當給線圈繞組通入三相正弦交流電時，動子鐵心在這個磁場作用下做直線運動，但是由于直線電動機鐵心端部發生開斷，使得兩個端部的線圈電感和動子鐵心中部的線圈電感不同，造成三相繞組的磁通不等，端部磁導和永磁體作用形成了兩個切向的推力F1、F2，這兩個力之和即為永磁直線無刷直流電動機的端部力Fend:

各力的分布示意圖如圖2所示。

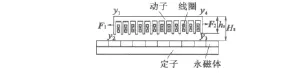
圖2 永磁直線無刷直流電動機模型

根據麥克斯韋張量法，推算出電機水平推力表達式:

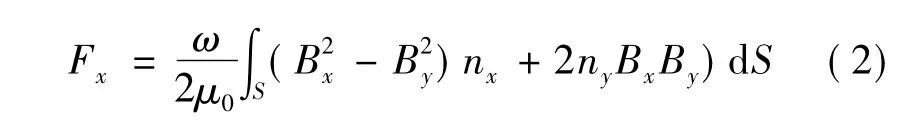
式中:μ0為磁導率;ω 為動子縱向厚度，Bx、By分別為電機磁場水平和垂直方向分量。S為包圍動子鐵心的曲線，nx、ny為法向量分量。

由式(2)可計算出式(1)的端部力。可得:

根據氣隙磁場的推導，得:

式中:Br為永磁體的剩磁;τ為極距;τs為永磁體寬度;hs為動子鐵心的高度;Hs為動子鐵心到永磁體表面的高度。令:

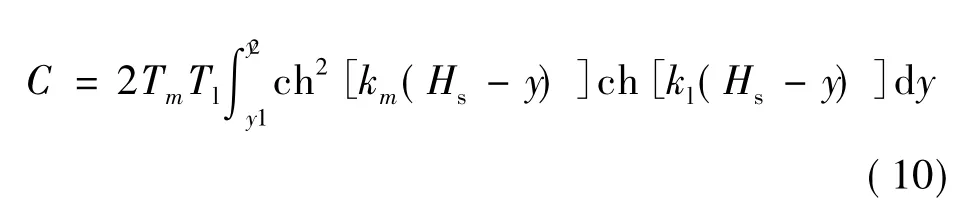
將式(4)和式(5)代入式(3)中，簡化后得:

式中:x0為動子鐵心中心位移坐標;L為鐵心長度。

從式(11)中分解出各項系數，分別為:1+

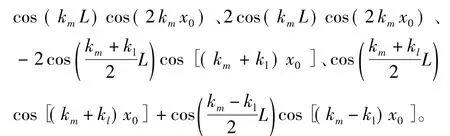
從以上各項系數中可以看出，當L一定時，這些系數都是關于x0的周期函數，且周期為極距τ;當動子在0～τ范圍運動時，這些系數是隨著L周期性變化，且周期為 2τ;當 L=(0.5+n)τ，n=1，2，3，…時，cos(kmL)等于零。

通過以上分析可以得出，端部力的波動是和動子位置相關的周期性波動函數，且周期為極距τ;當動子在0～τ內運動時，端部力的大小和動子長度有關，周期為2τ，若僅考慮幅值變化，則周期為τ;當L=(0.5+n)τ，n=1，2，3，…時，端部力有最小值。

1.2 有限元法實驗驗證

永磁直線無刷直流電動機參數如表1所示。

表1 電機仿真模型參數

建立如圖1所示的忽略齒槽結構的Ansoft仿真模型，以動子長度L為變量，利用有限元法進行驗證，結果如下:

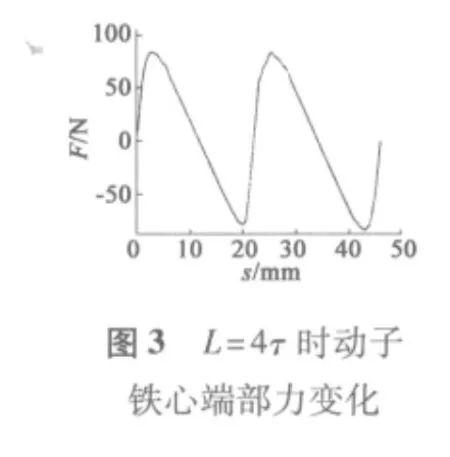
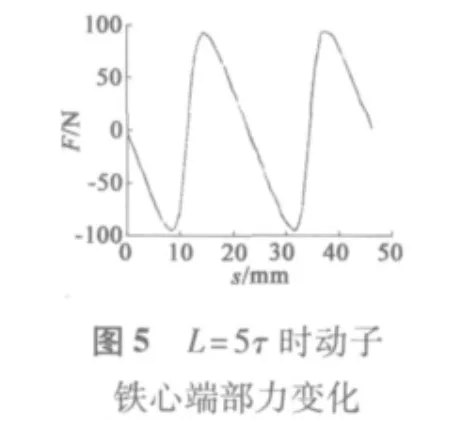
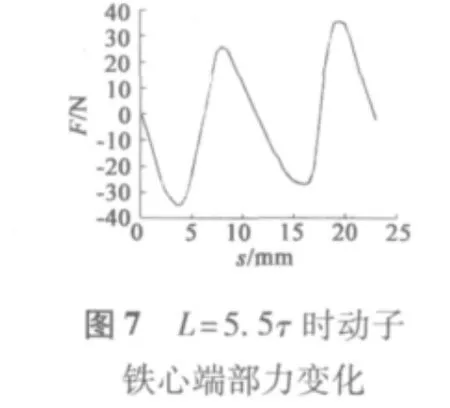
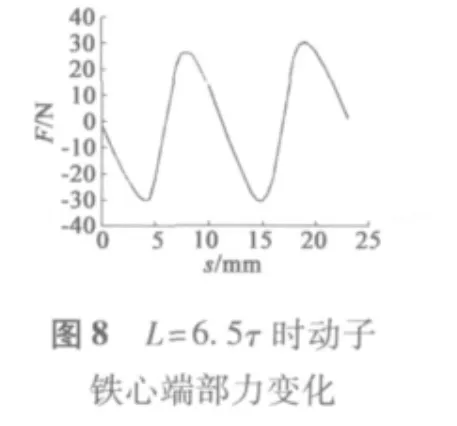
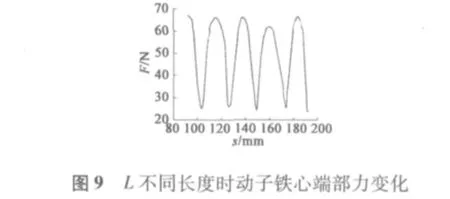
1.3 實驗結論分析

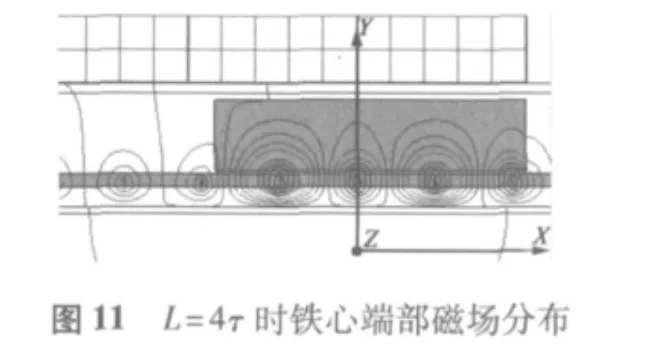
通過對比不同動子長度下的端部力大小，從圖3～圖6中可以看出，當動子長度在0～2τ范圍內運動時，端部力大小呈周期性變化，且周期為τ;端部力變化在L=4τ和L=6τ時基本相同，最大值約為89 N，與L=5τ時幅值基本相同，相位相差180°;當L=7.5τ時相較于L=4τ、L=5τ時端部力波動范圍較小，最大值約為40 N;從圖9中可以看出，端部力是隨著鐵心長度周期性變化的，且在L=(k+0.5)τ時端部力有最小值。圖10、圖11中顯示出L=7.5τ和L=4τ時磁場分布，可以看出，在忽略齒槽結構模型中鐵心端部磁場分布在L=7.5τ時優于L=4τ時動子鐵心端部磁場分布。圖6～圖8對比了L=5.5τ、L=6.5τ、L=7.5τ時端部力的變化，可以看出L=6.5τ時端部力最大值較小，約為30.7 N。

2 永磁直線無刷直流電動機動子形狀的優化

2.1 建立優化模型

由于端部效應是在鐵心端部的氣隙磁阻發生了急劇變化而導致的，因此可以把動子端部設計為過渡結構來削弱端部力。

2.1.1 圓弧過渡結構

圖12為鐵心端部為圓弧的較平滑結構的Ansoft仿真模型。

圖12 L=7.5τ時圓弧結構的鐵心端部磁場分布

2.1.2 梯形過渡結構

圖13為鐵心端部為梯形結構的Ansoft仿真模型。

圖13 L=7.5τ時梯形結構的鐵心端部磁場分布

2.2 實驗結論分析

圖14、圖15分別給出了鐵心端部采用圓弧過渡結構和梯形結構，當動子鐵心在0～τ范圍運動時端部力的變化。

可以看出，相較于圖6，采用圓弧過渡結構的動子鐵心端部力較小，其最大值由40.026 N下降到14.147 N，下降了約64%;而采用梯形過渡結構的動子鐵心端部力最大值約為53.8 N，相較于圖6則較大，所以實驗排除了梯形過渡結構的動子結構，選用圓弧過渡結構的動子結構。

3 結 語

本文針對永磁無刷直流電動機的端部效應問題，結合對端部力的理論分析以及運用有限元法仿真，通過對不同動子長度時端部力的比較，證明了通過改變動子長度來削弱端部力是可行的;端部力是關于動子長度的周期函數，當動子長度為(k+0.5)τ時，端部力有最小值;其次，采用Ansoft軟件計算了動子端部圓弧結構和動子梯形結構時端部力的大小，驗證了動子端部采用圓弧結構時端部力相對減弱。這在實際應用中削弱端部力對推力的波動影響有很大幫助。實驗確定動子長度為149.5 cm，端部為圓弧過渡結構，有限元法計算端部力最大值約為8.7 N。

［1］ 夏加寬.高精度永磁直線電機端部效應推力波動及補償策略研究［D］.沈陽:沈陽工業大學，2006.

［2］ 李皞東.電火花機床用永磁直線電機的端部效應及其控制的研究［D］.沈陽:沈陽工業大學，2002.

［3］ Lee S－H，Park S－B，Kwon S－O.Characteristic analysis of the slotless axial－flux type brushless DC motors using image method［J］.IEEE Transactions on Magnetics，2006，42(4):1327 －1330.

［4］ 陳宇，盧琴芬，葉云岳.長定子同步直線電動機的設計及其優化［J］.電工技術學報，2003，18(2):18 －21，40.

［5］ 李治源，關曉存.感應線圈炮電樞與驅動線圈間縱向動態邊端效應的影響［J］.微電機，2010(6):13－15.

［6］ 張穎.永磁同步直線電機磁阻力分析及控制策略研究［D］.武漢:華中科技大學，2008.

［7］ Lee J Y，Kim S I，Hong J P.Optimal Design of Superconducting Motor to Improve Power Density Using 3D EMCN and Response Surface Methodology［J］.IEEE Transactions on Applied Superconductivity，2006，16(2):1819 －1822.

［8］ Faiz J，Jafari H.Accurate Modeling of single－ sided linear induction motor considers end effect and equivalent thickness［J］.IEEE Trans.on Magnetics，2000，36(5):3785 －3790.