異步電動機的SVM－DTC控制

蔣建虎，姬宣德

(洛陽理工學院，河南洛陽471023)

0 引 言

直接轉矩控制是異步電動機高性能的控制方法。文獻［1］提出基本直接轉矩控制(BASICDTC)的方案，但轉矩脈動與磁鏈脈動一直制約著直接轉矩控制系統的性能。文獻［2］采用精細開關選擇表減輕了轉矩脈動和磁鏈脈動，但沒有從根本上解決問題。本文采用空間電壓矢量調制與直接轉矩控制相結合(SVM-DTC)的方法，以減小轉矩和磁鏈脈動，利用全階磁鏈觀測器觀測定子磁鏈以提高觀測精度，并提出一種單自由度極點配置方法實現磁鏈觀測器的極點配置。仿真結果表明，系統不但實現了轉矩和磁鏈的定量控制，降低了轉矩脈動和磁鏈脈動，提高了定子磁鏈的觀測精度，而且同時使得逆變器開關周期恒定，更易于數字化實現。

1 SVM－DTC基本原理

基本直接轉矩控制的控制思想是:在保持定子磁鏈幅值恒定的情況下，一個控制周期內依據磁鏈和轉矩誤差的正或者負，通過查表的方式選擇八個定子電壓矢量中的一個來控制磁鏈和轉矩增加或者減小的趨勢。由于逆變器產生電壓空間矢量的有限個數使得轉矩和磁鏈不能同時得到最佳調節，基于這一控制策略的轉矩脈動和磁鏈脈動必然較大。直接轉矩控制對磁鏈和轉矩的控制是一種“定性”的方法。為使轉矩和磁鏈得到合理的調節控制，PWM逆變器就必須能夠產生任意需要的電壓空間矢量。與傳統直接轉矩控制不同，SVM-DTC對磁鏈和轉矩的控制是一種“定量”的方法，在空間矢量模式下，具有逆變器開關周期恒定、減小轉矩和磁鏈控制脈動的優點。SVM-DTC運用SVM生成變換器所需的參考電壓矢量，這個參考電壓矢量同時包含轉矩控制與磁鏈控制的信息。

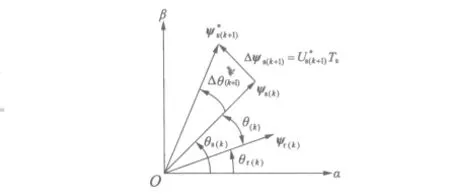
如圖1所示，磁鏈矢量在復平面上逆時針旋轉，θr為轉子磁鏈與橫軸α的夾角，θs為定子磁鏈與橫軸α的夾角，θ(k)為第k拍定子磁鏈與轉子磁鏈的夾角，即轉矩角，代表著第k拍轉矩的大小;ψs(k)為第k拍的定子磁鏈矢量為第k+1拍的控制目標定子磁鏈矢量，Δψs(k+1)為第k+1拍要求增加的定子磁鏈增量，這個增量由第k+1拍控制周期Ts的參考電壓矢量來完成。顯然的徑向分量代表了磁鏈控制的需求，的切向分量代表了轉矩控制的需求。因此，由圖可以得到第k+1拍參考電壓空間矢量的計算式:

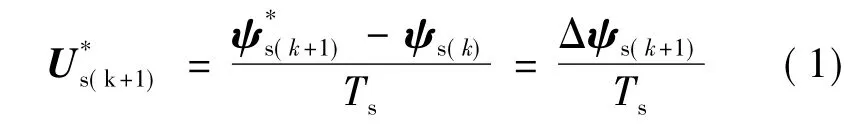
為精確起見，應考慮到定子電阻壓降，在兩相靜止坐標系中，參考電壓空間矢量:

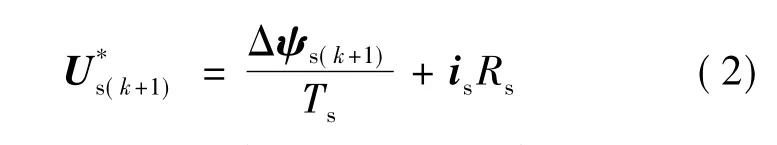
SVM-DTC利用轉矩和磁鏈的偏差通過兩個PI調節器，分別生成電壓空間矢量的切向分量和徑向分量，然后由SVM生成逆變器的開關信號，使得轉矩和磁鏈脈動大大減少。與基本直接轉矩控制不同，SVM-DTC不是用查表的方式來實現電壓空間矢量的選擇，而是根據切向分量和徑向分量的要求實時生成任意幅值和任意方向的矢量，克服了基本直接轉矩控制策略在一個控制周期中只發出有限幅值和有限方向的電壓空間矢量。異步電動機SVM-DTC控制系統框圖如圖2所示。

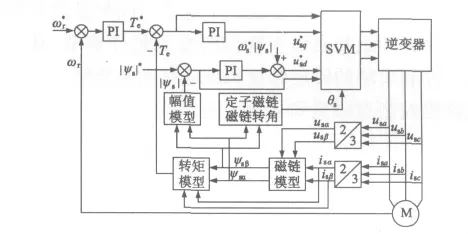
圖2 異步電動機SVM-DTC控制系統框圖

2 全階磁鏈觀測器

在兩相靜止參考系下，異步電動機可以用下列狀態方程描述:

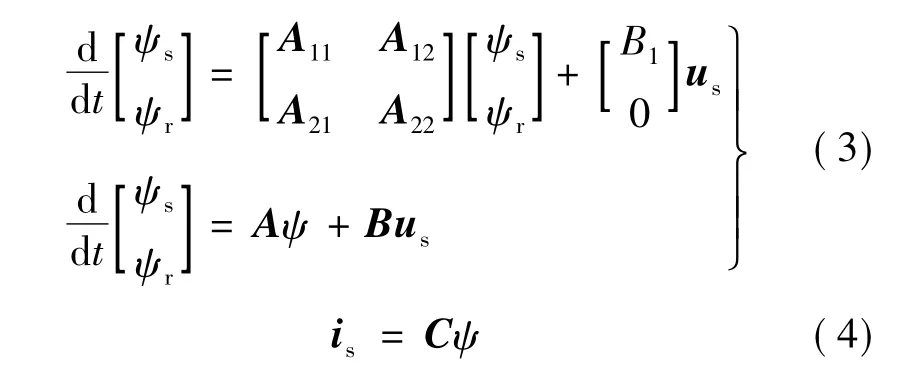
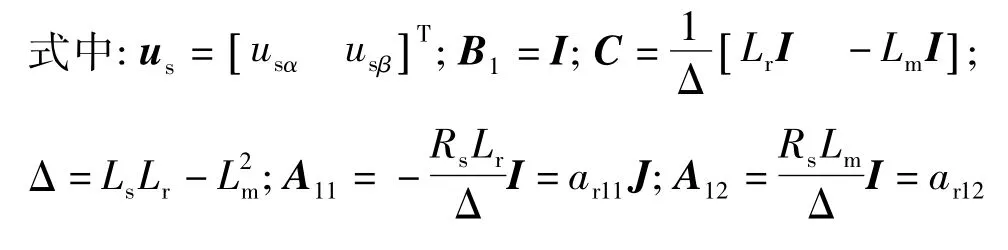
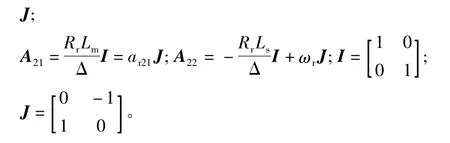
估計定子磁鏈和轉子磁鏈的狀態觀測器可以通過下列方程描述:

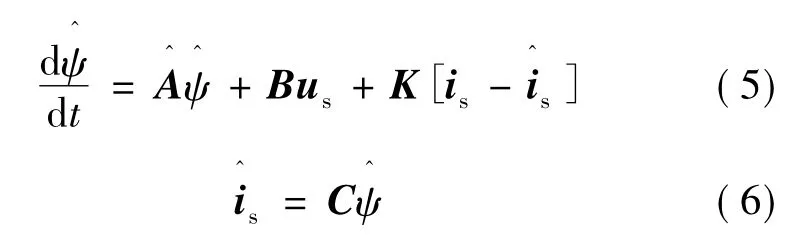
上述表達式中，“^”代表觀測器的估計值。K是觀測器增益矩陣。觀測增益矩陣K可以表示為如下矩陣形式［6］:

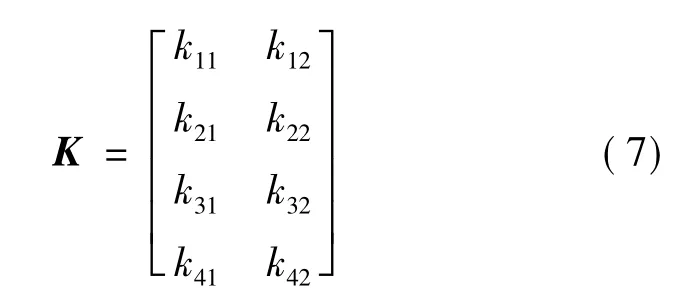
3 狀態觀測器極點配置方法

利用式(5)減去式(3)得到觀測器誤差方程:

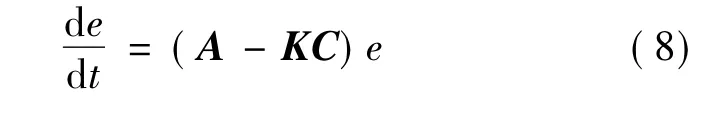
由式(8)可知，系統誤差e的收斂速度取決于系統矩陣A-KC的極點位置［7-8］。如果所選矩陣A-KC的特征值使得誤差向量的動態特性漸進穩定且足夠快，則任意誤差向量都將以足夠快的速度收斂于零(原點)。誤差向量e的收斂速度取決于系統矩陣A-KC的極點位置，通過增益矩陣K可以配置觀測器需要的任意極點位置。

式(7)的增益矩陣K有八個位置參數，極點配置極為復雜，文獻［9］把其參數縮減為四個，文獻［10］進一步縮減為兩個參數，增益矩陣K變為:

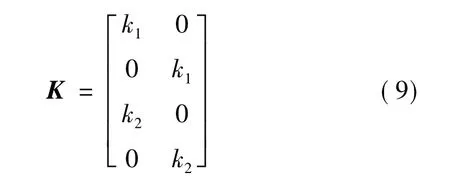
式(9)雖然解決了受電機參數和速度影響的限制，但是兩個參數的自由度還是使極點配置極為不方便。為了方便快捷有效地配置觀測器極點，本文提出一種新型配置方法，令式(9)中的參數絕對值相等，即:

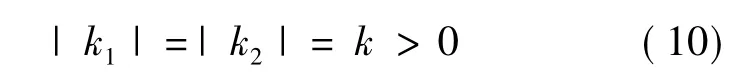
這樣參數只有四種可能:k1=k，k2=-k;k1=k，k2=k;k1=-k，k2=k;k1=-k，k2=-k。利用MATLAB繪出當k在0至1之間的十個數值(遞增量為0.1)時觀測器的極點軌跡，速度從零變化到基速，如圖3所示。

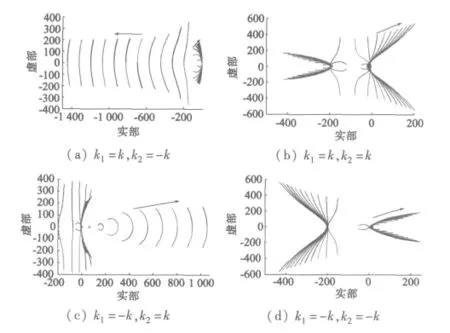
圖3 四種情況下觀測器極點的變化軌跡

由圖中極點變化軌跡可知，隨著k的增加，后三種情況中的一對極點實部變為正值，系統不穩定。增益矩陣K可以改變如下:

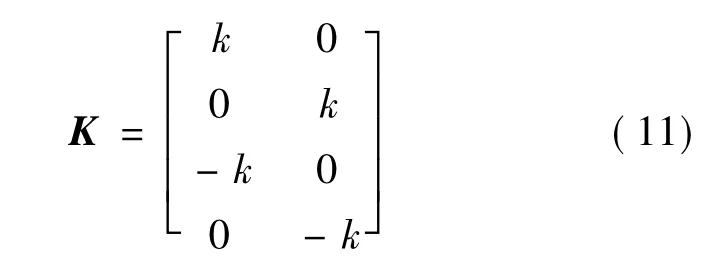
這樣，增益矩陣只有一個參數，在新型配置方法情況下，極點配置更為方便快捷有效。

從圖3可以看出，觀測器的極點是共軛復極點，其對應分量是衰減振蕩的。極點值的實部決定觀測器的快速性，虛部與實部之比決定觀測器的穩定性。從圖4可以看出，當k從1增加到11(增量為1)時，左一對極點的實部隨之增加，觀測器收斂速度加快，而穩定性變差。為了同時滿足觀測器快速性和穩定性的要求，觀測器極點實部的絕對值不能太大;右一對極點隨之接近虛軸，實部仍然為負，保證了觀測器穩定。

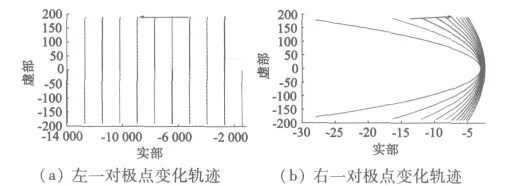
圖4 k為正整數時觀測器極點變化軌跡

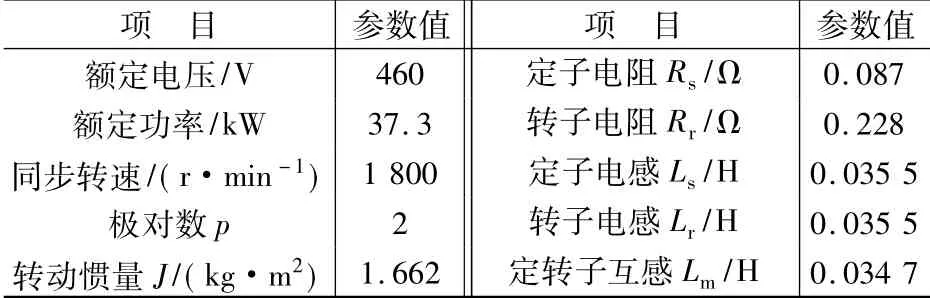
表1 異步電動機參數

4 仿真結果及分析

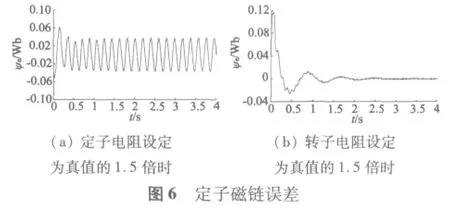
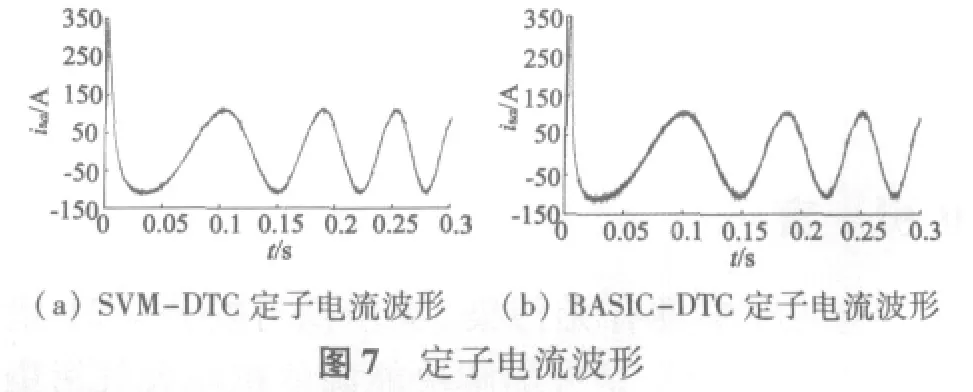
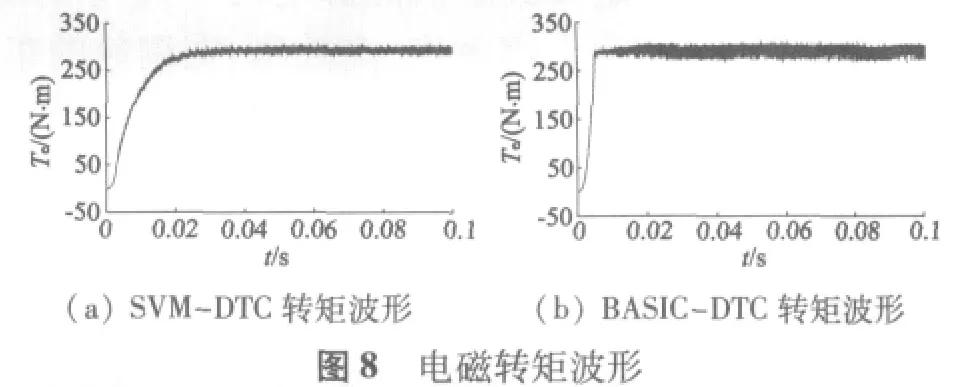
本文分別采用BASIC-DTC和SVM-DTC兩種方案對異步電動機系統進行仿真，并作出相應的比較，兩種方案均采用相同的電機參數，如表1所示。仿真結果如圖5～圖8所示。

從圖5(a)和圖6(a)可以看出，在定子電阻參數變化情況下，定子觀測磁鏈能夠快速跟蹤真實磁鏈，雖然幅值跟蹤有誤差(小于0.04)，但跟蹤相位相同，這一點對于直接轉矩控制系統尤為重要;從圖5(b)和圖6(b)可以看出，在轉子電阻參數變化情況下，觀測器也能實現磁鏈跟蹤，而且穩態跟蹤誤差幾乎為零，由此看出轉子電阻參數變化對定子磁鏈穩態值幾乎沒有影響;由此看出，在單自由度極點配置方法下，全階磁鏈觀測器對定、轉子參數變化具有很強的魯棒性。從圖7、圖8可以看出，與BASICDTC方案相比，SVM-DTC方案電流波形更接近正弦波，轉矩脈動減小，并使逆變器開關周期恒定，更易于數字化實現。

［1］ Depenbrock M.Direct self-control(DSC)of inverter-fed induction machine［J］.IEEE Trans.on Power Electronics，1988，3(4):420-429.

［2］ Casadei D，Serra G，Tani A.Implementation of adirect torque control algorithm for induction motors based on discrete space vector modulation［J］.IEEE Trans.on Industry Applications，2000，15(4):769-777.

［3］ Song Wen-xian，Yao Gan，Zhou Wen.Pole Arrangment Method of Full-OrderState Observer for Asynchronous Motor［J］.Motion Control and Apllication，2008，35(9):6-10.

［4］ Marchesoni M，Segarich P，Soressi E.A simple approach to flux and speed observation in induction motor drives.IEEE Trans.Industrial Electronics，1997，4(4):528-535.

［5］ Kojabadi H M，Chang L.Comparative study of pole placement method in adaptive flux observers［J］.Control Engineering Practice，2005，13(6):749-757.

［6］ 鄭澤東，李永東，王琛琛.異步電機全階自適應磁鏈觀測和速度辨識研究［J］.電氣傳動，2006，36(7):7-10.

［7］ 奚國華，高宏洋，許為.定子磁鏈全階觀測器增益矩陣的確定方法［J］.中南大學學報，2008，39(4):793-798.

［8］ 黃文新，李勇，胡育文.用空間電壓矢量調制異步電動機的直接轉矩控制［J］，南京航空航天大學學報，2007，39(1):127-132.

［9］ 郎寶華，劉衛國，周熙煒.基于參考磁鏈空間電壓矢量調制策略的PMSM-DTC系統［J］.電氣傳動，2007，37(7):21-25.

［10］ 張繼勇，李新兵，束長寶.基于空間矢量無速度傳感器感應電機的直接轉矩控制［J］.機械電子工程，2005，22(3):22-25.