超低速永磁同步電動機及其在坦克炮控系統中的應用

2011-11-20 08:35:02李立宇李長兵朱志昆

微特電機 2011年12期

李立宇，李長兵，朱志昆，袁東

(裝甲兵工程學院，北京100072)

0 引言

炮控系統是坦克火力控制主線末端的執行系統，具有驅動和穩定坦克火炮/炮塔的功能，是充分發揮火控系統性能，實現“先敵開火、首發命中”的重要保證［1］。不管是電液式還是全電式炮控系統，由于驅動電機的旋轉速度通常都很高，故系統中都需要由多級齒輪組成的減速機械傳動裝置。而齒輪傳動裝置中不可避免地存在傳動間隙及齒輪彈性形變，這一非線性環節對炮控系統的穩定性、低速性能和穩定精度(通常認為系統穩定精度僅能達到系統傳遞誤差的1/2左右)會產生重大影響，這就制約了系統性能的進一步提高。

本文提出的座圈電機無間隙傳動方案，水平向采用大直徑、多極、超低速永磁同步電動機，并設計成與現有炮塔座圈相似的結構，電機定子與車體聯接固定，電機轉子直接與炮塔固定，轉子轉動直接驅動炮塔旋轉。無間隙傳動方案消除了炮控系統中機械傳動間隙帶來的技術瓶頸問題，為炮控系統性能的進一步提升，探索了一種新的技術解決方案。

1 電機參數選型

根據某型坦克座圈結構，可確定座圈電機的定子外徑和轉子內徑尺寸;根據該坦克炮控系統最大調炮速度和最低瞄準速度等性能指標及斜坡調炮要求，可折算出電機轉速為0.003～5.83 r/min，額定功率為1.8 kW，額定轉矩為2 950 N·m。根據上述基本參數要求，考慮到推力軸承的最大游隙量，經計算和仿真分析，方案設計中所確定的電機參數如表1所示。

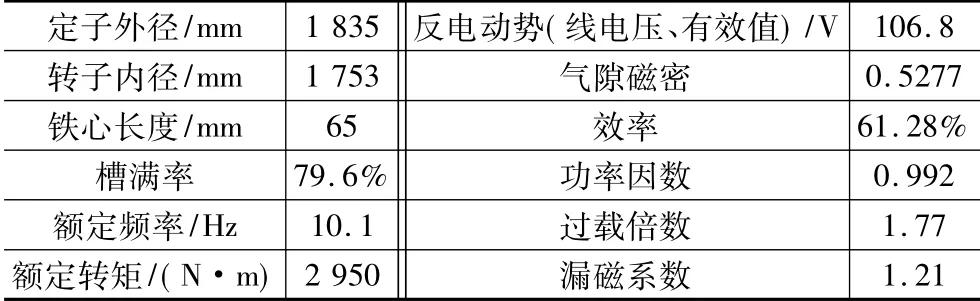
表1 電機性能參數

2 電機電磁設計

2.1 極槽配合的選取

不同的極槽配合對電機轉矩波動的影響也不同［2］。本文對208極234槽和198極216槽兩種極槽配合的永磁同步電動機進行對比分析后選取較優的極槽配合方案。

用Ansoft軟件對兩臺電機進行建模，分析其一個單元電機的空載氣隙磁場波形如圖1和圖2所示。

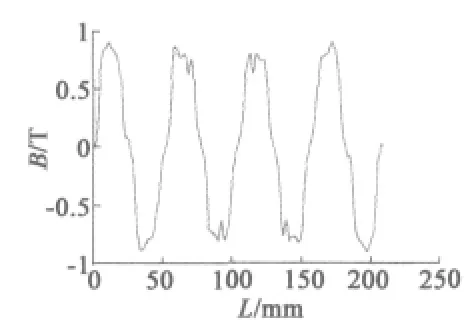
圖1 208極234槽永磁電動機氣隙磁密波形

圖2 198極216槽永磁電動機氣隙磁密波形

用傅里葉分析軟件對以上兩臺電機的氣隙磁密波形進行諧波分析所得諧波幅值占基波幅值的百分比，如圖3和圖4所示。

圖3 208極234槽永磁電動機氣隙磁密分析

圖4 198極216槽永磁電動機氣隙磁密分析

計算兩臺電機氣隙磁場的諧波正弦性畸變率，208極234槽永磁電動機的諧波正弦性畸變率為0.150 5，198極216槽永磁電動機諧波正弦性畸變率0.155 5。可見，208極234槽永磁電動機的氣隙磁密波形正弦性要優于198極216槽永磁電動機。

圖5、圖6為通過Ansoft軟件計算得出的兩種極槽配合電機的齒槽轉矩波形。

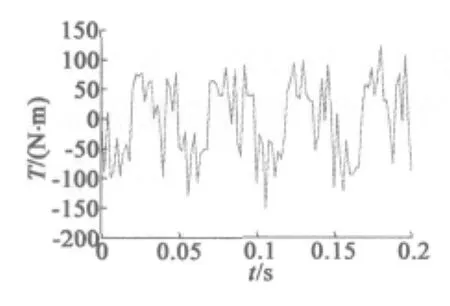
圖5 208極234槽電機齒槽轉矩波形

圖6 198極216槽電機齒槽轉矩波形

由圖5、圖6可以看出，198極216槽永磁同步電動機齒槽轉矩的波動范圍是從－210～280 N·m，而208極234槽永磁同步電動機齒槽轉矩的波動范圍是從－150～125 N·m，明顯低于前者的齒槽轉矩波動。

綜合分析以上兩種極槽配合的方案，最終選擇208極234槽的極槽配合。

2.2 漏磁系數的計算

整數槽電機的漏磁系數可以通過磁場有限元的方法準確求出。但對于分數槽電機尤其是真分數槽電機，通過上述方法求出的漏磁系數誤差較大。真分數槽電機的特點是齒數和槽數的大小相近，這樣就在出現了極間和齒頂兩種漏磁，如圖7所示。

圖7 徑向方向漏磁路分布示意圖

齒頂漏磁的出現增加了電機的漏磁系數，也給電機漏磁系數的準確計算帶來了難度。對于多極少槽的極槽配合可以利用Ansoft求出電機的靜態磁場，再分別求出電機的極間漏磁、齒頂漏磁和電機的總磁通，代入漏磁計算公式求出電機的漏磁系數為1.21。也可以利用Ansoft瞬態場計算出電機的空載反電動勢，再通過公式E0=4.44fKdpNΦδ0KΦ，反推出電機的漏磁系數［3］。圖8為選定永磁同步電動機的空載反電勢波形，通過傅里葉分析可得電機空載反電動勢的基波幅值為120.58 V，再反推電機的漏磁系數為1.20。由于以上分析均采用二維磁場，沒有考慮電機的端部漏磁的影響，所以在選取電機的漏磁系數時要加上端部漏磁系數。最終選取電機的漏磁系數為1.21。

圖8 超低速永磁同步電動機空載反電勢波形

2.3 單邊磁拉力的影響

電機由于加工和安裝的誤差，定、轉子可能不同心，使氣隙磁場中的磁密不相等產生單邊磁拉力。單邊磁拉力作用在定、轉鐵心子上，使鐵心發生變形。所以有必要對電機在受到單邊磁拉力的情況下，定、轉子鐵心發生的變形和受到的應力大小進行分析。

徑向電機單邊磁拉力的計算公式［4］:

式中:β為經驗系數，同步電動機和直流電動機可取0.5;D為轉子鐵心外徑;led為轉子鐵心長度;Bδ為氣隙磁密幅值;e0為初始偏心，計算時可取0.1δ;δ為單邊平均氣隙長度;μ0為真空磁導率。

通過計算得到電機所受的單邊磁拉力為6 137 N。假設單邊磁拉力集中作用在定、轉子相距最近的一條線上，用ANSYS分析這種極限情況時的變形和受力情況如表2所示。

表2 轉子變形量和應力的大小

由以上計算結果可知，轉子厚度為15 mm時的變形量僅為0.007 5 mm。遠小于電機氣隙單邊厚度4 mm的10%，滿足設計要求。

3 電機結構設計

大直徑、多極、超低速座圈電機是將永磁電動機設計成與炮塔座圈相似，炮塔直接與電動機轉子固定，轉子中心軸挖空，轉子轉動直接驅動炮塔旋轉，定子與坦克車體固定不動，連接成一體，定、轉子之間同軸度由大直徑的推力軸承保證。方案設計中的大直徑推力軸承借用了某型坦克上的原車座圈。安裝時，將電動機的空心轉子通過座圈上安裝孔固定在座圈的旋轉面上，定子通過座圈下安裝孔固定在車體上，定、轉子軸向延伸在座圈的下方形成相互作用空間，組成一體后即成為完整的座圈電機。電機與軸承配合的總裝配圖如圖9所示。

圖9 電機與軸承配合總裝配圖

由于電機的直徑大，且轉子為空心結構，故不便安裝電機速度和位置傳感器。解決方案如下:利用原座圈上的齒條，在轉子聯結板上安裝一個彈性齒輪與齒條嚙合，編碼器與齒輪軸相連如圖10所示。彈性齒輪選取18個齒與座圈齒條相配合，當炮塔旋轉時編碼器也同時旋轉，從而獲取速度信息。在電機定子A相繞組軸線處，安裝3個互差120°電角度的霍爾元件，以確定電機起動時轉子的位置。編碼器與霍爾元件的安裝如圖11所示。

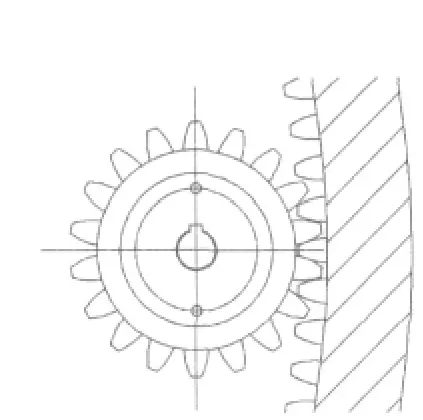
圖10 齒輪與齒條配合示意圖

圖11 編碼器與霍爾元件的安裝示意圖

4 系統控制方案

永磁同步電動機的電磁轉矩主要取決于定子直軸(d軸)和交軸(q軸)的電流分量。由于永磁同步電動機轉子磁鏈不變，所以可采用轉子磁鏈定向方式來控制［5］。為了簡化系統，可把合成電流矢量控制在q軸而無d軸分量，即id=0，iq=i。假設永磁同步電動機各種參數不會隨溫度變化，并忽略渦流、磁滯損耗，且轉子無阻尼繞組，其在d－q坐標系中的定子電壓方程和轉矩方程可以表示如下:

式中:，ud、uq為定子電壓矢量u在d、q軸上的分量，Lq為交軸電感;ω為轉子角頻率;p為微分因子;rs為定子相電阻;p為電機極對數;Ψ為轉子磁鋼在定子上的耦合磁鏈［6］。

從式(1)～式(3)可以看出，只要準確檢測出轉子位置(d軸)，可通過控制逆變器使得三相定子合成電流位于q軸，則永磁同步電動機的電磁轉矩Td僅與定子電流幅值成正比，即通過控制定子電流的幅值，就可以很好的實現對電磁轉矩的控制［7］。

圖12為按轉子磁鏈定向控制(FOC)的永磁同步電動機矢量控制原理圖。

圖12 永磁同步電動機FOC控制原理框圖

根據轉速和轉矩的關系，由參考轉速和電機實際轉速通過速度PID調節輸出得到定子電流的參考輸入。先用Clarke變換將定子相電流ia和ib轉換到定子兩相靜止坐標系中，再用Park變換轉換到d－q旋轉坐標系中。d－q旋轉坐標系中的電流信號與參考輸入量isqref和isdref比較(其中isdref=0)，并通過兩個PI調節器獲得理想的控制量。該控制量再通過Park逆變換作為SVPWM逆變器的輸入，從而得到控制定子繞組的實際電流值。速度環得到定子電流的參考值，電流環產生實際控制量，從而構成了一個完整的FOC雙閉環控制系統［8－9］。

圖12中矢量控制所用到的坐標變換定義如下:

Clarke變換: