穩健時序分析在建筑物沉降監測中的應用

張 瑞 李全海

0 引言

隨著社會的不斷進步和經濟建設的飛速發展，城市中大規模興建了各類建筑物、構筑物，尤其是大量的高層建筑群。各種建筑物的興建，對建筑物的地基增加了一定的荷載，造成地基的變形，這會對建筑物的工作性態產生一定的影響。沉降監測已成為掌握大型建筑物工作性態的基本手段，沉降監測技術的引入對工程的設計和施工的安全穩定起到了不可或缺的作用，而發揮監測作用的核心工作是對動態監測數據的處理。因此，探求動態監測數據處理的方法一直引起人們的極大關注［1］。

時序分析方法所研究的是一系列隨時間變化而又相關聯的動態數據序列，通過對數據進行分析，找出反映事物隨時間的變化規律，從而對數據的變化趨勢做出正確的分析和預報［2］。由于異常值干擾，勢必對監測數據的分析結果造成誤差。為此本文提出基于穩健估計的自回歸建模方法，利用實測數據分析和對比兩種方法。

1 平穩序列模型

在實際觀測的數據中，觀測數據由某種趨勢變化的部分和其他周期變化的部分組成，這時可采用時間序列的分解式表示［3］:

其中，St為變形觀測量序列;μt為趨勢項和周期項;xt為零均值平穩隨機過程。式(1)可通過去除趨勢項和周期項部分將非平穩時間序列轉化為平穩的時間序列。

本文使用差分的方法剔除趨勢項部分，從而平穩化觀測的時間數據序列。

對平穩的時間序列{xt}建立以下方程［4］:

方程(2)稱為自回歸滑動平均模型，簡稱ARMA(n，m)模型。其中，n，m分別為模型的自回歸階數和滑動平均階數;φ1，φ2，…，φn均為自回歸系數;θ1，θ2，…，θm均為滑動平均系數;αt為白噪聲序列。

如果引入延遲算子B，即Bxt=xt－1，則式(2)可簡寫成:

其中，φ(B)，θ(B)分別為自回歸和滑動平均多項式。當ARMA(n，m)模型中的m=0時，θ(B)=1，則可推出n階的自回歸模型，簡稱AR(n):

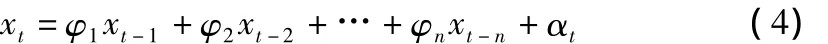
當ARMA(n，m)模型中的m=0時，φ(B)=1，則可推出m階的自回歸模型，簡稱MA(m):

以上三種平穩時間序列模型分別反映了不同時間序列內在的聯系。但考慮到自回歸模型的建模與分析遠比另外兩種模型簡單，通常采用高階自回歸模型近似其他兩種模型。

2 穩健時序分析方法

當樣本數據服從正態分布時，最小二乘估計是無偏、有效的。但測量數據受誤差干擾是難免的，統計學家根據大量數據指出在生產實際和科學實驗中，粗差的出現約占1%～10%［5］。面對具有粗差的樣本數據，最小二乘估計具有一定的負面影響。

穩健估計具有抵抗異常值作用的能力，它利用各種動態權，抵御或降低粗差對結果的影響，減少污染機會，提高穩定性和估值精度。因此，將穩健估計應用于時間序列建模，有望能夠提高建模的精度及可靠性。

基于上述思想和觀測數據一般含有異常值的事實，本文提出了基于穩健估計的AR模型分析方法。

2.1 穩健AR模型

目前，應用最為廣泛的穩健估計是選權迭代法，權函數選取有各種不同的形式。本文選擇常用的Huber權函數，設平穩序列{xt}的樣本觀測值為(x1，x2，…，xN)，再結合自回歸模型式(4)，便可導出基于Huber權函數的穩健AR(n)模型［6］:

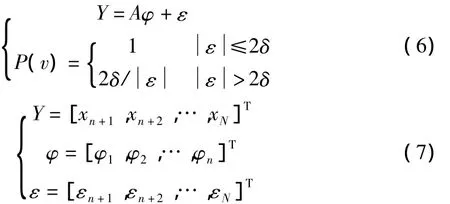
式(6)的基本思想是:從最小二乘進行平差，得到第一組殘差，在每次平差后，根據其殘差與2δ的比較，計算出下次迭代中觀測值相應的權。而含粗差觀測值的權將越來越小，直至趨近于零。迭代中止時，相應的殘差將直接指出粗差的值，而平差的結果也將不受粗差的影響，從而實現粗差的定位剔除。

2.2 參數估計與適用性檢驗

對于常規的時間序列模型的參數估計，一般是利用最優無偏的最小二乘估計。對于自回歸模型R(n)來說，穩健最小二乘估計的迭代計算式是:

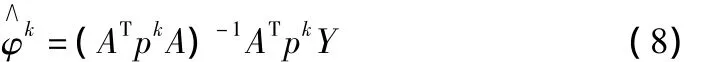
其中，k為迭代次數，每次迭代的權函數不同。當參數估計量的相鄰兩次迭代值相差微小時停止迭代。

為了判定當模型的階數改變時，相鄰階次對應的殘差平方和S(p)的變化是否顯著，可以通過F檢驗法判定。對于AR(p)模型的定階的F檢驗準則是:

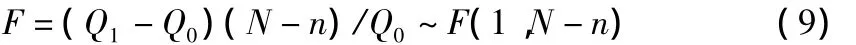
其中，Q0為AR(n+1)模型的殘差平方和;Q1為AR(n)模型的殘差平方和;N為樣本的長度;n為檢驗的階數。給定顯著水平α，查表得Fα。若F≤Fα，則表示模型的階次是合適的(F檢驗不顯著);若F＞Fα，則表示模型的階次是不合適的(F檢驗顯著)增加階次。

2.3 預報與誤差分析

經過上述模型的識別，參數的估計以及定階以后，就可以獲得一個合適的AR(n)模型。根據過去和現在的觀測值，即可對未來可能出現的結果進行數值預報。對時間序列xt所建立的n階的自回歸模型AR(n):

為預報t+l(l=1，2…)期的沉降觀測情況，可利用預報方程［6］:

其中，l，n分別為預報的步數和模型的階次。

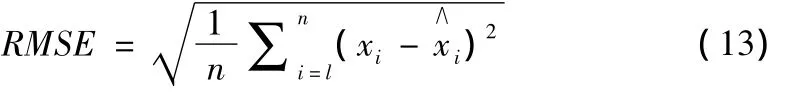
其中，xi， 分別為實測值與預報值。預報中誤差是式中的xi和 分別表示實測值與預報值。

預報中誤差是衡量預報結果偏離實際的指標，該值越大說明預報誤差越大。

3 實例分析

為驗證穩健時序分析方法的可行性，利用某大型倉庫兩個沉降監測點(稱為 A 點和 B 點)連續觀測(2006.9.10 ～2008.1.4)的42期數據進行實例分析。該倉庫共布設了10個沉降監測點，其中以所選的A，B兩點的差異沉降量最大，傾斜率為7‰，超過了相關部門的規定。利用時間序列的方法對A，B兩點的差異沉降量進行分析建模和預報。

將兩測點各期的沉降量相減，獲得差異沉降量序列，由于觀測序列非等時間間距，通過差值預處理，獲得40期等時間間距的時間序列數據，見表1。

表1 A，B兩點差異沉降兩數據(40期) mm

設計方案:取兩點差異沉降量的前35期數據，利用式(4)和式(6)分別建立常規的AR模型和穩健AR模型，其余5組數據用于預報分析的比較。常規的AR模型采用最小二乘參數估計，穩健模型采用式(8)進行參數估計，兩種方法均采用式(9)進行適用性檢驗。

利用上述方案，求得兩點差異沉降量的常規AR模型和穩健AR模型分別為:

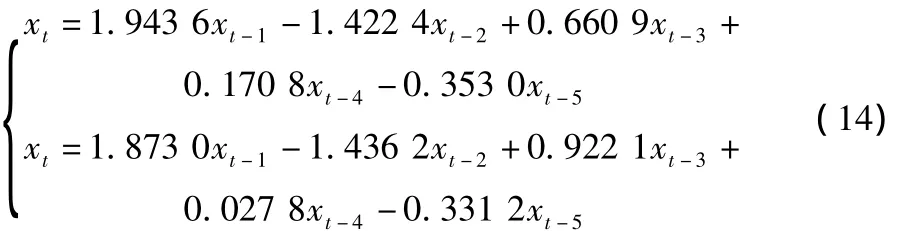
利用式(12)和式(14)中建立的模型，對兩點差異沉降量進行5步預報，并與36期～42期數據進行對比。

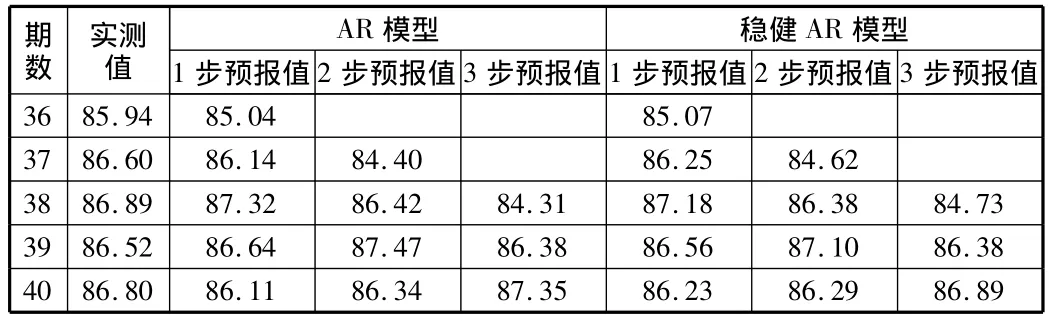
表2 設計方案中兩種模型前三步預報與實測值對比 mm

表2給出了預報值與實測值之間前3步預報的對比。

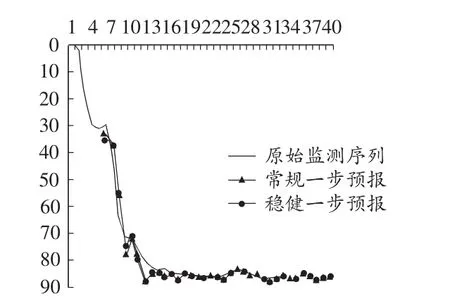
圖1 監測序列及設計方案中一步預報序列比較

圖1是根據設計方案分別顯示了實測序列和兩種時序模型的一步預報序列的變化情況。

為進一步區分常規與穩健AR建模，利用式(12)和式(13)可得本文設計方案中兩個監測點的常規及穩健AR模型的五步預報中誤差，如表3所示。

表3 方案中模型的預報中誤差mm

由表2可知，設計方案中的兩種時序模型的一步預報精度均能控制在亞毫米級，同時結合圖1可知，兩種時序模型的一步預報都能很好的模擬監測數據，能夠達到理想的擬合和預報效果;

由表3不難看出，面對觀測值中無法避免的異常值，穩健AR模型較常規AR模型的相應步數的預報精度有較明顯的提高，穩健AR模型能更好的預報監測點的沉降變化情況;

由表2和表3可知，無論是常規平穩AR模型還是基于穩健估計的AR模型，隨著步數的增加，模型的預報精度明顯下降，這也表明時間序列分析方法比較適用于短期預報。

4 結語

為確保建筑物的運營安全，有必要追蹤監測沉降點的差異沉降量，并建立預報模型。但監測的過程中難免的存在異常值，勢必影響模型分析的結果。本文探討了基于穩健估計的時間序列分析方法，并給出了基于Huber權函數的穩健AR模型。

通過模型預報與監測數據的比較分析可知，面對無法避免的觀測異常值，穩健自回歸模型比常規自回歸模型能更好地反映建筑物實際沉降情況，從而表明提出的穩健AR模型要優于常規AR模型，穩健的時序模型在精密工程測量尤其是變形監測工程中可以有廣泛的應用。

［1］ 劉志強，何秀鳳.穩健時序分析方法及其在邊坡監測中的應用［J］.測繪科學，2007，32(2):40-41.

［2］ 梅 紅，岳東杰.時間序列分析在變形監測數據處理中的應用［J］.現代測繪，2005(8):73-75.

［3］ 陸 立，胡曉麗，王春華.用時間序列分析法進行建筑物沉降觀測數據處理的研究［J］.測繪科學，2004(1):30-31.

［4］ 楊叔子，吳 雅.時間序列分析的工程應用［M］.武漢:華中理工大學出版社，2010.

［5］ Huber P J.Robust Statistics.New York:Wiley，1981.

［6］ 劉大杰，陶本藻.實用測量數據處理方法［M］.北京:測繪出版社，2000.