灰色理論在圍巖變形預測中的應用
解志剛 許海東
1 概述
在預測分析中,最基本的是線性回歸預測,但是在實際工程應用中,我們的數據是非線性的、離散狀態的,隧道圍巖的變形就是一個由復雜因素所決定的非線性的變形,對于隧道圍巖變形的預測中線性預測辦法是不可取的,我們可以應用灰色理論對圍巖的變形進行預測。灰色理論,又稱灰色系統,是指既有已知信息,又包含未知信息的系統;是研究分析、建模、預測、決策、控制的理論。該理論自20世紀80年代創立以來,已經在社會科學和自然科學的許多領域得到了應用。巖石力學中的一些問題,例如上述圍巖變形,具有灰色系統的特點,灰色理論能很好的應用于上述問題。以下將討論利用灰色理論進行圍巖變形的預測。
2 灰色理論的GM(1,1)模型
圍巖變形的測量結果,是一個時間序列數據,通過建立灰色理論模型,來預測未來圍巖變形,以便為工程的設計和施工提供有關的圍巖動態信息。首先討論GM(1,1)模型問題。
2.1 建立 GM(1,1)模型
假定在時間序列 t1,t2,…,tn,量測的圍巖變形為數列 x1,x2,…,xn,記為:
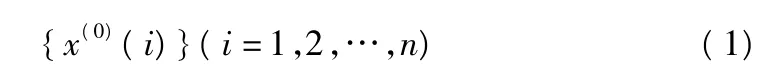
此為原始數據,為了弱化原始數據的隨機性,對原始數據做累加,也就是它的1-AGO,得到數列:
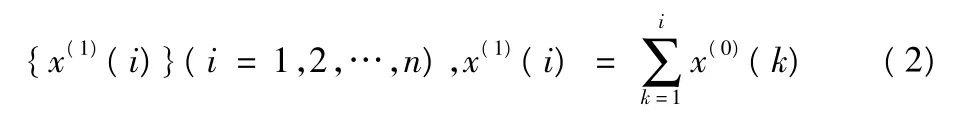
由原始數據(1)和累加數據(2)可以分別得到向量Y和矩陣B:
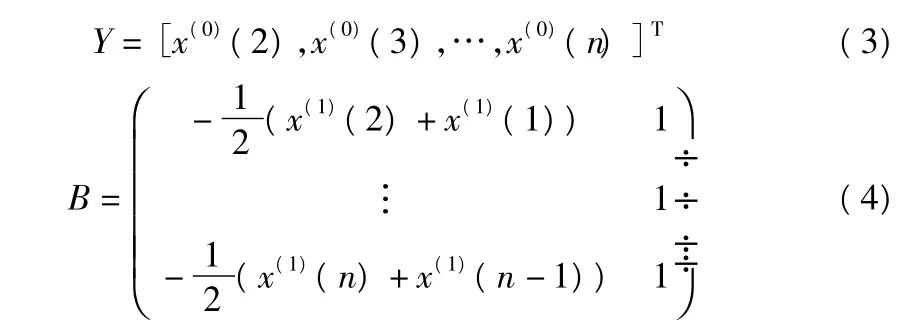
對于GM(1,1)模型,相應的白化微分方程為:

該微分方程的解為:
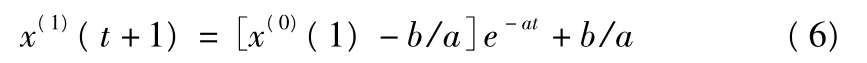
其中,a,b均為待定系數,一般記為 A=[a,b]T。
對于微分方程(5),其待定系數A=[a,b]T的最小二乘法解為:
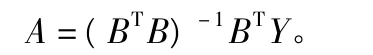
將原始數據x(0)(i)和累加數據x(1)(i)代入式(7)中,可以得到a,b值。我們可以通過式(6)進行預測。
2.2 GM(1,1)模型的精度
以上我們介紹了灰色理論模型的建立方法,下面我們要根據解式(6)計算殘差:
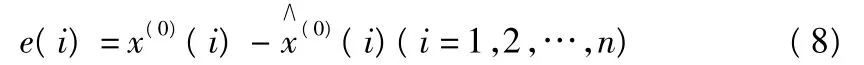
得到殘差向量和相對誤差分別為:
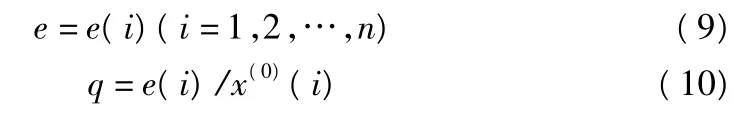
設原始數據的方差及殘差向量的方差分別為s21和s22,則:
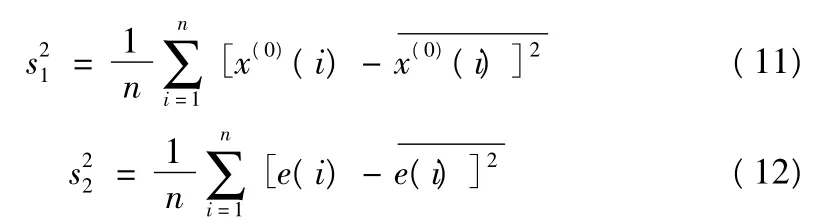
方差比值Q為:

小誤差概率為:

模型的精度由Q和P來控制和表述,一般將其分成四級,見表1。通過計算所得P值或Q值來劃分等級,評價預測精度的好壞。

表1 預測精度等級劃分
2.3 基于灰色預測的等維灰數替補迭代
為了進一步提高模型預測的精度,在灰色模型的基礎上還可以做進一步的改進,使得預測結果更加準確。GM(1,1)模型具有預測意義的數據僅僅是x(0)(i)以后的前幾位數或者∧x(0)(i)數列的前幾位數,隨著時間的推移,舊的數據越來越不適應新的情況,所以,要在原數據的基礎上每次增加一個新信息時,就去掉一個舊信息。這種新數據補充、舊數據除掉的數列,由于維數沒有變,因而叫等維灰數數列或者叫新陳代謝數列。利用新的數列重新建立GM(1,1)模型,對下一個新數據進行預測,預測完畢后,再次生成新的數列。這樣就類似于迭代原理,我們可以通過數值計算來實現GM(1,1)模型的生成和迭代,這樣的改進可以保證精度的良好性。
3 利用GM(1,1)模型預測隧道圍巖的變形
以武廣高速鐵路衡陽段胡子沖隧道為例,隧道的圍巖以花崗巖為主,地下水豐富,地形比較復雜。隧道初期支護的噴射混凝土厚度為25 cm,我們在隧道開挖過程中對DK091+124斷面拱頂圍巖變形進行了監測,監測數據見表2。
GM(1,1)模型的建立,是在取得一定數據之后進行的,建模以后就可以對未來變形進行數據預測。由于收斂變形是持續進行的,因此,不斷有新的數據充實變形時間序列,考慮到現場的條件不斷變化,前期測量的數據對后期研究圍巖的變形有一定的作用,但是越是接近于預測時間的量測數據越有意義(見表3)。因此,我們采用GM(1,1)迭代模型來進行預測,預測后我們可以對預測和實測數據進行比較(見圖1)。
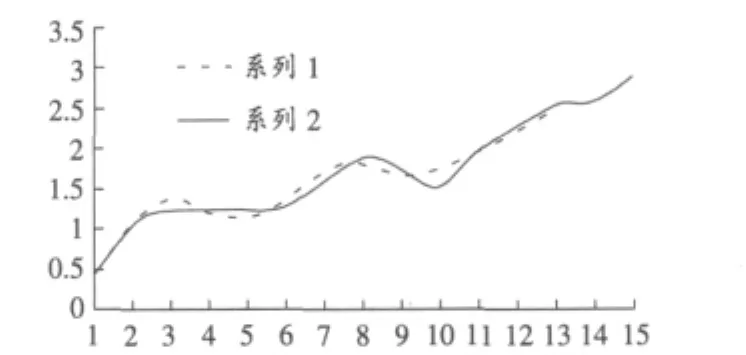
圖1 實測與預測數據對比圖

表2 監測數據

表3 GM(1,1)模型的預測值
經過對殘差的計算,本例中的GM(1,1)模型的精度達到了Ⅰ級,所以預測的數據與實際數據還是比較吻合的。
通過計算我們可以判斷在4 d以后圍巖穩定,在50 d左右變形加大,這時胡子沖隧道進尺達到56 m,應該進行二次支護或者應停止開挖,以保證隧道施工的安全。同時我們使用有限元軟件對胡子沖隧道進行了施工模擬,通過模擬可以知道在隧道進尺60 m左右時必須進行二次支護,模擬過程這里不再贅述。從這里可以看出利用灰色理論進行隧道圍巖變形的預測在實際工作中是有很大意義的。
4 結語
本文通過以胡子沖隧道的圍巖變形預測為例,對灰色理論在圍巖與初期支護相互作用變形預測的應用進行了闡述。灰色系統理論有著廣泛的應用前景,將其用于分析和處理圍巖的變形預測是一種行之有效的方法。通過上述分析和論述,我們可以得出以下結論:
1)利用GM(1,1)模型對變形進行預測方便之處是實測數據需要很少(灰色理論并不因為實測數據多而變得精確度高),并且預測數據的精度高,對于普通回歸方法則要更多的數據來預測,而且灰色理論能對一些非線性或者不確定的因素進行弱化,以提高預測的準確性。2)收斂變形的時效性動態表明,預測變形必須時時更新,而灰色理論預測恰恰能解決這個問題,這與以往回歸方法不同,這樣能更加有利于隧道施工中的變形監控(施工要求時時監測圍巖變形,已確定圍巖變形的穩定情況)。3)從取得原始數據到建立GM(1,1)模型,計算量還是比較大的,但是我們可以在計算機上利用數值計算方法輕松完成建模和迭代計算。因此,用灰色理論來分析圍巖變形資料,預測圍巖收斂變形以及判斷可能失穩的前兆及時間是有工程實用意義的。
[1] 張忠亭,陶振宇.洞室圍巖收斂變形的時間效應特性研究[J].武漢水利水電學院學報,1995(12):89-92.
[2] 鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.
[3] 熊合金,徐華中.灰色控制[M].北京:國防工業出版社,2005:9.
[4] 解 偉.灰色預測和灰色關聯度在結構可靠度中的應用[J].華北水利水電學院學報,2005(6):20-25.
[5] 劉法貴.灰色數學及其應用[M].開封:河南大學出版社,2002:21-88.

