局域均值分解在MEMS陀螺隨機誤差消噪上的應用

李 軍， 朱家海， 謝 聶， 郭明威

(空軍工程大學工程學院，西安 710038)

0 引言

近年來，微機械電子系統(Micro Electronic Mechanical System，MEMS)陀螺因其具有成本低、體積小、重量輕、集成度高等突出優點，已在汽車導航、消費電子、短程武器制導等領域得到廣泛應用。MEMS陀螺的隨機漂移誤差嚴重影響了陀螺的精度，又往往表現為非平穩性、弱線性、慢時變的特性，所以選用有效的濾波方法來提高測量精度顯得尤為重要［1］。

抑制MEMS陀螺隨機誤差的方法通常有3種［2］。1)對MEMS陀螺的隨機誤差信號進行時間序列分析，建立模型。依據模型設計Kalman濾波器，通過Kalman濾波來減小隨機誤差。2)采用低通濾波器抑制高頻噪聲。3)基于小波變換，小波閾值去噪。

但在實際情況下，MEMS 陀螺受多種誤差因素制約，難以建立準確的隨機誤差模型，采用第一種濾波方法效果有限。由于陀螺有用信號與噪聲信號存在交疊頻帶，第二種方法也存在固有的缺陷。小波變換雖具有良好的時頻局部化特性，能實現信號在不同頻帶、不同時刻的分離，具有良好的去噪效果，但小波閾值消噪的性能對于小波基選擇、分解層數、閾值選取準則和閾值依賴層數等因素的依賴性較大，需多次調試，缺乏自適應能力。

針對上述信號濾波方法存在的缺陷，論文引入局域均值分解(LMD)［3］，將其與小波方法結合用于MEMS陀螺隨機誤差濾波。該方法不用建立隨機誤差模型，無需多次調試，一步到位，具有良好的自適應能力。

1 信號的局域均值分解

Smith于2005年提出了局域均值分解方法(Local Mean Decomposition，LMD)，這種區別于 EMD［4－5］的時頻分析方法將復雜的非平穩信號分解為若干個乘積函數(Production Function，PF)的線性組合，PF表示信號中某一頻率段的諧波信號，表征了其頻率和幅值。每一PF分量由一個包絡信號和一個純調頻信號相乘而得到，包絡信號是該PF分量的瞬時幅值，而PF分量的瞬時頻率則可由純調頻信號直接求出，迭代分離出所有PF分量，即可得到原始信號的時頻分布。對于原始信號x(t)的LMD分解過程如下:

1)確定原始信號所有極值點，任意兩個相鄰極值點的平均值即定義為局域均值，則第i段的局域均值函數值為

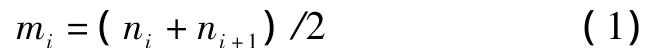
相鄰兩極值點差值的1/2定義為局域包絡函數，則第i段局域包絡函數值為

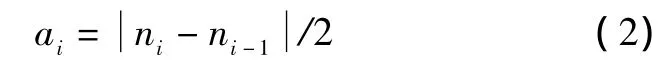
2)對局域均值函數和局域包絡函數用滑動平均法處理［6］，得到局域均值函數m11(t)與局域包絡函數a11(t);

3)將局域均值函數m11(t)從原信號中分離出來，得到

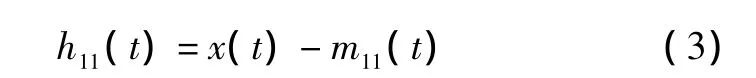
用h11(t)除以局域包絡函數a11(t)，對h11(t)解調，得到

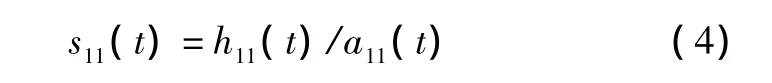
對s11(t)重復上述步驟得到s11(t)的局域包絡函數a12(t)，若a12(t)=1，則已經是調頻信號，否則將s11(t)作為原始數據重復以上迭代過程，直到s1n(t)為一個調頻信號，即它的局域包絡函數a1(n+1)(t)=1時為止;

4)把迭代過程中產生的所有包絡估計函數相乘便可以得到包絡信號(瞬時幅值函數)。

將包絡信號a1(t)和純調頻信號s1n(t)相乘便可得到原始信號的第一個PF分量

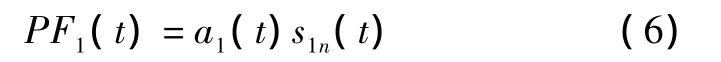
它包含了原始信號中最高的頻率成分，是一個單分量的調幅－調頻信號，其瞬時幅值就是包絡信號a1(t)，其瞬時頻率 f1(t)則可由純調頻信號求出［6－7］，即

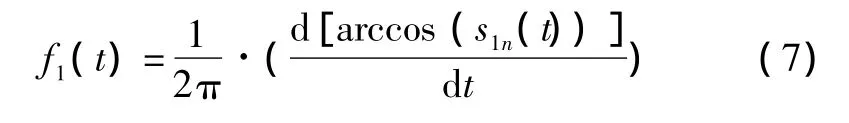
將第一個PF分量PF1(t)從原始信號x(t)中分離出來，得到一個新的信號u1(t)，將此信號作為原始數據重復以上步驟，循環k次，直到uk(t)為一個單調函數時為止，這樣便可以將x(t)分解為k個PF分量和一個單調函數uk(t)之和，即

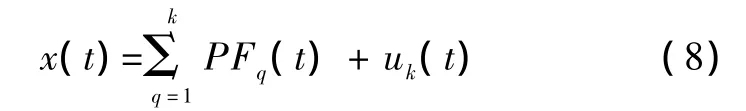
由此可見，LMD分解沒有原信號信息的丟失。

2LMD降噪應用

小波閾值濾波是一種比較有效的濾波方法，其原理是通過在不同尺度上選取一合適的閾值，從帶噪的信號中恢復出原信號。基本步驟為:1)選擇合適的小波基和小波分解層數，對含噪聲信號進行小波分解，得到相應小波分解層數;2)對分解后的小波系數進行閾值處理，得到原始信號的小波系數估計值;3)對估計的小波系數進行小波重構，得到去噪后的信號。上述的步驟中，最關鍵的是如何選取閾值和閾值的量化，它直接關系到去噪的效果［1，8］。

由于小波閾值降噪效果取決于小波基、分解層數、閾值選取準則的選擇等，缺乏自適應能力，本論文首次將LMD與小波方法綜合應用于MEMS陀螺濾波，增強對隨機噪聲的自適應濾波能力。MEMS陀螺降噪步驟如圖1所示。

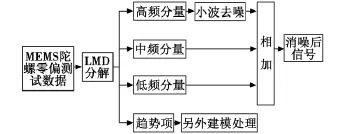
圖1 LMD降噪應用的步驟圖Fig.1 De-noising method based on LMD

LMD可自適應分解出滿足從高頻到低頻分布的PF分量，無需確定分解層數。而且對分解后的PF分量運用小波去噪時，由于各分量的頻帶已較窄，小波基、分解層數等對去噪效果的影響就非常有限。MEMS陀螺的噪聲多數分布在中高頻帶，如果不加判別標準，可以通過觀察將視為噪聲的中高頻PF分量直接舍棄，重構原信號達到降噪目的，但是這樣會損失可能存在于中高頻分量中的有用信息，所以對中高頻帶PF分量采用小波降噪獲得降噪后的數據與不含噪聲的低頻PF分量一起構造原信號，這樣小波閾值降噪僅僅作用于中高頻PF分量，而不是直接作用于整個信號，在很大程度上克服了小波閾值降噪的缺陷。

3 實驗分析

一般認為，陀螺漂移是一弱線性、非平穩的隨機過程，前述濾波方法非常適合處理類似信號。下面將針對實測數據用此方法濾波。

在常溫(20℃)對ADXRS300做了零漂測試。在該陀螺啟動一小時后開始采樣，采樣頻率100 Hz，采樣時間4500 s。其零漂測試曲線如圖2所示，可看出該曲線存在明顯的趨勢項。

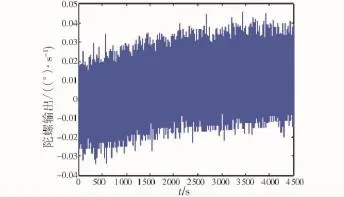
圖2 陀螺輸出原始信號Fig.2 Original output signal of MEMS gyro

MEMS陀螺精度不高，只適合于短時間工作，因此應當著重研究其短時的漂移特性［9］。為此，本文截取開始測試后30～70 s時間段的數據進行分析。

30～70 s段數據如圖3所示，對其進行LMD分解，分解所得各分量與趨勢項如圖4所示，可以看出:該信號經過LMD分解成7個PF分量和一個趨勢項，7個分量由高頻至低頻系列分布，其趨勢項為單調函數，可判定為非隨機噪聲，另對其建模處理，在重構信號時將其直接舍棄。

圖3 30～70 s數據Fig.3 Data of 30 s to 70 s

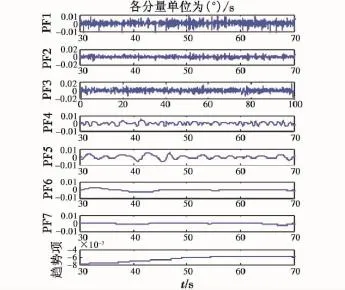
圖4 LMD分解PF1～PF7分量及趨勢項Fig.4 PF1 ～ PF7 and the trend of LMD

采用前述濾波方法，對PF(1－2)采用小波降噪，舍棄趨勢項，重構后得到消噪信號。消噪效果如圖5所示。可發現:消噪后的信號已沒有明顯的趨勢項，方差為原信號的23%，效果較為理想。

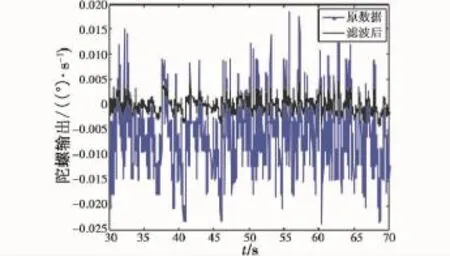
圖5 基于LMD的小波濾波前后對比圖Fig.5 De-nosing results based on LMD

LMD與小波降噪結合可大大提高濾波的自適應能力。此外LMD還可應用于Kalman濾波前的數據預處理，不僅能剔除趨勢項，還可對分解所得到的趨勢項建模以便進行補償。

傳統的陀螺漂移模型為:陀螺漂移=趨勢項+零偏+周期項+ARMA模型［10］。在進行Kalman濾波前需對數據預處理以建立ARMA模型［9］。所以在數據預處理中，一項重要的工作就是要去除趨勢項，使數據平穩化。常用的多項式擬合法當趨勢項不規則時，擬合的階次難以選擇，去除效果也不太理想。由LMD分解原理可知，如果信號中有趨勢項，則一定存在于殘余分量中或低頻的PF分量中。在信號重構時舍棄殘余分量和被判定為趨勢項的低頻PF分量，則去除了信號中趨勢項，避免了多項式擬合法的階次選擇問題。

4 結論

針對MEMS陀螺的噪聲特性，為克服傳統濾波方法的不足，提出了基于局域均值分解與小波去噪綜合應用的方法，對陀螺隨機信號進行濾波處理。經過比較分析:與傳統方法相比，基于局域均值的濾波方法不僅能夠有效去除噪聲，而且具有信號處理的穩定性和自適應性，避免了Kalman濾波的建模過程和小波消噪中參數選取的繁瑣過程，具有較強的實用價值。

［1］杜繼永，黃國榮，程洪炳，等.基于改進小波閾值法處理MEMS陀螺信號噪聲［J］.電光與控制，2009，16(12):61-64.

［2］曲從善，于鴻，許化龍，等.基于經驗模態分解的激光陀螺隨機信號消噪［J］.紅外與激光工程，2009，38(5):859-863.

［3］SMITH J S.The local mean decomposition and its application to EEG perception data［J］.Journal of The Royal Society Interface，2005，2(5):443-454.

［4］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and norstationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454:903-994.

［5］HUANG N E，ATTOH-OKINE N O.The hilbert huang transform in engineering［M］.Boca Raton:Taylor＆ Francis Group，2005.

［6］任達千，楊世錫，吳昭同，等.基于LMD的信號瞬時頻率求取方法及實驗［J］.浙江大學學報:工學版，2009，3(3):523-528.

［7］程軍圣，張亢，楊宇，等.局部均值分解與經驗模式分解的對比研究［J］.振動與沖擊，2009，28(5):13-16.

［8］李振興，徐洪州.基于經驗模態分解的小波閾值降噪方法研究［J］.計算機仿真，2009，26(9):325-328.

［9］張海鵬，房建成.MEMS陀螺儀短時飄移特性實驗研究［J］.中國慣性技術學報，2002，15(1):100-104.

［10］張海鵬，房建成，盛蔚.石英MEMS陀螺漂移的周期性誤差標定及補償［J］.北京航空航天大學學報，2007，33(12):1412-1416.