商業銀行操作風險傳導計量研究*

李曉蓓 費倫蘇 戴勝利

（1、武漢理工大學管理學院 湖北 武漢430070；2、華夏銀行總行綜合個人信貸部 北京100005；3、華中師范大學管理學院湖北 武漢 430079）

隨著2006年底中國銀行業的全面開放，行業競爭不斷加劇。國內商業銀行為了應對競爭，不斷推出新產品與新業務來爭奪客戶市場，商業銀行面對的與之相伴的的各種風險威脅不斷增長。此外，國內監管與國際監管的接軌和新法規的實施，都使商業銀行面臨更多的法律和監管風險。因此，風險管理成為當前中國商業銀行經營管理中的關鍵議題。商業銀行的風險管理問題中，尤其以動態的風險傳導問題最為復雜，而風險傳導的計量問題也一直是商業銀行風險管理中的一個難題，國內外很多學者對其進行了研究。

一、國內外相關研究

（一）國外相關研究 Duncan Wilson（1995）認為，操作風險可以應用VAR來進行度量，商業銀行可以利用內部和外部數據建立操作風險損失事件數據庫，描繪出操作損失的概率分布，從而計算出在一定置信水平下的操作風險VAR。但Wilson同時也認為，使用VAR仍然需要進行壓力測試和情景分析，他建議使用定量與定性相結合的“混和方法”，將相對風險排序和“專家組”方法的使用與基于損失事件數據庫的建模技術結合起來；Douglas和Hoffman（1996）指出，將操作風險視作商業銀行的分散資源的所有方向——客戶關系、職員、物質設備、財富和資產等銀行負有責任的資源和技術資源，操作風險還包括特定的外部因素，如監管風險和欺詐風險；Alexander J.McNeil（1999）分析了極值理論在操作風險量化管理中的應用，但他只進行了理論分析，沒有提出具體的操作風險管理對策；而Elena Medova（2003）分析了極值理論在操作風險資本配置中的作用；JunjiHiwatashi（2002）介紹了日本先進銀行的操作風險度量技術的最新進展，總結了這些銀行操作風險管理的成功經驗；John Jordan，Eric Rosengren與Reimer Kuhn（2003）提出了基于VAR模型的銀行操作風險資本金需求的計算方法；Dr.Mark Lawrence（2003）分析了在內部數據充足和不足的情況下如何運用損失分布法來進行操作風險資本要求的測算，為商業銀行測算操作風險資本提供了思路；Cruz，M（2000）開發了一個評估操作風險的模糊邏輯系統；Jack.LKing（2003）提出了Delta-EVT模型，從理論上分析了如何運用Delta因子來測算“高頻低危”事件的損失，以及如何運用極值理論（EVT）進行“低頻高危”事件的操作風險計算；2004年5月巴塞爾銀行監督管理委員會在廣泛咨詢各方意見和進行多次定量調查以后，提出了三種計量操作風險資本的方法，即基本指標法、標準法和高級計量法。而在高級計量法中，又分為內部衡量法、損失分布法和記分卡法。

（二）國內相關研究 國內學者也對商業銀行的風險計量問題進行了相關研究。沈沛龍等（2002）對新巴塞爾協議中關于操作風險資本金計算的理論依據和計算框架進行了剖析；全登華（2002）則介紹了極值理論和POT模型在計量操作風險VAR方面的應用及優缺點；田玲等（2003對衡量操作風險的基本指標法、標準化方法、內部衡量法、損失分布法和極值理論模型進行比較分析，探討現階段中國商業銀行應選擇的操作風險度量模型，并認為操作風險模型化的趨勢應與加強操作風險管理有機結合起來；陳學華（2003）探討了VAR模型在商業銀行操作風險度量中的應用，說明POT模型的優點在于可以準確描述分布尾部的分位數，具有解析的函數形式，計算簡便；鐘偉（2004）介紹了損失分布法與高級衡量法在操作風險度量中的應用，指出歷史數據、損失類型相關程度低及尾部特征難以量化是損失分布法在應用中面臨的難題，并對應用高級計量法的難點和挑戰進行簡要闡述；唐國儲等（2005）討論了在商業銀行內部如何執行LDA，同時按照巴塞爾協議公布的方法和策略，從損失事件類型、業務部門以及損失分布額度的估計方法探討利用高級度量方法的可能性和現實性以及操作中的現實問題；梁繽尹（2005）指出，處于不完善的制度環境中的我國銀行采取內部模型測量操作風險是加強銀行自律的有效前提，并針對操作風險衡量的復雜性，設計了基于信息熵的操作風險計量改進模型。綜合國內外相關研究，學者們對商業銀行的風險計量問題做了很多有益的探討，但相關討論大都是針對商業銀行的操作風險計量展開的，而對商業銀行操作風險傳導考慮較少。

二、商業銀行操作風險傳導衡量的方法分析

（一）概率法 概率法包括客觀概率法和主觀概率法。在大量的試驗和統計觀察中，一定條件下某一隨機事件相對出現的頻率是一種客觀存在，這個頻率稱為客觀概率。人們對某一隨機事件可能出現的頻率所做的主觀估計，就稱為主觀概率。在估計某種金融損失發生的概率時，如果能夠獲得足夠的歷史資料，用以反映當時的經濟條件和金融損失發生的情況，則可以利用統計的方法計算出該種金融損失發生的客觀概率，這種方法稱為客觀概率法。主觀概率法是由商業銀行操作風險機構選定一些專家，并擬出幾種未來可能出現的經濟條件提交給各位專家，由各位專家利用有限的歷史資料，根據個人經驗對每種經濟條件發生的概率和每種經濟條件下發生金融損失的概率作出主觀估計，再由商業銀行操作風險分析機構匯總各位專家的估計值進行加權平均，根據平均值計算出該種金融損失的概率。這種方法的運用，可以在三個層面開展：從商業銀行操作風險的風險源出發，用統計方法進行概率分析，找出易發風險源；從商業銀行操作風險的風險載體出發，用統計方法進行概率分析，找出易發風險載體；從商業銀行的操作風險路徑出發，用統計方法進行概率分析，找出易發的風險環節。通過在這三個層面的工作，用概率的方法，能夠判斷商業銀行操作風險傳導的程度。

（二）統計估值法 利用統計資料，可以確定在不同經濟條件下某種風險發生的概率；或是在不同風險損失程度下，某種風險發生的概率。風險傳導衡量的一個重要方面是根據風險傳導的概率分布預測未來損失發生的頻率和程度。損失的概率分布包括：

（1）離散型概率分布。只有有限或可數個可能值的變量稱為離散型變量。假設X1，X2，…，Xn是變量X的n個觀測值，其一切可能值a1，a2，…，anvi（i=1，2，…，r）wi=vi/ni，那么稱vi為n次觀測中ai出現頻數（Frequency number），稱wi為ai出現的頻率（Frequency Rateor Relative Frequency），稱Fi=w1+w2+…+wi（i=1，2，…，r）為累積頻率（Cumulative Frequency）。那么，變量X的頻率分布由如下統計表表示見（表1）。（表1）給出了離散型頻率分布的一般形式，其中第一行和第二行稱作頻數分布，第一行和第三行稱作頻率分布，第一行和第四行稱作累積頻率分布。頻率還可以用頻率分布縱條圖表示，見（圖1）。

（2）連續型概率分布。連續型變量的值域是直線上有限或無限區間，其值有無限多個且不可數。假設X是一個連續性變量，X1，X2，…，Xn，Xn是對變量X的n個觀測值，［u1，u2］，［u2，u3］，…，［ur，ur+1］是統計分組，那么，連續型頻率分布的一般形式如（表2）。離散型變量分布對任意的整數x都有一個對應的概率值。連續型變量分布要對每一個不同金額的外匯收入損失顯示其概率是不可能的，只能對一定范圍的數值來表示其概率大小，亦即將其分組，然后確定每組對應的概率。

（3）二項分布。二項分布是由貝努里試驗推導出來的一種重要的離散型概率分布，滿足下列五個條件的隨機試驗稱為貝努里試驗：第一，每一次試驗有兩種可能結果，即A或B，如果A出現，B就不會出現；第二，試驗結果對應一個離散型隨機變量；第三，試驗可以在同樣的條件下重復進行；第四，各次試驗出現A的概率是p，事件B不會出現的概率是q，q=1-p；第五，各次試驗的結果相互獨立。重復進行n重貝努里試驗中的A事件發生的次數，則X是一個隨機變量，它所有可能的取值為0，1，2，…，n的分布形式為：

表1 離散變量的頻率分布

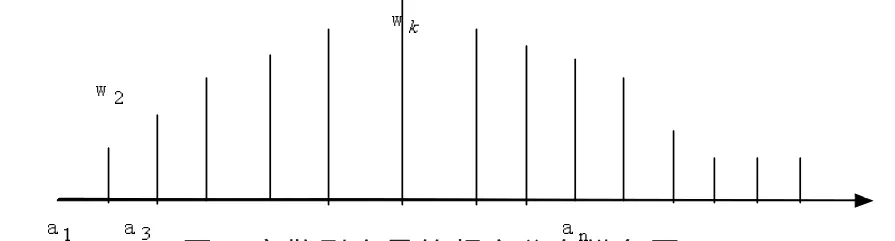
圖1 離散型變量的頻率分布縱條圖

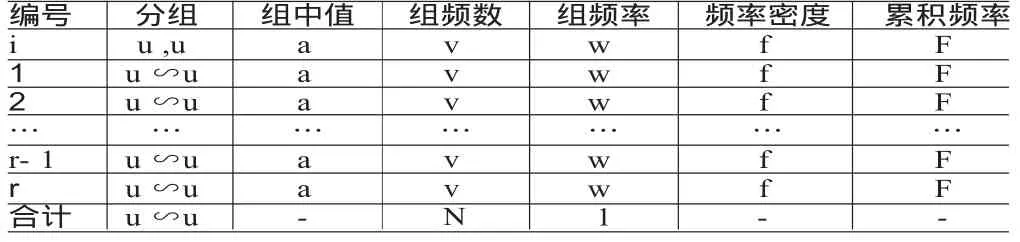
表2 連續型頻率分布的一般狀況

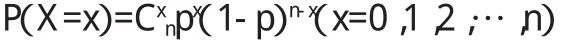
這樣X就服從參數n、p的二項分布。其中，p（X=x）為A事件發生x次的概率；p為A事件發生的概率；n為試驗次數；x為A事件發生的次數（0≤x≤n）；q=1-p

根據二項分布公式及離散型隨機變量的數學期望與方差公式，可得出二項分布的數學期望與方差：μ=E（x）=np；σ2=D（x）=npq。

如某地區8種商業銀行操作風險中有5種風險發生了傳導，某金融企業存在4種較顯著的商業銀行操作風險，這4種商業銀行操作風險可能有2種發生風險傳導的概率為

（4）泊松分布。當試驗次數n很大時，用二項分布計算發生的概率很麻煩，對于這種情況可以采用泊松分布作近似計算。事實上，當p（p≤0.1）較小時，甚至不必n很大，這種近似計算的效果非常好。如果隨機變量X的分布為

這樣可以稱隨機變量X服從參數x的泊松分布。其中，x為某一事件在某一空間或時間范圍內發生的次數；e為常數，e=2.71828；為隨機事件在單位空間或時間間隔內發生的次數。

泊松分布的數學期望與方差均為λ，μ=E（x）=λ，σ2=D（x）=λ。泊松分布是風險衡量中非常有用的概率分布，風險管理實務中許多事故往往以泊松分布的方式發生。使用泊松分布來描述商業銀行操作風險傳導的概率時，說明商業銀行操作風險的種類雖然較多，但風險傳導的概率較小，可以采用泊松分布的概率計算風險傳導的頻數和頻率。

（5）正態分布。隨著觀察次數的增加，二項分布就有可能近似于正態分布，正態分布是一種連續型隨機變量的概率分布，正態分布的使用條件是：如果存在多個隨機因素，每一個因素都不占主導地位，則隨機變量服從正態分布。

則稱X服從正態分布。其中，f（x）為隨機變量C的概率密度函數；σ2為方差；μ為數學期望值。由正態分布的概率密度可以得出分布函數

如果隨機變量X表示風險所致的損失，則根據正態分布函數可以估算出：損失落在［μ-σ］與［μ+σ］之間的概率；損失落在［μ-2σ］與［μ+2σ］之間的概率；損失落在［μ-3σ］與［μ+3σ］之間的概率。正態分布是風險傳導的概率分布中較為常見的一種。隨著近年來金融危機傳染效應的增強，風險傳導數量（隨著金融危機爆發次數的增加）也在增加，滿足正態分布的要求，可以說風險傳導具有正態分布的特征。正態分布是完美的鐘形見（圖2）。

（三）信貸風險模型估計法 Credit Risk模型由Credit Financial Products（CSFP—瑞士信貸銀行金融產品部）開發，其基本思想來自保險業，用于衡量被保事件的發生頻率和事件發生后損失的價值（即損失的嚴重性）。將該模型用于風險傳導，可用來衡量風險傳導及傳導的嚴重性的聯合分布，如（圖3）所示。若單筆風險傳導概率較低且商業銀行操作風險組合中各種風險傳導概率相互獨立，則可以認為其符合泊松分布，即可以根據泊松分布計算出風險傳導率的頻率。

商業銀行操作風險傳導問題是目前商業銀行風險管理中一個熱點問題，也是難點問題，尤其是商業銀行操作風險傳導量的衡量，本文通過對國內外相關文獻的研究，結合其他學科的方法和技術，提出概率法、統計估值法、信貸風險模型估計法三種用于衡量商業銀行操作風險傳導量的方法，為進一步研究商業銀行操作風險傳導的控制與管理提供幫助。

圖2 正態分布曲線

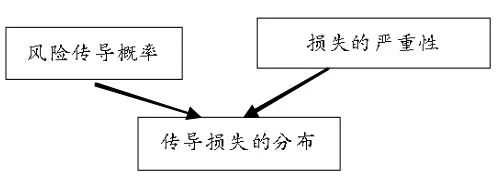
圖3 Credit Risk模型

［1］沈沛龍、任若恩：《新巴塞爾協議資本充足率計算方法剖析》，《金融研究》2002年第6期。

［2］陳學華等：《POT模型在商業銀行操作風險度量中的應用》，《管理科學》2003年第2期。

［3］唐國儲、劉京軍：《損失分布模型在操作風險中的應用分析》，《金融論壇》2005年第9期。

［4］John Jordan，Eric Rosengren and Reimer Kuhn.Using Loss Datato Quantify Operational Risk，Working Paper of Federal Reserve Bank of Boston.2003.

［5］Cruz，M，Applicationof Fuzzy LogictoOperational Risk，2000.

［6］Jack LKing.Operational Risk：EVTModels，Newyork：American Risk and Insurance Association，2003.