基于模糊聚類的交通小區劃分方法研究

劉乙霏 （上海海事大學 經濟管理學院，上海 200135）

基于模糊聚類的交通小區劃分方法研究

劉乙霏 （上海海事大學 經濟管理學院，上海 200135）

闡述了交通小區的定義，劃分交通小區的目的與原理，依據模糊聚類分析法，運用MATLAB軟件進行聚類分析，提出整合方案。

交通小區；模糊聚類分析法；MATLAB

1 交通小區概念

交通小區是具有一定交通關聯度和交通相似程度的節點或連線的組合，隨時間、關聯度和相似度的變化而變化，反映了城市道路網交通的時空變化的特性[1]。

2 交通小區劃分的目的和原理

在交通規劃領域中提出了劃分交通小區。交通小區是指研究交通生成與分布的基本空間單位。劃分交通小區是交通調查與規劃中最基本的工作。其主要目的是在滿足精度要求的情況下，強調交通調查的實際可操作性，盡可能減小交通調查的工作量，降低交通分析和預測的難度；交通需求量可以在交通小區的分布圖上動態地顯示出來，可以直觀的反應交通需求分布，從而為城市道路網絡的交通流提供數據，進而運用交通分配理論模擬道路網上的交通流。

交通小區的劃分遵循以下原則：

·保證小區內土地利用、經濟社會指標的一致性，不應打破城市行政區的劃分；

·盡量將鐵路、河川等天然屏障作為分區界限，避免小區內存在的自然或人為的障礙線；

·小區形狀盡量為規則形狀；

·應充分考慮城市道路網結構，盡可能使小區劃分與道路網協調一致；

·盡可能使交通小區出行中心位于路網節點 （交叉口和干道）上；

·不以干道作為劃定小區的界線，盡可能使道路兩側同在一個交通小區，以便于資料收集整理；

·劃定區內的出行次數盡可能不超過全區域內出行總數的10%～15%。

3 傳統交通小區劃分的理論分析

從根本上講，劃分交通小區范圍大小與小區數目取決于不同性質的OD調查工作所要求的精準程度。已往的交通小區劃分中，主要運用目標層次分析法確定交通小區的劃分。即針對不同目標層次路網的OD調查，對交通小區劃分提出不同要求。

按照行政區域劃分交通小區：

·為大城市和國道干線路網規劃收集數據而進行的路網OD調查工作，要求調查結果反映出大型城市、首府和行政中心等節點的交通連通性時，需要將交通小區的范圍設置的大些，但必須保證交通小區劃分到研究目標城市的下一級城市的節點區域。如果研究區域內一些經濟較為發達、交通矛盾較為突出的地區，為提高工作的精度應將小區劃分的更細。

·為研究中等城市和省級道路規劃收集數據而進行的路網OD調查工作，所劃分交通小區的數目需要大于或等于研究區域內所有的區的數目。

·為區一級行政單位做路網規劃收集數據而進行的OD調查工作，原理上應將居住小區和主要單位劃分為不同的小區，實際中，這樣做會增加無謂的工作量，并且得不出有效的數據，因此，交通小區的劃分應以居住區和主要單位為初步方案，然后針對其中相鄰，居民出行分布類似的居住區和單位進行合并。

還可以按照影響因素的不同劃分交通小區。影響交通小區劃分的因素如下：

·用地性質

用地性質對居民的出行特征產生直接的影響，不同的用地性質會導致不同的交通出行特點。

·交通復雜程度

交通小區如果處于研究區域內部，應在面積、人口與交通發生量與吸引量之間保持適當的均勻性；交通小區如果處于研究區域外部，應隨著與對象區域距離的加大，逐漸增大交通小區的規模，以減少不必要的工作量。

·自然地貌

在一般情況下，山川等自然障礙物被作為行政區劃分界線使用，因此這與第一條并不矛盾。

4 模糊聚類分析法原理及步驟

聚類分析方法是由傳統的分析方法拓展出來，是按照特定要求對事物進行分類的數學方法。實際生活中，要解決的問題往往具有模糊性。一個事物是否屬于某一類、一組事物是否能并為一類等問題不是那么涇渭分明的，不能明確回答 “是”或“否”，這是一個隸屬程度的問題，即只能做出 “某種程度上是或不是”的回答，這就是模糊聚類分析。

模糊聚類是采用模糊數學方法，依據客觀事物間的特征、親疏程度和相似性，通過建立模糊相似關系對客觀事物進行分類的一門多元技術。本文運用模糊聚類分析法對某一行政區路網規劃中的交通小區初步方案進行合并，以期得到更合理的交通小區劃分結果。

模糊聚類分析法的計算過程如下：

STEP1：指標選擇

本文選擇經濟社會和交通運輸方面以下指標作為交通小區劃分的決定因素：人均收入、容積率、地塊面積、產業結構系數、路網面積密度、百人機動車保有量。

STEP2：數據標準化

首先對原始數據進行標準化處理，設域U=｛u1,u2,u3,u4,u5,u6｝為被分類的對象，其中，u1,u2,u3,u4,u5,u6分別表示人均收入、容積率、地塊面積、產業結構系數、路網面積密度、百人機動車保有量。由于原始數據不在［0,1 ］區間，故需對其進行標準化計算。

標準化計算公式為：

將各種標準化值進行數值歸一化，使其轉化到［0,1 ］內。公式為：

STEP3：建立模糊相似矩陣R

rij——各交通小區之間相似系數，得到模糊相似矩陣為：

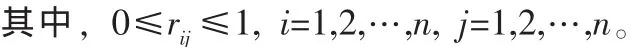
STEP4：模糊等價矩陣

由標定所得到的矩陣R一般為相似矩陣，不滿足傳遞性，故本文采用平方自合成法，將R轉換為模糊等價矩陣Rt。具體做法為建立相似性關系R的傳遞閉包，做成合成運算。

當存在一個數k，使得R2k=Rk·Rk時，停止計算。令Rt=Rk。

STEP5：模糊聚類

設定不同的置信水平λ∈［0,1 ］，對模糊等價矩陣Rt進行聚類處理。若Rt中的元素Cij≥λ，則將集合X中的ui和uj歸為一類，從而得到一系列分類結果。

5 實例分析

現以某市一個行政區為例。初步方案將該區分為8個交通小區。各交通小區的指標值見表1。

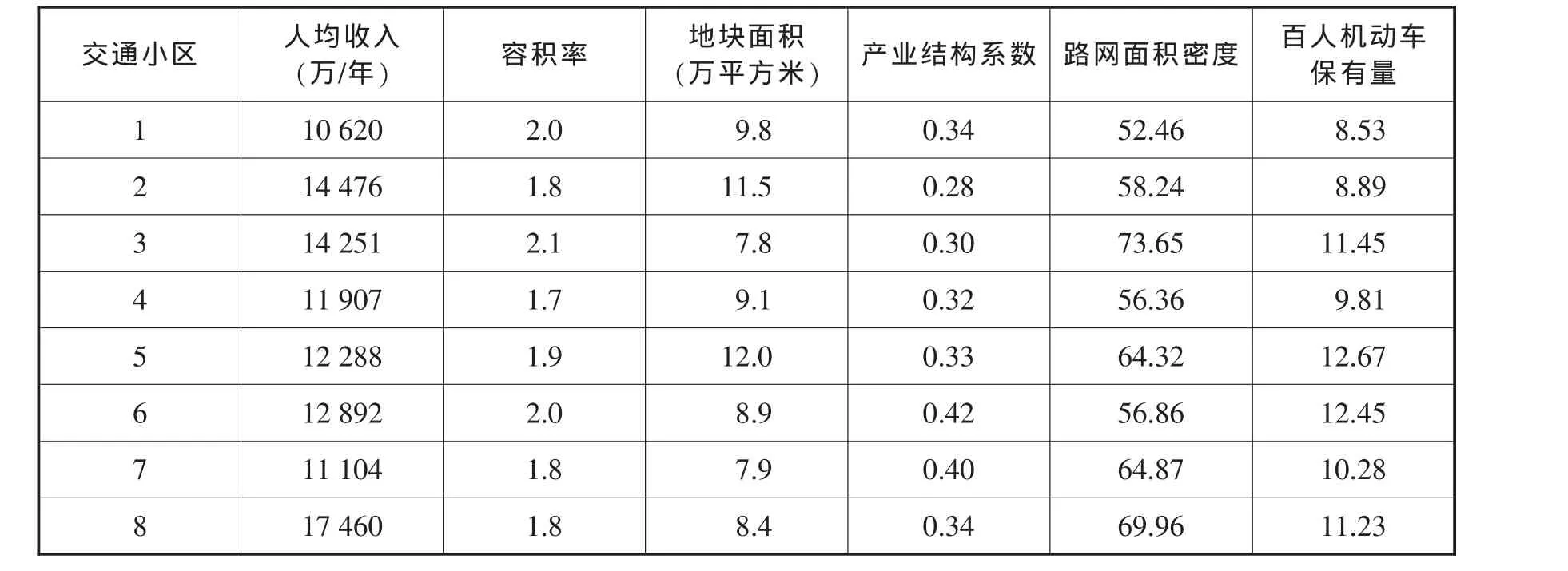
表1

運用MATLAB軟件求得模糊等價矩陣，如表2所示。

表2

不同置信水平λ，得到分類效果如表3。

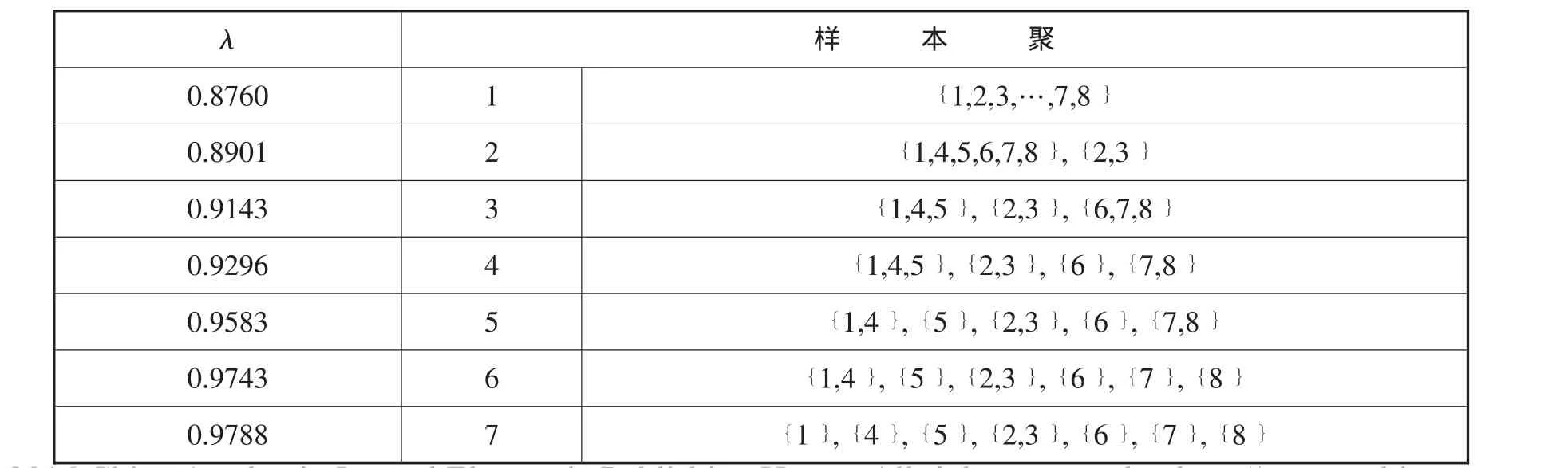
表3

確定最佳閾值λ，取?=0.005，每種分類對應的F統計量如表4。

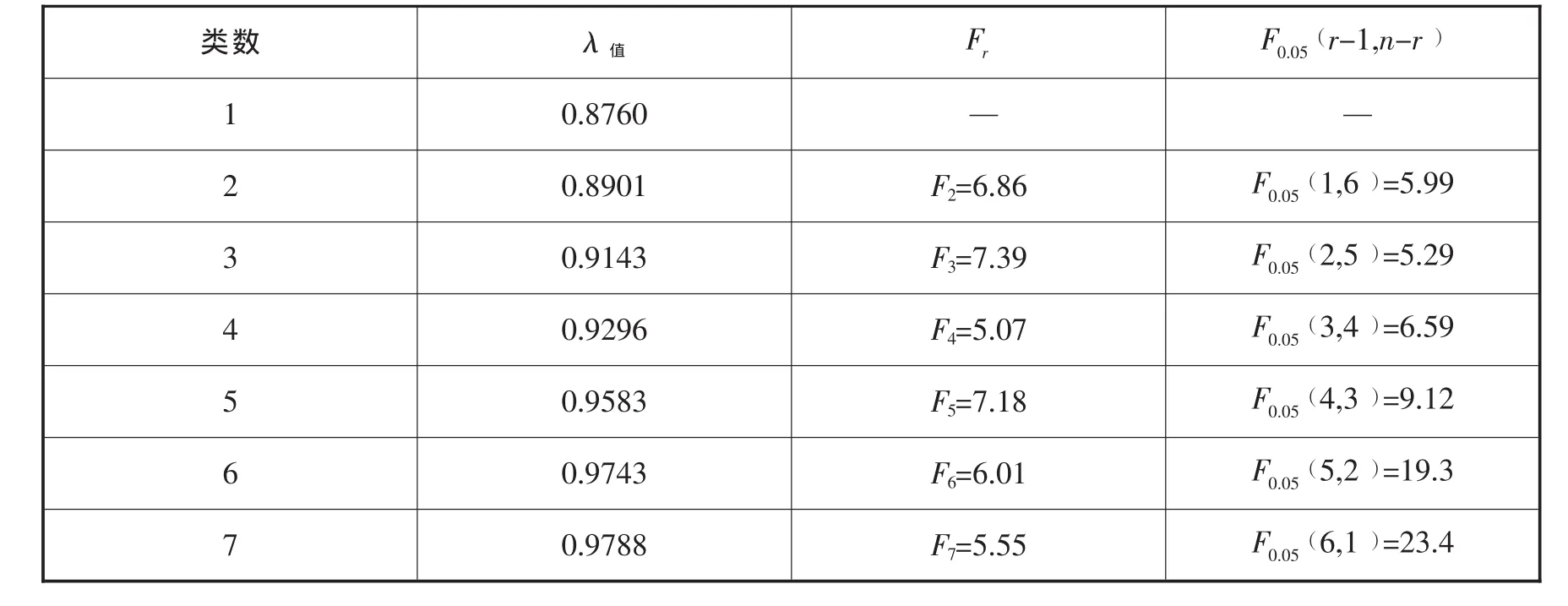
表4

由表4可知， 當 λ=0.8901和 λ=0.9143時，Fr>F0.05（r-1,n-r）。 且F2-F0.05（1,6）=1.07，F3-F0.05（2,5 ）=1.60。 最佳閾值為 λ=0.9143。 把原樣本分為3類。 ｛1,4,5｝,｛2,3｝,｛6,7,8 ｝。

6 總 結

交通小區劃分是進行解析復雜城市交通網絡的有力工具。運用模糊聚類方法對交通小區進行重新分類，為進一步規劃工作提供了前提條件。

[1]高新坡.模糊聚類分析及作用[M].西安：西安電子科技大學出版社，2004.

[2]謝季堅，劉承平.模糊的數學方法的應用[M].武漢：華中科技大學出版社，2005.

[3]王瑞.城市居民出行調查若干問題研究[D].西安：長安大學 （碩士學位論文），2006.

Traffic District Division Method and Application Based on Fuzzy Cluster Analysis

LIU Yi-fei(Shanghai Maritime University Economics and Management School,Shanghai 200135,China)

This paper describes the definition of traffic zones,by the purpose and principles of traffic zone,based on fuzzy cluster analysis,using MATLAB software for clustering analysis,integration solutions.

traffic zones;fuzzy cluster analysis;MATLAB

F570

A

1002-3100(2011)09-0025-04

2011-06-01

上海海事大學研究生創新項目，項目編號：yc2010015。

劉乙霏（1988-），女（壯族），山東臨沂人，上海海事大學經濟管理學院碩士研究生，研究方向：交通運輸規劃與管理。