高壓輸電塔線體系覆冰的研究現狀與展望

劉春城，劉法棟，毛緒坤，李霞輝

(東北電力大學建筑工程學院，吉林吉林132012)

覆冰作為一種特殊的氣象條件，曾給世界各地許多架空線路的安全運行造成嚴重影響。輸電線路所處的環境復雜，低溫、凍雨、濕雪、冰凍等天氣會造成輸電線路嚴重覆冰，引起覆冰閃絡、斷線、倒塔等電網災害，導致供電線路癱瘓，給社會造成了巨大的經濟損失［1-6］。

高壓輸電塔線體系由于在結構上日益趨于桿塔結構高聳、導線截面粗大、跨距長、高差較大等特點，覆冰對其影響更加嚴重;同時，高壓輸電線路的電壓等級較高、載流量較大，線路破壞造成的經濟損失巨大。有必要結合國內外輸電塔線體系的理論研究和工程背景，展開系統的理論研究得到輸電線路覆冰荷載引起的輸電桿塔的破壞機理，協助有關部門完善架空輸電線路的設計規范和確定加固方案，使輸電線路具備抵抗大規模冰雪載荷的能力，從而保障在惡劣環境下電網的安全運行。

1 覆冰機理與類型

導線覆冰首先是由氣象條件決定的，是受溫度、濕度、冷暖空氣對流、環流以及風等因素決定的綜合物理現象。這些因素的不同組合確定了導線覆冰的形狀、密度及厚度。而輸電線路產生覆冰的必要氣象條件是:①具有足可凍結的氣溫，即0℃以下;②空氣中具有過冷卻水滴或云霧;③空氣相對濕度在85﹪以上;④具有可使空氣中的過冷卻水滴或過冷卻云粒產生運動的相應風速，即:風速＞1 m/s［1］。另外，線路的海拔高度、導線懸掛高度以及覆冰發生的凝結高度，也會對線路覆冰產生影響。不同條件的組合將在導線上形成不同類型的覆冰。

通常根據電力系統運行、維護及設計要求，輸電鐵塔和導線的覆冰可以分成以下幾類［7］:

雨凇，一般是由水滴直徑較大的過冷卻雨或毛毛雨在導線的迎風面形成的清澈光滑透明的覆冰，是在凍雨期發生于低海拔地區的覆冰。持續時間一般較短，堅硬，粘附力很強，冰的密度很高，約為0.9～0.92 g/cm3，因其密度大，產生的機械負荷也最大。雨凇覆冰是混合凇覆冰的初級階段，輸電塔和輸電導線覆冰為純粹的雨凇覆冰的情況相對較少［8］。

混合凇，通常是過冷卻水滴在導線的迎風面形成的雨淞與霧淞交替混合凍結形成的不透明或半透明覆冰。形成時間較長，堅硬，粘附力強。混合凇的密度較高，約為0.6～0.9 g/cm3，混合凇生長速度較快，對輸電塔和輸電導線危害特別嚴重［9］。

霧凇，是由于山區低層云中含有的過冷水滴，在溫度極低和風速較小的情況下形成的放射狀的結晶。密度小于0.60 g/cm3，粘附力很弱，對輸電塔和輸電導線一般不構成威脅。

白霜［10］，是空氣中的濕氣與0℃以下的冷物體接觸時，濕氣在冷物表面凝結形成的。白霜粘附力弱，密度為0.05～0.3 g/cm3。對導線威脅不大，但會增加輸電線路的電暈損失。

雪和霧，是由自然降雪粘附在輸電線路上經過多次融化和凍結，成為雪和冰的混合物。有干、濕雪之分，可以達到相當高的質量和體積。

按覆冰的形成機理及形成過程，導線覆冰增長過程可分為兩種:干增長和濕增長［11-13］。導線覆冰后的冰表面水滴部分凍結的覆冰過程稱為濕增長覆冰，濕增長過程一般有冰凌形成;導線覆冰后的冰表面水滴完全凍結的覆冰過程為干增長覆冰，干增長覆冰密度小于純冰的密度，一般無冰凌形成。一般來說，雨淞和濕雪是濕增長過程;而霧淞和干雪是干增長過程;混合凇則是干、濕增長交替進行的過程。但實際上，覆冰過程中條件是不斷變化的，大多數情況下導線覆冰為混合凇。我國北方冬季氣候干燥，輸電線路上主要為積雪;而南方冬季低溫天氣時多產生凍雨，雨淞在輸電線路上易形成密度較大且不宜脫落的覆冰。

2 覆冰預測模型研究

以有關氣象數據為依據，通過理論模型來預測雨淞覆冰荷載的研究工作已進行50多年。期間，提出了許多使用氣象數據的導線雨淞霧淞覆冰計算公式和模型，對覆冰預測模型的研究已由簡單模型發展到復雜模型及雨凇霧凇混合凍結的數值計算模型，一些模型實現導線覆冰的預測已有相當的精度。

Imai［14］認為覆冰強度由導線表面的傳熱控制，是濕增長過程。單位時間單位長度上的雨淞量與空氣溫度(-T)成正比，而與降水強度無關。

式中:C1、C2為常數;V為風速;R為覆冰后的導線半徑;T為氣溫;t為覆冰時間。

這個簡單模型在概念上是正確的，但是覆冰表面的熱量傳遞受到表面粗糙度及蒸發冷卻的影響很難準確確定。在氣溫低于 -5℃ 時會高估導線覆冰量，而在氣溫接近0℃ 時會低估覆冰量，在極端情況下將低估覆冰量。

Lenhard［15］提出了一個最簡單的冰重計算式，每米長導線的冰重M為:

式中:Hg為整個覆冰過程中的降水量;C3、C4為常數。

此模型只牽涉到一個降水量的氣象參數，而忽略了風速、氣溫、濕度等對覆冰的影響。此模型的物理意義不清楚，且過于簡單。

Goodwin［16］認為所有撞擊到導線表面的液滴全部凍結，即覆冰為干增長過程，則單位長度導線的覆冰率為:

式中:W為空氣中的液態水含量;Vi為液滴的撞擊速度。

此模型假設導線上的覆冰為均勻圓筒形冰，且導線對水滴的收集系數為1。但模型計算中需要液滴下落速度的準確值很難確定。

Chaine［17］假設覆冰形狀為不均勻的橢圓形，且為干增長過程。當實際覆冰導線截面為非橢圓形時，引入截面形狀修正系數K，則覆冰的當量徑向厚度為:

式中:修正系數K是導線半徑R0及氣溫T的函數，由經驗確定。

此模型不是用風速和液水含量來計算降水量，而是使用了水流量假設，與其他模型的值相差較遠。

Makkonen［18，19］把導線半徑、氣溫、風速、降水率、風吹角度及覆冰時間等作為輸入量，用數值計算方法對這種考慮冰柱生長的覆冰模型進行了分析和計算。Makkonen在分析凍雨覆冰的濕增長過程中發現，導線上未凍結的液體并沒有全部掉落，而是在導線的底部長成冰柱，而其他模型均未考慮覆冰過程中的這一物理特點。盡管此模型中的液態水含量和水滴大小分布參數不易測量，但其試驗效果十分理想。

劉和云［20，21］在分析凍雨降水產生覆冰的物理過程后，提出了當過冷卻水滴的直徑d取為μm單位時，導線上均勻覆冰時的厚度ΔR可表示為:

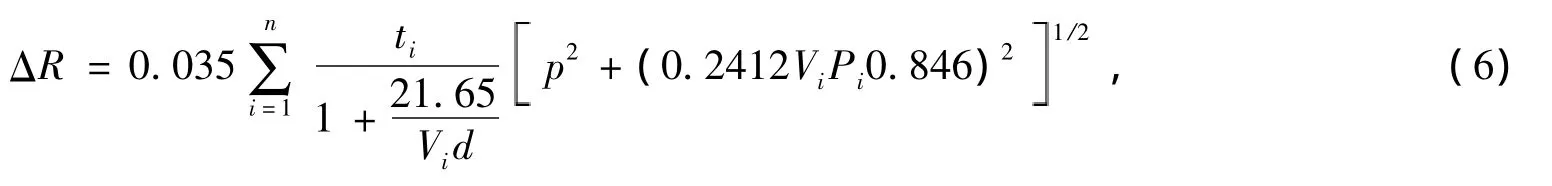
式中:V為風速;P為降水率;N為凍雨的小時數;ti為第i個時間段的長度。

將此模型的預測結果與Imai模型、Lenhard模型、Goodwin模型等復雜模型的預測結果進行了比較，發現此簡單模型取得比較滿意的預測結果。但這些分析都沒有考慮不均勻覆冰和風荷載的影響，有可能高估了輸電塔結構的抗覆冰能力。

這些模型在預測同一氣象條件下產生覆冰的冰重時會出現相差較大的預測結果。因為:①對覆冰時物理模型的細節假設上有差別，如覆冰是干增長還是濕增長過程，均勻覆冰還是非均勻覆冰等;②在經驗數據的選取上不同，如空氣中含濕量與降水率的關系，風速隨高度變化的規律等;③在需要的氣象參數選取上有所區別，如有的模型需要風速、空氣濕度、降水率、空氣溫度等，而有的模型只需要其中的2～3個氣象參數。

3 塔線體系覆冰斷線的理論、模型試驗、數值分析研究

3.1 理論分析

上世紀中期，世界各國研究人員通過不斷努力，在覆冰研究領域取得了許多成果，輸電線路覆冰研究取得了重大進展。

K.F.Jones等［22］在導地線徑向均勻覆冰模型的基礎上，提出了角鋼鐵塔的均勻覆冰數學模型，給出了計算公式，計算了不同截面形狀的一致均勻覆冰厚度。簡單形狀結構上均勻覆冰厚度為t的覆冰面積A(t)為:

式中:t為覆冰厚度;L為角鋼肢長;q、m為形狀參數。

圓柱形結構上均勻覆冰厚度為tc的覆冰面積Ac(tc)為:

式中:l為導線的單位長度;α1、α2、α3分別為水滴在導線表面的碰撞、收集和凍結率。

劉純［6］等對湖南500 kV復沙線倒塔段應用有限元計算程序建立單元模型，計算出鐵塔隨導線覆冰厚度變化的極限承載力，并分析了改事故段鐵塔倒塌的原因。陸佳政等［6，13］對500 kV輸電塔線覆冰進行了有限元分析計算。

H.Max Irvine［24］系統的研究了索結構的靜力和動力特性，就兩端固定索的動力特性進行了分析，采用連續體模型，在考慮纜索剛度與不考慮纜索剛度的情況下對索塔結構進行動力響應分析。該方法精度較高，常用來檢驗離散化模型的計算結果。

李宏男等［25，26］以湖南地區掛靖線220 kV輸電線路覆冰倒塔為例，建立精細化輸電塔線體系有限元模型，依據三峽地區覆冰資料建立覆冰增長曲線，考慮水平垂直檔距、高差、不均勻覆冰和風荷載影響，對覆冰和風荷載作用下輸電塔線體系進行非線性屈曲分析，計算出覆冰荷載以及風荷載與覆冰共同作用下輸電塔結構的極限承載能力，分析了倒塔的主要原因。

S.Ozono等［27］在大量試驗分析的基礎上，提出了求解輸電塔線耦合體系平面動力特性的計算模型，分析了塔線跨數、邊界條件、導線的質量和垂跨比對塔線體系對平面動力特性的影響，探討了塔線耦合對輸電塔和導線振型的影響。

Nigol等［28］初步建立了覆冰導線運動穩定性分析的理論與方法，該理論認為，舞動是由導線自激扭轉引起的。Nigol扭轉舞動理論不僅考慮了偏心覆冰導線在風激勵下的空氣動力特性，還考慮了導線扭轉的影響。

Roshan Fekr等［29］則對檔距為200 m的輸電線路的脫冰過程進行了數值模擬，通過改變單元密度的方法對二十一種典型覆冰及脫冰工況進行了模擬，得出了覆冰厚度和脫冰位置等對輸電線路的影響。

李黎、夏正春等［30］用有限元方法模擬導線斷線和脫冰跳躍對體系的動力響應，建立了導線模型，并以等效彈簧代替導線對輸電塔作用的塔-彈簧模型，將導線在斷線作用下懸垂點的支座反力反向施加在塔-彈簧模型上，數值仿真了輸電塔在導線斷線作用下的動態響應。

侯鐳等［31］針對特高壓線路的脫冰跳躍，計算得到導線脫冰跳躍的時程響應，并分析了脫冰量、檔距組合、導線機械參數、均勻與非均勻脫冰等因素的影響。周迪等［32］用半橢圓霧淞覆冰模型對導線在風力作用下的機械脫冰機理進行了分析研究，獲得了最大剪切力及最大扭轉角的計算方法和公式。

Yasui等［33］為檢驗不同支撐條件下(自立式和拉線式)輸電塔線體系風振響應的差別，將輸電塔簡化為梁或桁架單元，將導線與絕緣子串簡化為桁架單元，在時域內分析了結構的動力響應特性。

從輸電線路的研究進展來看，對覆冰輸電塔線體系方面的研究多是停留在對覆冰輸電導線的單獨研究上，并沒有考慮輸電塔本身和地線的覆冰以及覆冰后塔線之間的耦合作用。對導地線的覆冰只給出了均勻覆冰情況的力學模型，沒有進一步考慮不均勻覆冰的影響，有可能高估了輸電塔線體系的抗覆冰能力。

3.2 模型試驗

高壓輸電塔動力響應的試驗研究是近年來才開展起來的，主要包括風洞試驗和現場實測等研究手段。

Morgan等［34］對一132 kV的五檔輸電線路作了一系列試驗，通過在檔中點釋放固定載荷來模擬脫

式中，tc為覆冰厚度;d為垂直于雨滴軌跡的截面直徑。

蔣興良［1，2，23］等人根據對鄂西及川東地區輸電線路因導線覆冰引起事故的調查結果，分析了三峽地區輸電線路導線覆冰的基本特征，并從理論上建立了導線的霧凇覆冰模型。單位時間dt內霧凇增加的質量dM可表示為:冰過程，并測出了各檔的跳躍高度。

Stewart［35］通過實驗來說明了覆冰對輸電線路的影響。Jamaleddine等［36］在人工氣候實驗室對一個兩檔的輸電線路的縮小模型做了多種脫冰工況的模擬，通過等效系數的換算可以將試驗結果用到實際的輸電線路中去，而且還對所使用的試驗模型進行了數值模擬，模擬結果和實驗結果吻合。

Loredo-Souza等［37］通過修正模型試驗法，初步解決了風洞試驗中模型設計難以同時滿足相似定律和風洞尺寸要求的問題，在導線氣動阻尼、風向變化效應和平行導線相干系數等方面取得了一些有價值的研究成果。

樓文娟等［38，39］以椒江大跨越直線塔為背景，對輸電塔線體系在靜態風作用下的順風響應和脈動風作用下的橫風向及順風向響應進行了試驗測試，并考慮了風速、風向角等因素的影響，提出了輸電塔架橫風響應的簡化計算方法。

鄧洪洲等［40，41］以江陰輸電塔線體系為背景，在均勻流場和紊流場中分別對單塔和塔線體系進行了不同風速下的風振試驗研究。結果表明，導線對塔架自振頻率影響不大，但塔線體系的阻尼較單塔有顯著提高;單塔和塔線體系在均勻流場和紊流場的風振響應譜各階頻率值的大小隨風速變化不大，但隨著風速的增加，功率譜曲線頻譜成分變得飽滿，體系的非線性影響逐漸加強。

氣象參數對電力線路覆冰雪有著決定性的影響，日本在一個風洞設施開展試驗研究［42］，監測單位時間內圍繞導線的雪花分布、風速、濕度、溫度、雪花中的液態水含量、單位長度導線積雪分量、導線旋轉角度、試驗持續時間以及運行導線表面溫度等參量，并分析了各種氣象參數對冰雪的影響。

李宏男等［43，44］根據某輸電塔現場觀測數據，采用模態識別技術對輸電塔和輸電塔線體系的動力響應特性進行了反演，并與數值分析的結果進行了對比，從而驗證了數值方法的正確性;采用數據統計分析與理論模擬的方法分別計算陣風響應因子，并對陣風響應因子的敏感性影響因素進行了識別與分析。研究表明:輸電塔的準靜態陣風因子法是結構設計分析的有效方法，具有較好的計算精度。

王肇民等［46］對塔架的靜力性能和動力性能都進行了大量的開拓性的研究工作，并考慮了桿件初始缺陷及幾何和材料非線性，取得了許多成果。

還有一些學者也應用有限元原理開發了一些輸電塔結構分析軟件，如東北電力設計院在1985年開發了《多塔高、多接腿送電塔滿應力設計軟件》;原電力部的電力建設研究院等單位對輸電塔架進行了不少仿真試驗研究，得到了許多數據資料和有益結論。

4 存在的問題及展望

(1)目前有關覆冰的研究仍存在很多困難:例如對水的物理特性、雪的快速變態、積雪機制的多樣化等因素的研究只能在實驗室進行，人工實驗結果并不理想。有必要設計新方法進行自然積冰雪的研究，積累現場數據，分析覆冰和氣象參數之間的關系。

(2)關于覆冰模型的研究。盡管國內外提出了幾種雨凇覆冰模型，如劉和云建立的簡單模型，雖然比較全面的考慮了各種氣象參數的影響，但是其模型沒有考慮非均勻覆冰的情況，因此需要對該模型進行修正;沒有按不同地區的氣象條件給出模型的確切公式;對于檔內及相鄰檔沿導地線方向的不均勻覆冰缺乏研究。

(3)目前國內外缺少關于輸電塔覆冰模型的研究，輸電塔覆冰后彈性模量、剛度等參數會發生變化，和只考慮導地線覆冰，不考慮輸電塔覆冰的情況有較大差別。此外，研究塔線體系覆冰斷線時，應考慮塔線體系的耦合作用，以及如何計算其耦合影響。

(4)目前國內外關于導地線斷線的研究只是針對覆冰時的風荷載、覆冰舞動、脫冰跳躍等情況分別研究，沒有考慮到這些因素之間的組合對斷線的影響。

(5)關于高壓輸電塔線體系覆冰斷線的現場實測和模型實驗研究以及覆冰斷線造成輸電塔倒塔的動態全過程數值模擬還有待完善。

［1］蔣興良，易輝.輸電線路覆冰及防護［M］.北京:中國電力出版社，2002.

［2］苑吉河，蔣興良，易輝，等.輸電線路導線覆冰的國內外研究現狀［J］.高電壓技術，2004，30(1):6-9.

［3］楊靖波，李正，楊風利，等.2008年電網冰災覆冰及倒塔特征分析［J］.電網與水力發電進展，2008，24(4):4-8.

［4］胡毅，胡建勛，劉庭.我國南方地區電網大范圍覆冰災害的特點分析與防治措施［J］.電力設備，2008，9(6):1-4.

［5］胡毅.電網大面積冰災分析及對策討論［J］.高電壓技術，2008，34(2):215-219.

［6］劉純，陸佳政，陳紅冬.湖南500kV輸電線路覆冰倒塔原因分析［J］.湖南電力，2005，25(5):1-3.

［7］Daisuke Kuroiwa.Icing and Snow Accretion［M］.Monograph series of the research institute of applied electricity，1958.

［8］Makkonen L.Atmosphric Icing on Structure［J］.U S Army CRREL Monograph，1984，84(2):102 - 105.

［9］Macklin W C.The Density and Structure of Ice Formed by Accretion［J］.Quart J Roy Meteor Soc，1962(8):30 -50.

［10］Lahti K，Lahtinen M.Transmission Line Corona Losses under Hoar Frost Conditions［J］.IEEE Trans on Power Delivery，1997，12(2):928 -933.

［11］蔣興良，馬俊，王少華，等.輸電線路冰害事故及原因分析［J］.中國電力，2005，38(11):27-30.

［12］蔣興良.輸電線路導線覆冰機理和三峽地區覆冰規律及影響因素研究［D］.重慶:重慶大學，1997.

［13］陸佳政，蔣正龍，雷紅才，等.湖南電網2008年冰災事故分析［J］.電力系統自動化，2008，32(11):16-19.

［14］Imail.Studies on ice accretion［J］.Researches on Snow and Ice，1953，3(1):35 -44.

［15］lenhard R W.An indirect method for estimating the weight of glaze on wires［J］.Bull.Amer.Meteor.Soc，1955，36(3):1 - 5.

［16］Goodwin E J，etal.Predicting ice and snow loads for transmission lines.Proceedings［C］.First IWAIS，1983:267 -273.

［17］Chaine P M，Casfonguay G.New approach to radial ice thickness concept applied to bundle like conductors［R］.Industrial Meteorology study IV，Environment Canada，Toronto，1974，11.

［18］Makkonen L.Estimating intensity of atmospheric ice accretion on stationary structure［J］.Journal of Appliced Meteorology，1981，20(5):595-600.

［19］Makkonen L.Modeling power line icing in freezing precipitation［C］.7th International Workshopon Atmospheric Icing of Structures，1996，Canada.195 -200.

［20］劉和云.架空導線覆冰防冰的理論與應用［M］.北京:中國鐵道出版社，2001.

［21］劉和云，周迪，付俊萍，等.導線雨凇覆冰預測簡單模型的研究［J］.中國電機工程學報，2001，21(4):44-47.

［22］K.F.Jones，A.B.Peabody.The application of a uniform radial ice thickness to structural sections［J］.Cold Regions Science and Technology，2006，44(2):145 -148.

［23］孫才新，蔣興良，熊啟新，等.導線覆冰及其干濕增長臨界條件分析［J］.中國電機工程學報，2003，23(3):0141-0145.

［24］Irvine H.M.Cable Struetures［M］.Cambridge:MIT Press，1981.

［25］李宏男，白海峰.高壓輸電塔線體系抗災研究的現狀及發展趨勢［J］.土木工程學報，2007，40(2):39-46.

［26］李雪，李宏男，黃連壯.高壓輸電線路覆冰倒塔非線性屈曲分析［J］.振動與沖擊，2009，28(5):111-114.

［27］Ozono S.and Maeda J.In Plane Dynamic interaction between a tower and conductors at lower frequencies［J］.Eng.Structures，1992，14(4):210-216.

［28］O.Nigol，P.G.Buchan.Conductor Galloping.1.Den Hartog Mechanism［J］.IEEE Transactions on Power Apparatus and Systems，1981，100(2):699-707.

［29］M.Roshan Fekr.G.McClure.Numerical modeling of the dynamic response of ice - shedding on electric transmission lines［J］.Atmosphericc Research，1998，46(1/2):1 -11.

［30］李黎，夏正春，等.輸電塔在線路斷線作用下的動力響應［J］.振動與沖擊，2007，26(11):45-49.

［31］侯鐳，王黎明，朱普軒，等.特高壓線路覆冰脫落跳躍的動力計算［J］.中國電機工程學報，2008，28(6):1-6.

［32］周迪，素逸.覆冰導線風動脫冰研究［J］.長沙電力學院學報(自然科學版)，2002，17(2):54-56.

［33］Yasui H，Marukawa H，Momomura Y，Ohkuma Y.Analytical study on wind - induced vibration of power transmission towers［J］.Journal of Wind -Engineering and Industrial Aero - dynamics，1999，83(1):431 -441.

［34］V.T.Morgan.D.A.Swift.Jump height of overhead - line conductors after the sudden release of ice loads［J］.Proceedings IEE 1964，111(10):1736-1746.

［35］J.R.Stewart.Ice as an influence on compact line phase spacing［J］.Proceedings of IWAIS，Hanover，Mew Hampshire，1983:77 -82.

［36］G.McClure.J.Rousselet.R.Beauchenmin.Simulation of Ice - shedding on electrical transmission lines using ADINA［J］.Computers and Structures，1993，47(4/5):523 -536.

［37］Loredo - Souza A M，Davenport A G.A novel approach for wind tunnel modeling of transmission lines［J］.Wind Eng.Ind.Aerodyn，2001，89(11/12):1017-1029.

［38］樓文娟，孫炳楠.風與結構的耦合作用及風振響應分析［J］.工程力學，2000，17(5):16-22.

［39］樓文娟，孫炳楠，唐錦春.高聳格構式結構風振數值分析及風洞試驗［J］.振動工程學報，1996，9(3):108-112.

［40］鄧洪洲，朱松曄，王肇民.大跨越輸電塔線體系動力特性及風振響應［J］.建筑結構，2004，34(7)，25-28.

［41］鄧洪洲，朱松嘩，陳曉明，等.大跨越輸電塔線體系氣彈模型風洞試驗［J］.同濟大學學報，2003，31(2):132-137.

［42］Sakamoto Y.Snow accretion on overhead wires［J］.Philosophical Transactions of the Royal Society，2000，358(1776):2941 -2970.

［43］李宏男，石文龍，賈連光.導線對輸電塔體系縱向振動的影響界限及簡化抗震計算方法［J］.振動與沖擊，2004，23(2)1-7.

［44］李宏男，任月明，白海峰.輸電塔體系風雨激勵的動力分析模型［J］.中國電機工程學，2007，27(30):43-48.

［45］王肇民.桅桿結構［M］.北京:科學出版社，2000.