面向齒輪箱故障診斷的序貫概率比檢驗(yàn)理論和方法
尚云飛,陳漢新,孫 魁
(武漢工程大學(xué)機(jī)電工程學(xué)院,湖北 武漢,430205)
0 引 言
1947年,Wald[1]提出了序貫概率比檢驗(yàn)算法.該算法基于兩種假設(shè):(1)樣本要滿足獨(dú)立同分布;(2)樣本的先驗(yàn)分布要已知,如滿足正態(tài)分布等[2].序貫概率比檢驗(yàn)算法應(yīng)用于齒輪箱的故障診斷與傳統(tǒng)的故障診斷方法不同的是,不需要預(yù)先設(shè)定檢驗(yàn)樣本的數(shù)量,而是將序貫概率比檢驗(yàn)后的值與預(yù)先設(shè)定的閾值進(jìn)行比較,從而判斷設(shè)備的運(yùn)行狀態(tài)[3].
在齒輪故障診斷實(shí)驗(yàn)中,選用齒輪裂紋來模擬齒輪故障.實(shí)驗(yàn)中得到的信號(hào)會(huì)夾雜著噪聲等干擾,影響了信號(hào)的穩(wěn)定性.首先,采用小波包降噪的方法對(duì)信號(hào)進(jìn)行預(yù)處理,以得到穩(wěn)定的振動(dòng)信號(hào).再運(yùn)用時(shí)域分析法提取信號(hào)的特征值,最后對(duì)信號(hào)進(jìn)行序貫概率比檢驗(yàn).為了驗(yàn)證序貫概率比檢驗(yàn)算法用于齒輪箱故障診斷的診斷能力,選用均方根誤差的方法來驗(yàn)證該方法的有效性.
1 序貫概率比檢驗(yàn)原理

對(duì)于一個(gè)二元序貫概率比檢驗(yàn),零假設(shè)和被擇假設(shè)分別表示為H0∶θ=θ0和H1∶θ=θ1.它們的聯(lián)合分布密度函數(shù)為
(1)
其中,j=0,1.序貫概率比檢驗(yàn)的似然比λ為
λn(x)=λn(x1,…,xn)=
(2)
假設(shè)x1是采樣得到的第一個(gè)觀測(cè)數(shù)據(jù)值,將其帶入公式(2)中計(jì)算似然比,記為λ1(x1).按預(yù)先設(shè)定的閾值對(duì)兩種故障模式進(jìn)行識(shí)別.如果似然比滿足λ1(x1)
民營(yíng)企業(yè)從銀行獲得貸款也不容易。“銀行能給我們的貸款額度在收緊。”某文旅企業(yè)負(fù)責(zé)人周珊彤說,“我們找銀行貸款,額度上就會(huì)打折扣,放款也不能一次到位,而是要分幾批發(fā)放,銀行的解釋是上級(jí)行對(duì)規(guī)模管理得較嚴(yán)。”
根據(jù)假設(shè)檢驗(yàn)中犯第一類錯(cuò)誤的概率α與犯第二類錯(cuò)誤的概率β確定閾值A(chǔ)和B(A>B).檢驗(yàn)中的閾值A(chǔ),B與α,β的關(guān)系滿足如下式子:
(3)
(4)
2 齒輪箱故障診斷實(shí)驗(yàn)
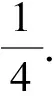
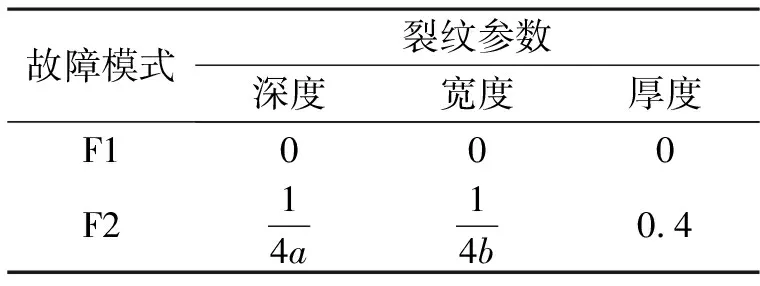
表1 兩種故障模式
如圖1所示的齒輪箱工作結(jié)構(gòu)圖,振動(dòng)是由齒輪3與齒輪4之間的沖擊力產(chǎn)生的,實(shí)驗(yàn)中選取齒輪3來模擬故障模式.
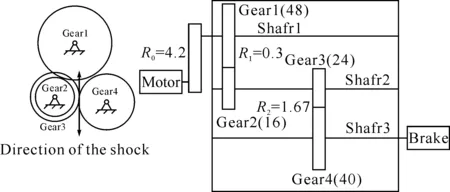
圖1 齒輪箱工作結(jié)構(gòu)圖
將兩個(gè)加速度傳感器分別安裝在齒輪箱的水平和垂直方向,采用動(dòng)態(tài)模擬器來采集齒輪箱振動(dòng)信號(hào).本文只對(duì)安裝在水平方向上的傳感器所測(cè)得的振動(dòng)信號(hào)進(jìn)行分析.將正常狀況下得到的振動(dòng)信號(hào)記為S1,故障狀況下得到的振動(dòng)信號(hào)記為S2.
3 齒輪裂紋的序貫概率比檢驗(yàn)
3.1 小波包降噪
小波包變換通過對(duì)信號(hào)的低頻部分和高頻部分的同時(shí)分解來提高時(shí)頻分辨率.將實(shí)驗(yàn)信號(hào)進(jìn)行3層小波包分解,就可以得到8個(gè)正交頻帶的振動(dòng)信號(hào),再對(duì)信號(hào)進(jìn)行重構(gòu)[4].這可以對(duì)信號(hào)處理得更細(xì)致、準(zhǔn)確.得到適合序貫概率比檢驗(yàn)的平穩(wěn)信號(hào).
3.2 特征參數(shù)提取
特征參數(shù)可以反映振動(dòng)信號(hào)的特征信息,從原始振動(dòng)信號(hào)中提取相關(guān)的特征參數(shù),將其預(yù)處理后作為序貫概率比檢驗(yàn)的檢驗(yàn)參數(shù)[5-8].實(shí)驗(yàn)中的離散待檢信號(hào)xi=[x1,x2,…,xN],N=8 192,每組取1 024個(gè)檢驗(yàn)點(diǎn),這樣就可以得到7 169組檢驗(yàn)數(shù)據(jù).幾個(gè)特征參數(shù)按下面公式計(jì)算:
均值:
(5)
峭度值:
(6)
峭度值的所有取值作為作為序貫概率比檢驗(yàn)的檢驗(yàn)參數(shù),表示為ki=[k1,…,kn],其均值和標(biāo)準(zhǔn)差為:
均值:
(7)
標(biāo)準(zhǔn)差:
(8)
3.3 齒輪裂紋的序貫概率比檢驗(yàn)
由序貫概率比檢驗(yàn)的基本原理可知,待檢驗(yàn)序列的均值和方差對(duì)似然比有較大的影響.經(jīng)過預(yù)處理后,幾組檢驗(yàn)參數(shù)的序列基本滿足高斯分布.在正常狀況下,該信號(hào)序列滿足零假設(shè)H0∶μ=μ0;在故障狀況下,該信號(hào)序列滿足被擇假設(shè)H1∶μ=μ1.標(biāo)準(zhǔn)差σ不變,均值變化,在零假設(shè)和備擇假設(shè)均成立的條件下,該序列的聯(lián)合概率密度分別表示為:
(9)
(10)
式(10)中,p0i和p1i分別為零假設(shè)和備擇假設(shè)條件下的概率密度函數(shù).序貫概率比檢驗(yàn)的似然比為
(11)
式(11)中,P0和P1分別為零假設(shè)和備擇假設(shè)條件下的先驗(yàn)概率.
在實(shí)際應(yīng)用中,為了計(jì)算方便且準(zhǔn)確,公式(11)可以轉(zhuǎn)化為下面形式[9]:
(12)
此時(shí),閾值a=lnA,b=lnB.
如果似然比滿足Δ 圖2 齒輪箱序貫概率比檢驗(yàn)流程圖 為了檢驗(yàn)采用序貫概率比檢驗(yàn)算法對(duì)齒輪裂紋進(jìn)行故障診斷的診斷性能和可行性,用均方根誤差算法來評(píng)估其診斷能力.均方根誤差定義為: (13) 對(duì)于正常狀況和故障狀況兩種故障模式,實(shí)驗(yàn)中共得到圖3所示的S1和S2兩組振動(dòng)信號(hào). 圖3 兩組實(shí)驗(yàn)振動(dòng)信號(hào):(S1)為正常狀況;(S2)為故障狀況 對(duì)實(shí)驗(yàn)信號(hào)進(jìn)行小波包去噪處理,得到穩(wěn)定的信號(hào),如圖4所示. 圖4 小波包去噪后的振動(dòng)信號(hào),(S1)為正常狀況;(S2)為故障狀況 峭度值對(duì)沖擊性特性很敏感,均值偏差對(duì)似然比、檢驗(yàn)時(shí)間的長(zhǎng)短以及檢驗(yàn)的準(zhǔn)確性都有影響.對(duì)假設(shè)H0和H1,規(guī)定犯第一類錯(cuò)誤的概率與犯第二類錯(cuò)誤的概率相等,取α=β=0.005,并且所觀測(cè)信號(hào)的先驗(yàn)概率是相等的. 由序貫概率比檢驗(yàn)的基本原理可知,均值變化量對(duì)似然比Δ的影響較大.以正常狀況下的信號(hào)S1的均值作為參數(shù)μ0,以故障狀態(tài)下的信號(hào)S2的均值作為參數(shù)μ1,對(duì)信號(hào)進(jìn)行檢驗(yàn),得到如圖5所示的圖形. 圖5 以正常狀況下的信號(hào)S1的均值作為參數(shù)μ0,以故障狀態(tài)下的信號(hào)S2的均值作為參數(shù)μ1的序貫概率比檢驗(yàn)結(jié)果 當(dāng)以正常狀況下的信號(hào)S1的均值作為參數(shù)μ0,以故障狀態(tài)下的信號(hào)S2的均值作為參數(shù)μ1時(shí),分別將信號(hào)S1和S2輸入似然比公式中檢驗(yàn),得到圖5.圖5說明輸入信號(hào)S1時(shí),似然比滿足Δ 實(shí)驗(yàn)中,在正常狀況下獲得兩組實(shí)驗(yàn)數(shù)據(jù),每一組預(yù)處理并提取特征值后得到7 169個(gè)數(shù)據(jù)點(diǎn),兩組信號(hào)就共有14 338個(gè)數(shù)據(jù)點(diǎn).將這些數(shù)據(jù)點(diǎn)分為16小組,分別記為A1,B1,C1,D1,E1,F(xiàn)1,G1,H1,I1,J1,K1,L1,M1,N1,O1,P1組.將每一組數(shù)據(jù)進(jìn)行序貫概率比檢驗(yàn),得到16個(gè)似然比的值,分別記為A2,B2,C2,D2,E2,F(xiàn)2,G2,H2,I2,J2,K2,L2,M2,N2,O2,P2.用均方根誤差方法來計(jì)算這16個(gè)似然比之間的誤差,即A2分別與B2到P2這15個(gè)似然比比較,B2分別與C2到P2這14個(gè)似然比比較,C2分別與D2到P2這13個(gè)似然比比較,…,O2與P2比較,得到15組比值,其中每組比值中的最大值分別如以下圖中所示的m1,m2,m3,…,m15.故障模式下計(jì)算的似然比記為a,運(yùn)用均方根誤差算法分別與上面的16組似然比值比較,即a與A2,B2…P2比較,計(jì)算不同故障模式之間的誤差,共得到到16個(gè)誤差值點(diǎn),形成的誤差曲線如下面圖中的曲線.通過誤差的比較來評(píng)估序貫概率比檢驗(yàn)算法應(yīng)用于齒輪裂紋的故障診斷的診斷能力. 以正常信號(hào)的均值作為參數(shù)μ0,以故障信號(hào)的均值作為參數(shù)μ1,建立序貫概率比檢驗(yàn)?zāi)P?檢驗(yàn)結(jié)果如圖6所示. 將實(shí)驗(yàn)中得到并預(yù)處理后的14 338個(gè)正常齒輪的數(shù)據(jù)信號(hào),分為16組,進(jìn)行序貫概率比檢驗(yàn),得到圖6(a)所示的16條normal曲線.同理,對(duì)故障的數(shù)據(jù)信號(hào)進(jìn)行序貫概率比檢驗(yàn),得到圖6(a)所示的fault曲線.圖6(a)說明16組正常信號(hào)的似然比曲線大體趨勢(shì)相同,與故障信號(hào)的似然比曲線有明顯的差異.運(yùn)用均方根誤差算法計(jì)算16組正常信號(hào)的似然比之間的誤差,共得到15組誤差數(shù)據(jù),每組誤差數(shù)據(jù)中的最大值如圖6(b)中的條形圖所示.繼續(xù)計(jì)算故障信號(hào)分別與正常信號(hào)似然比之間的誤差,得到如圖6(b)所示的誤差曲線.圖6(b)說明不同故障模式之間的誤差遠(yuǎn)大于同種故障模式彼此之間的誤差,也就是說,序貫概率比檢驗(yàn)算法可以對(duì)不同故障模式進(jìn)行有效的分類和識(shí)別. 圖6 16組正常信號(hào)和故障信號(hào)的序貫概率比檢驗(yàn)及誤差計(jì)算 基于序貫概率比檢驗(yàn)算法建立了一種新的齒輪箱故障診斷模型.通過對(duì)正常和故障齒輪狀態(tài)的識(shí)別與檢驗(yàn),來檢驗(yàn)序貫概率比檢驗(yàn)算法的有效性.實(shí)驗(yàn)中得到的振動(dòng)信號(hào)夾雜著噪聲等干擾,采用小波包去噪方法對(duì)原信號(hào)進(jìn)行預(yù)處理,得到穩(wěn)定的檢驗(yàn)信號(hào).采用時(shí)域分析法提取信號(hào)的特征值,本文中提取對(duì)沖擊性振動(dòng)敏感的峭度值作為特征值.運(yùn)用均方根誤差算法來檢驗(yàn)序貫概率比檢驗(yàn)算法的診斷能力.結(jié)果表明本文提出的方法能夠有效地對(duì)齒輪進(jìn)行故障診斷.序貫概率比檢驗(yàn)算法對(duì)齒輪裂紋的識(shí)別和診斷具有很好的有效性和可行性.此外,上述方法也適用于復(fù)雜旋轉(zhuǎn)機(jī)械的故障診斷與檢測(cè). 參考文獻(xiàn): [1]Wald A.Sequential Analysis[M].New York:Wiley,1947. [2]Yu Chenggang,Su Bingjing.A non-parametric sequential rank-sum probability ratio test method for binary hypothesis testing[J].Signal Processing,2004(84):1267-1272. [3]李煒,朱蕓,毛海杰,等.SPRT檢驗(yàn)法和小波變換法在管道泄漏檢測(cè)中的應(yīng)用[J].計(jì)算機(jī)測(cè)量與控制,2005(9):903-904. [4]舒苗淼,劉廣璞,潘宏俠.基于小波包分解的機(jī)械振動(dòng)信號(hào)分析[J].起重運(yùn)輸機(jī)械,2009(9):61-64. [5]魯艷軍,陳漢新,賀文杰,等.基于混合特征提取和WNN的齒輪箱故障診斷[J].武漢工程大學(xué)學(xué)報(bào),2011,33(5):82-88. [6]陳漢新,王慶軍,陳緒兵,等.基于解調(diào)振動(dòng)信號(hào)特征提取齒輪箱的故障診斷[J].武漢工程大學(xué)學(xué)報(bào),2010,32(9):67-77. [7]賀文杰,Bajolet Julien,Yoann Plassard,等.基于EMD和FFT的齒輪箱故障診斷[J].武漢工程大學(xué)學(xué)報(bào),2011,33(1):65-70. [8]安妮,徐建民.齒輪箱振動(dòng)的故障診斷與實(shí)例分析[J].武漢工程大學(xué)學(xué)報(bào),2011,33(12):70-72. [9]Min Z H,Sun L M.A novel non-parametric sequential probability ratio test method for structural condition assessment[C]∥Health Monitoring of Structural and Biological Systems.Edited by Kundu,Tribikram,Proceedings of the SPIE,2010(7650):1-9.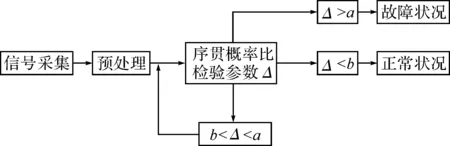
3.4 誤差分析
4 結(jié)果與分析
4.1 實(shí)驗(yàn)結(jié)果
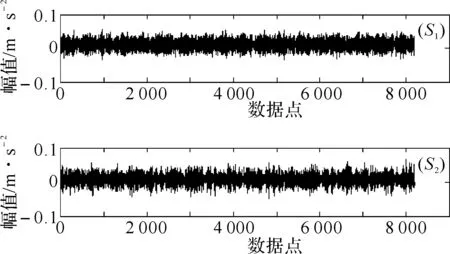
4.2 預(yù)處理結(jié)果
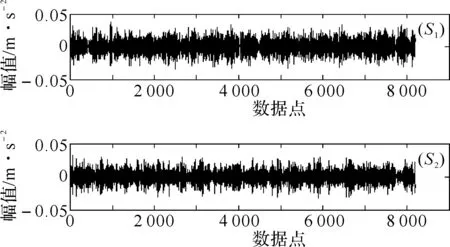
4.3 序貫概率比檢驗(yàn)結(jié)果分析

4.4 誤差結(jié)果分析
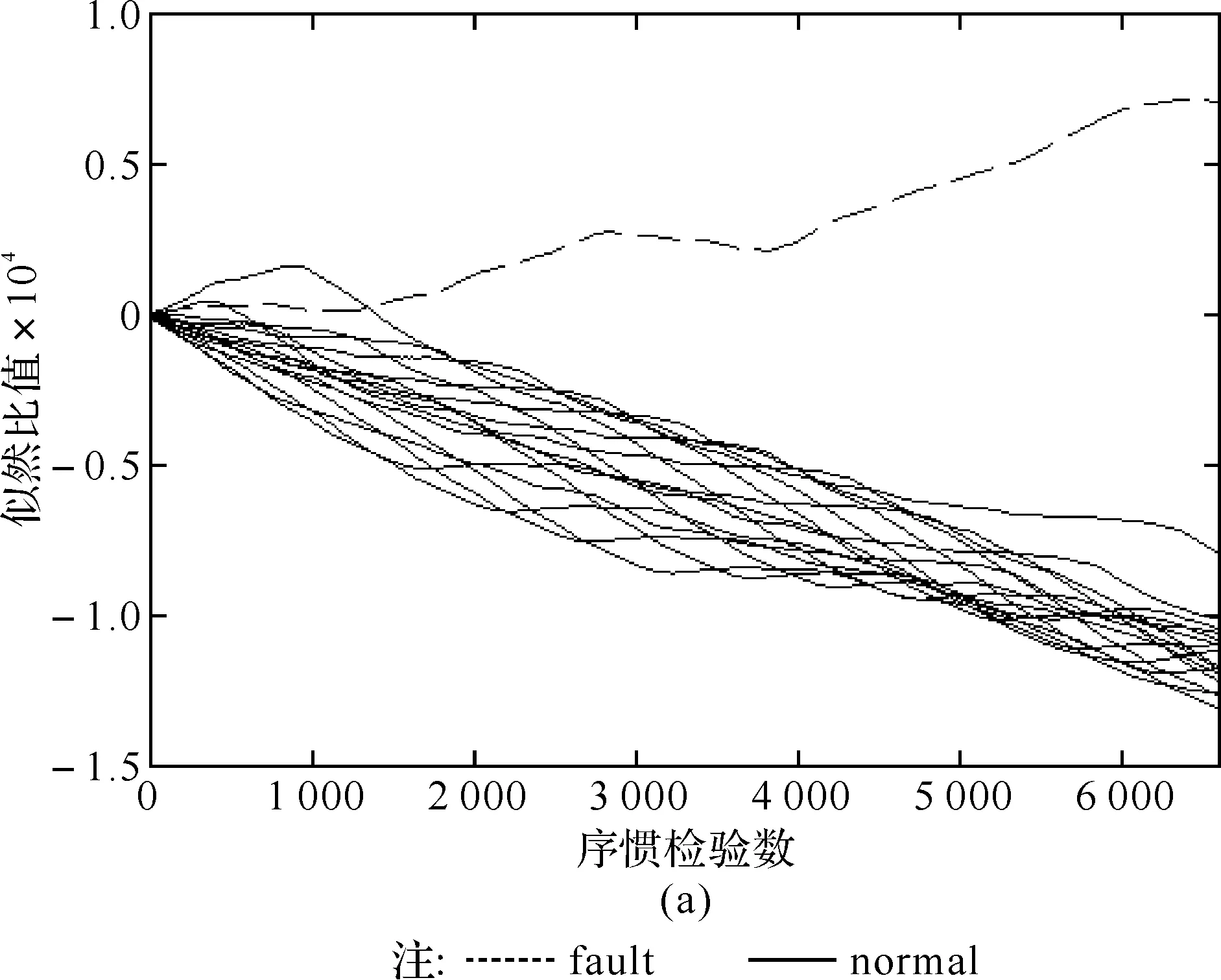
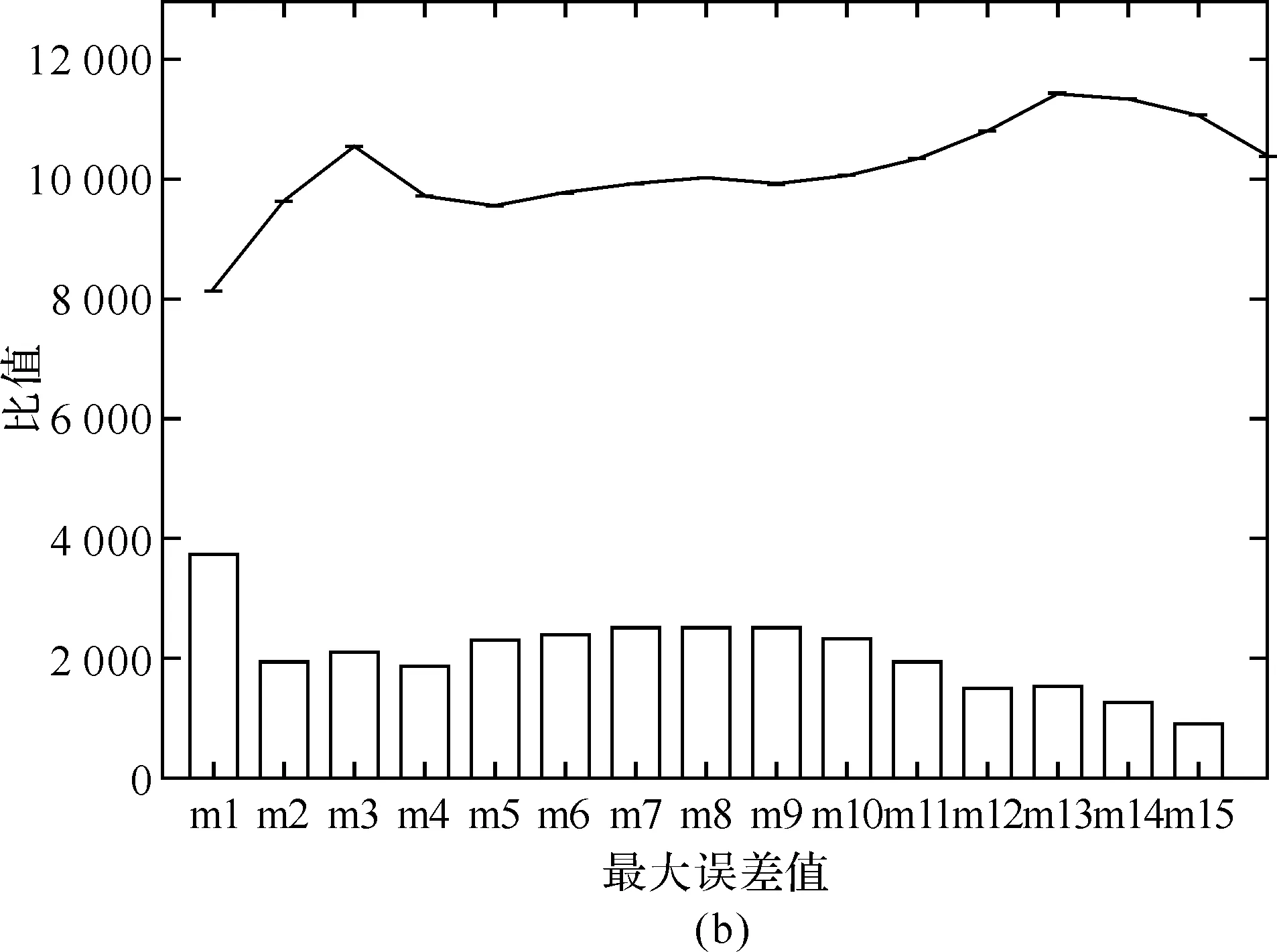
5 結(jié) 語

