電力設備三維網格模型自適應魯棒水印算法

朱少敏 劉建明

（1.中國電力科學研究院 北京 100192 2.國網信息通信有限公司 北京 100761 3.北京市電力公司變電公司 北京 100054）

1 引言

隨著電力企業信息化程度提高和多媒體信息技術廣泛普及，電力生產和管理過程中應用大量圖像、音頻、視頻和三維模型等多媒體信息[1]。保證多媒體信息安全正成為電力信息安全研究與發展中亟待解決的難題之一[2-4]。數字水印技術是解決多媒體信息安全的一種重要且有效的方法[5-7]，在電力數字信號版權保護、可信文檔傳輸、電量交易、數字信號質量評價及分析等方面有著廣泛應用[8-9]。

三維網格模型水印算法按照嵌入領域不同，分為空間域算法和變換域算法。空間域算法通過直接修改網格頂點坐標、拓撲結構或定義特定面積比、體積比及距離值，實現水印嵌入。Ohbuchi等[10]首次提出三維模型兩個水印算法：三角形相似四元組（Triangle Similarity Quadruple，TSQ）算法和四面體體積比（Tetrahedral Volume Ratio，TVR）算法。通過調整網格模型頂點坐標，改變距離比和體積比實現水印嵌入，算法可以抵抗仿射攻擊，但抗噪聲和網格拓撲攻擊較差。文獻[11]通過將三維模型多次映射到兩個約束集中并修改約束集頂點位置嵌入水印，可以抵抗網格連通性攻擊。文獻[12]提出利用模型頂點局部集信息選取恰當的水印嵌入點，通過修改嵌入點頂點坐標嵌入水印信息，算法可以抵抗網格加噪、平滑濾波等攻擊。Yu等[13]通過修改網格頂點到模型質心距離實現水印嵌入，所加水印強度不能太大，容易改變網格模型的視覺保真度。文獻[14]提出利用網格模型具有仿射不變量特性的重心交點距離比（Ratio of Barycenter and Crosspoint，RBC）嵌入水印，利用加速的頂點和重心連線與模型求交的方法，求得連線與模型的交點，計算出重心交點距離比。通過修改一個三角形面片三個頂點對應的RBC嵌入多個水印字符。算法可以抵抗仿射變換、頂點亂序和噪聲攻擊。

變換域算法一般首先對網格模型進行某種變換，在變換域內實現水印嵌入。水印嵌入完后通過反變換得到含水印后的模型。Kanai等[15]基于網格多分辨率分析的思想，將原始三維網格模型進行小波變換，通過修改小波系數嵌入水印信息。Olbuchi等和Cayer等[16-17]提出的算法都是通過利用網格模型拓撲關系建立Laplace矩陣，通過修改偽頻譜系數實現水印嵌入。與空間域算法相比，變換域算法能將水印嵌入到整個網格模型中，通常算法魯棒性高于空間域算法，但相對比較復雜，計算效率不高。

本文首先利用電力設備三維網格模型離散曲率估計，確定網格模型臍點。將選取的模型臍點離散法向量與其局部粗糙度結合起來，自適應地將臍點坐標分別投影到其最大主方向和最小主方向，修改臍點坐標值實現水印嵌入。水印提取過程是嵌入過程的逆過程。在有原始設備模型參與下，準確提取具有版權保護功能的魯棒水印。實驗結果表明，算法不僅具有良好的視覺保真度，而且對多種網格模型處理和攻擊具有較強魯棒性。

2 離散曲率估計和主方向分析

一般來說，曲面的一階微分量是指曲面的切平面方向和法向量，二階微分量是指曲面的曲率等有關量[18]。目前，估算離散曲面微分量方法并不統一。針對三維網格曲面，許多學者紛紛提出各自的離散高斯曲率或離散平均曲率計算方法。Moreton等[19]利用微分幾何歐拉定理，建立曲面法曲率與曲面主曲率及主方向關系。Taubin等[20]利用曲率張量方法，對三角網格中每一點估計一個局部矩陣，通過求解該矩陣特征值和特征向量獲得主曲率和主方向。但是利用這些方法，主曲率方向或曲率張量的估計并不準確和魯棒。為了更準確地估計離散微分量，Cohen-Steiner利用法線環（Normal cycle）理論在給定頂點周圍選取小的鄰域求平均值，實現對曲面上每點曲率張量準確估計，具有良好收斂性[21]。

Cohen-Steiner方法利用頂點測地鄰域的矩陣特征值和特征向量獲得主曲率和主方向[22]。對網格上每個頂點pi，將所有滿足到點pi的測地距離不大于給定距離ri的點，作為頂點pi的測地鄰域B。只考慮鄰域內的點和邊，定義以下矩陣

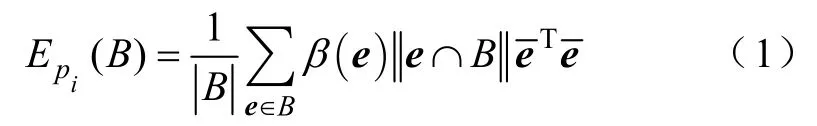
將Epi(B)最小特征值的特征方向作為頂點pi處網格曲面法向量估計式。以最大特征值和最小特征值作為網格頂點主曲率k1,k2估計。法曲率取得最大值的方向k1為最大主方向e1，最小值k2的方向為最小主方向e2。

圖1 點pi測地鄰域B和角度β(e)Fig.1 The neighborhood B and angle β between the normals of the faces adjacent to the edge e

3 自適應魯棒水印算法

3.1 水印嵌入算法

（1）臍點的概念最早源自于微分幾何，將曲面上所有方向的法曲率都相等的點定義為臍點。這些臍點是曲面張量場中的拓撲奇異點，反應了模型內在特征，對常見的網格處理操作具有魯棒性，是網格模型特征點[23]。利用臍點可以較好地對網格模型進行形狀分析和特征提取，因此本文選取電力設備三維網格模型的臍點作為水印嵌入點。水印嵌入過程如圖2所示。

（2）生成魯棒水印并加密預處理。采用與網格模型臍點相同個數的隨機實數作為水印，滿足以0為中心l為方差的高斯分布，由模型作者版權信息哈希值組成的密鑰key1作為隨機數生成器種子數，產生水印向量，L為水印長度，其等于網格模型臍點數。為了進一步加強水印安全性，利用Logistic混沌密鑰key2產生的混沌序列異或加密魯棒水印。

（3）以高斯曲率KG和平均曲率KH作為約束條件，計算得到曲率張量的兩個特征向量e1和e2，分別為最大主方向和最小主方向。

（4）借鑒文獻[23]的方法，將通過預處理混沌加密后的魯棒水印自適應沿著最大主方向和最小主方向修改嵌入臍點坐標值，實現魯棒水印嵌入。

式中，ξi為對應嵌入臍點的嵌入強度。

3.2 自適應嵌入強度

在水印嵌入過程中（見圖2），為了保證含水印的三維網格模型失真度降低到最小，同時能夠抵抗一定程度網格攻擊，需要根據網格模型局部幾何特征并結合人眼視覺掩蔽特性，確定水印嵌入強度。但是因為三維網格模型是由離散點面信息組織起來，缺乏統一參數化信息，無法直接將已有的視覺掩蔽特征直接應用到三維領域。本文將網格模型頂點的一維微分估算和二維微分估算結合起來，提出一種基于離散微分估算的視覺掩蔽模型，為水印嵌入頂點加入一個局部強度函數，使水印嵌入強度根據網格局部特征自適應變化，實現自適應水印算法。

根據頂點vi一環鄰居，計算其離散法向量ni

式中，Ni表示與頂點vi相連的頂點個數。

將其每個分量的絕對值作為在此鄰域內的頂點坐標變化的量度，并用它們作為這個頂點水印強度的控制因子[24]，定義頂點vi水印掩蔽因子M1(vi)為

同時，考慮利用網格頂點局部粗糙度作為水印掩蔽因子M2(vi)。模型粗糙度越小，表示模型表面越光滑，水印嵌入強度不能過大；反之，粗糙度越大，則可以嵌入強度更大的水印信息。基于高斯主曲率分割方法，文獻[25]提出一種網格模型局部粗糙度計算方法，定義過程如下：

（1）對原始網格模型進行自適應平滑濾波。

（2）分別計算原始網格模型和平滑后模型的頂點最大曲率。

（3）定義網格模型的局部窗口大小，利用已計算的頂點最大曲率，分別計算原始網格模型和平滑后模型的頂點平均曲率。

（4）利用式（5），確定網格模型頂點vi粗糙度，即

式中，kav(vi) 和kav(vsi) 分別表示原始網格模型和平滑后模型的平均曲率。同時，原始模型中某些陡沿特征中經過平滑后，其kav(vi) 可能不大于kav(vsi)，將這些點的粗糙度置零。

將網格頂點vi一階微分量和二階微分量結合起來，定義如下頂點嵌入強度函數[27]：

式中，M2(mean)和M2(min)分別為網格模型頂點局部粗糙度平均值和最小值；α1,α2為嵌入強度參數。

圖2 水印嵌入過程Fig.2 Watermark embedding process

3.3 水印提取算法

本文水印算法是一種非盲水印算法，在水印提取過程中需要原始電力設備三維網格模型。水印提取過程如圖3所示，提取算法步驟簡介如下：

（1）含水印的電力設備三維網格模型可能會遭受到網格仿射變換或連通性攻擊，這些攻擊會導致網格模型位置關系或拓撲關系發生改變，所以在水印提取前，需要利用原始模型來對待檢測模型進行網格重定位或網格重采樣的預處理。

（2）以Cohen-Steiner方法估算出原始電力設備三維網格模型離散曲率信息，找出原始模型臍點位置，確定水印嵌入位置。

（3）計算原始電力設備網格模型和含水印模型臍點的向量，并對其歸一化處理。

（4）將歸一化后臍點向量qi分別在最大主方向和最小主方向進行投影。通過比較qi在e1和e2方向上投影大小，提取水印信息。

圖3 水印提取過程Fig.3 Watermark extraction process

4 實驗結果與分析

4.1 實驗條件

為了驗證本文所提出的魯棒水印算法性能，以P4 2.4GHz，2G內存計算機為平臺，并以三維激光掃描儀獲得的電力系統中實際應用的電力設備模型為實驗對象，選取常見的避雷針和變壓器兩種三維網格模型，進行實驗。兩種原始電力設備網格模型如圖4所示，模型基本情況見表1。

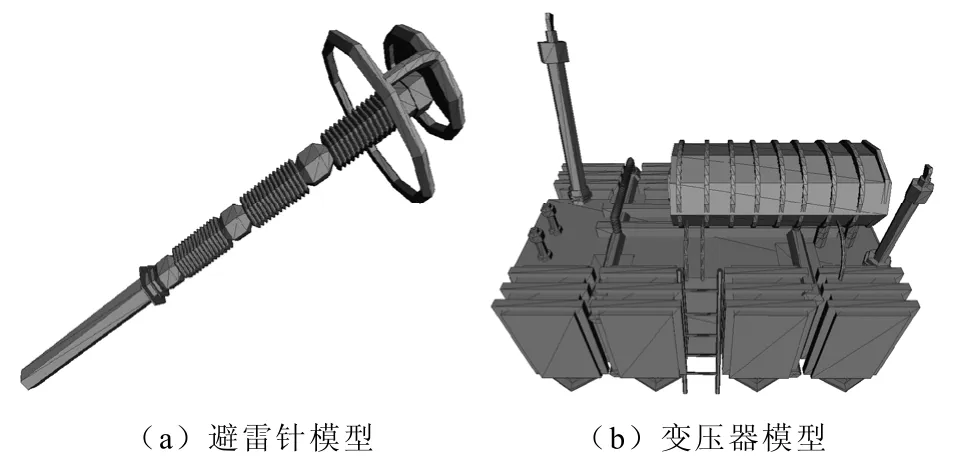
圖4 原始電力設備三維網格模型Fig.4 Original electric power equipment 3D mesh models

表1 電力設備三維網格模型的基本情況Tab.1 Electric power equipment 3D mesh models basic information

4.2 不可見性分析

目前大多數三維模型水印算法的不可見性均是直接通過主觀視覺評測來判讀水印算法的保真度，缺乏對含水印三維模型客觀評價。有的算法采用最大根方均差 (Maximum Root Mean Square Error，MRMS)[26]，信噪比 (Signal Noise Ratio，SNR)[12]等客觀評價方法，但這些評價標準均是基于網格頂點之間的誤差，并不能完全準確反映不同模型之間的視覺差異，這是因為人眼在觀察三維模型時，主要提取的是三維網格模型結構信息，而不是網格模型頂點坐標之間的誤差。與圖像類似，三維網格結構失真才是網格模型質量評價中至關重要的因素。

本文選取網格結構失真度(Mesh Structural Distortion Measure，MSDM)作為網格水印不可見性客觀評價標準。對于待比較的含水印模型和原始模型，文獻[27]通過定義曲率、對比度和結構比較函數，實現對兩個模型結構失真度的客觀度量。設原始模型M和含水印模型M′各自局部窗口大小為p和q，兩個模型局部MSDM的距離定義如下：

LMSDM(p,q)

式中，L，C，S分別是曲率、對比度和結構之間的比較函數；μp和σp表示M模型局部窗口的均值和標準差；μq和σq表示M′模型局部窗口的均值和標準差；σpq表示M和M′模型局部窗口的協方差。

M和M′模型之間全局MSDM定義為n個局部MSDM之間的Minkowski和。MSDM值越小，表明兩個網格模型之間失真越小，視覺保真度也就越好。

水印嵌入強度直接影響含水印模型不可見性和魯棒性。文獻[28]指出當MSDM值在0.1以下時，三維網格模型失真度很小，具有很好的水印不可見性。兼顧考慮模型結構失真度以及水印抗網格攻擊魯棒性，在兩者之間進行折中，圖5分別表示避雷針和變壓器模型選取不同調節因子后水印嵌入前后的MSDM值，以MSDM 0.07左右為限，確定嵌入強度參數，見表2。

圖5 嵌入強度參數選取Fig.5 Embedding strong parameters selection

表2 水印嵌入前后模型間的MSDM值Tab.2 The values of MSDM

4.3 魯棒性分析

三維網格模型水印算法魯棒性的評價標準通常是以提取水印與原始水印的相關系數(Correlation Coefficient，COR) 的值為參考：

式中，w和分別是原始水印及其平均值；w′和分別是提取水印及其平均值。當含水印的模型未受到攻擊時，提取水印均有COR=1.0000。這說明本文水印算法能完全正確提取所嵌入的水印。相關系數COR的取值在[-1,1]之間。當相關系數大于某一設定的閾值T時，認為待檢測電力設備三維網格模型包含水印；否則不能證明包含水印。為了確定閾值，需求出隨機生成的水印信息和正確水印信息的相關值。通過大量實驗得到的最大相關值約為0.47[29]，所以本節將實驗閾值T設置為0.50。

（1）噪聲攻擊。含水印的模型在傳輸過程中常受到外部環境噪聲干擾等影響而成為含噪的三維網格模型。對已經含水印模型的頂點坐標加入均勻分布隨機噪聲，定義噪聲強度為模型頂點相對于到模型中心的平均距離的比值。網格噪聲攻擊后效果如圖6所示，抗噪聲攻擊實驗結果如圖7所示。可以看出算法對一定程度網格噪聲攻擊有較好的魯棒性。

圖6 噪聲攻擊效果圖Fig.6 Mesh noise attack map

圖7 抗網格噪聲能力Fig.7 Ability of resisting mesh noise attack

（2）仿射變換攻擊。當含水印網格模型遭受到平移、旋轉和均勻縮放等仿射變換時，模型位置、方向和尺度將發生改變，在提取水印前需要對受到此種類型攻擊的待檢測模型預先進行網格重定位，以便恢復與原始設備三維模型相同的位置、方向和比例。本文利用迭代最近點（Iterative Closest Point，ICP）對遭受到仿射變換攻擊的模型進行重定位，實現網格對齊[30]。實驗表明本文算法具有很好的抗幾何變換攻擊能力，結果見表3～表5。

表3 抗網格旋轉能力Tab.3 Ability of resisting mesh rotating attack

表4 抗網格平移能力Tab.4 Ability of resisting mesh translation attack

表5 抗網格均勻縮放能力Tab.5 Ability of resisting mesh uniform scale attack

（3）簡化攻擊。當網格模型遭受到簡化攻擊時，網格模型拓撲結構發生改變，本文利用網格重采樣技術將受攻擊模型恢復成原始模型拓撲結構[31-32]。網格簡化率為簡化掉的頂點數占原始模型總頂點數的百分比。簡化攻擊后網格效果如圖8所示，抗簡化攻擊實驗結果如圖9所示。可以看出該算法抗網格簡化攻擊能力較強。

圖8 簡化攻擊效果圖Fig.8 Mesh simplification attack map

圖9 抗網格簡化能力Fig.9 Ability of resisting mesh simplification attack

（4）剪切攻擊。網格剪切攻擊是網格模型連通性攻擊的另一種形式，與遭受到簡化攻擊類似，當含水印的網格模型遭受到剪切攻擊時，利用網格重采樣技術將受攻擊模型恢復成原始模型的拓撲結構關系。網格剪切率為裁剪的頂點數占原始模型總頂點數百分比。剪切攻擊后網格效果如圖10所示，抗剪切攻擊實驗結果見圖11。可以看出該算法對一定程度的網格剪切攻擊有較好的魯棒性。

圖10 剪切攻擊效果圖Fig.10 Mesh cropping attack map

圖11 抗網格剪切能力Fig.11 Ability of resisting mesh cropping attack

5 結論

本文提出一種電力設備自適應三維網格模型水印算法，通過對設備模型離散曲率估計，找出模型臍點位置。將網格模型頂點離散法向量和局部粗糙度相結合，構造符合人類視覺特性的嵌入強度函數，將水印自適應嵌入到網格臍點中。實驗結果表明，本文所提出的算法既能滿足電力設備網格模型的不可見性，又能保證設備模型抗攻擊的魯棒性。在深入研究網格模型曲率特征和不可見性的前提下，需要進一步改進算法抗網格連通性攻擊特性，并探索更有效的盲水印檢測算法。

致謝：感謝浙江理工大學孫樹森博士給予的指導和幫助。

[1] 孫鳳杰,崔維新,張晉保,等.遠程數字視頻監控與圖像識別技術在電力系統中的應用[J].電網技術,2005,29(5): 81-84.Sun Fengjie,Cui Weixin,Zhang Jinbao,et al.Application of remote digital video monitoring and image recognition technology in power system[J].Power System Technology,2005,29(5): 81-84.

[2] 胡炎,謝小榮,韓英鐸,等.電力信息系統安全體系設計方法綜述[J].電網技術,2005,29(1): 35-39.Hu Yan,Xie Xiaorong,Han Yingduo,et al.A survey to design method of security architecture for power information systems[J].Power System Technology,2005,29(1): 35-39.

[3] 胡炎,謝小榮,辛耀中.一種定量化的電力信息系統安全體系設計方法[J].電網技術,2006,30(2):7-13.Hu Yan,Xie Xiaorong,Xin Yaozhong.A quantitative security architecture design method for power information system[J].Power System Technology,2006,30(2): 7-13.

[4] 傅書逷.2007年IEEE PES學術會議電網調度自動化部分綜述與討論[J].電網技術,2008,32(5): 31-37.Fu Shuti.Summary and discussion on 2007 IEEE PES general meeting (power system dispatch automation part)[J].Power System Technology,2008,32(5):31-37.

[5] 尹浩,林闖,邱鋒,等.數字水印技術綜述[J].計算機研究與發展,2005,42(7): 1093-1099.Yin Hao,Lin Chuang,Qiu Feng,et al.A survey of digital watermarking[J].Journal of Computer Research and Development,2005,42(7): 1093-1099.

[6] 劉巖,伍祥生,鄭東,等.基于相位信息的旋轉、縮放、位移不變的圖像水印技術[J].中國電機工程學報,2005,25(10): 89-96.Liu Yan,Wu Xiangsheng,Zheng Dong,et al.Phase information in RST invariant image watermarking[J].Proceedings of the CSEE,2005,25(10): 89-96.

[7] 涂蓉暉,趙繼英.基于小波變換和量化理論的半脆弱數字聲音水印算法及在電力系統中的應用[J].中國電機工程學報,2005,25 (12): 78-85.Tu Ronghui,Zhao Jiying.A semi-fragile audio watermarking scheme based on digital wavelet transform and quantization and its application in power system[J].Proceedings of the CSEE,2005,25(12): 78-85.

[8] 王先培,游文霞,王泉德,等.數字水印技術在電力系統文檔可信傳輸中的應用[J].電力系統自動化,2002,26(18): 61-64.Wang Xianpei,You Wenxia,Wang Quande,et al.Application of digital watermarking technique to credible delivery of documents in power systems[J].Automation of Electric Power Systems,2002,26(18):61-64.

[9] 吳軍基,盛琪,賀濟峰,等.小波數字水印在電力系統信息安全中的應用[J].電力自動化設備,2004,24(12): 40-42.Wu Junji,Sheng Qi,He Jifeng,et al.Application of wavelet-based digital watermark in power system information security[J].Electric Power Automation Equipment,2004,24(12): 40-42.

[10] Ohbuchi R,Masuda H,Aono M.Embedding data in 3D models[C].European Workshop on Interactive Distributed Multimedia Systems and Telecommunication Services,Darmstadt,1997: 1-10.

[11] Lee S H,Kwon K R.Mesh watermarking based projection onto two convex sets[J].Multimedia Systems,2008,13(5-6): 323-330.

[12] 張朝輝,劉文予,鄭玉婷,等.局部集的3D模型水印方法[J].中國圖象圖形學報,2009,14(7):1298-1306.Zhang Chaohui,Liu Wenyu,Zheng Yuting,et al.Watermarking 3D objects using local set information[J].Journal of Image and Graphics,2009,14(7): 1298-1306.

[13] Yu Zhiqiang,Horace H S Ip,Kwok L F.A robust watermarking scheme for 3D triangular mesh models[J].Pattern Recognition,2003,36(11): 2603-2614.

[14] 廖學良,王瑀屏.一種新的三維模型水印嵌入空域算法[J].計算機學報,2008,31(10): 1848-1856.Liao Xueliang,Wang Yuping.A new spatial domain method for watermarking in 3D Models[J].Chinese Journal of Computers,2008,31(10): 1848-1856.

[15] Kanai S,Date H,Kishinami T.Digital watermarking for 3D polygons using multiresolution wavelet decomposition[C].International Workshop on Geometric Modeling,Tokyo,1998: 296-307.

[16] Ohbuchi R,Mukaiyama A,Takahashi S.A frequencydomain approach to watermarking 3D shapes[J].Computer Graphics Forum,2002,31(2): 373-382.

[17] Cayre F,Rondao-Alface P,Schmitt F,et al.Application of spectral decomposition to compression and watermarking of 3D triangle mesh geometry[J].Signal Processing,2003,18(4): 309-319.

[18] 方惠蘭,王國瑾.三角網格曲面上離散曲率估算方法的比較與分析[J].計算機輔助設計與圖形學學報,2005,17(11): 2500-2507.Fang Huilan,Wang Guojin.Comparison and analysis of discrete curvatures estimation methods for triangular meshes[J].Journal of Computer-aided Design &Computer Graphics,2005,17(11): 2500-2507.

[19] Moreton H P,Sequin C H.Functional optimization for fair surface design[C].19th ACM Annual Conference on Computer Graphics and Interactive Techniques,New York,1992: 167-176.

[20] Taubin G,Kobbelt L.Geometric signal processing on large polygonal meshes[C].ACM Conference on Computer Graphics,Log Angeles,2001,Course 17.

[21] Petitjean S.A survey of methods for recovering quadrics in triangle meshes[J].ACM Computing Surveys,2002,34(2): 211-262.

[22] Cohen-Steiner D,Morvan J M.Restricted delaunay triangulations and normal cycle[C].19th ACM Annual Symposium in Computational Geometry,San Diego,2003: 237-246.

[23] Rondao P Alface,Macq B.Blind watermarking of 3D meshes using robust feature points detection[C].IEEE Conference on Image Processing,Italy,2005:693-696.

[24] 孫樹森.三維模型數字水印技術及防重構技術研究[D].杭州: 浙江大學,2006.

[25] Ashourian M,Enteshary R.A new masking method for spatial domain watermarking of three-dimensional triangle meshes[C].IEEE Conference on Convergent Technologies for the Asia-Pacific Region,Bangalore,2003: 428-431.

[26] Guillaume Lavoué.A local roughness measure for 3D meshes and its application to visual masking[J].ACM Transactions on Applied Perception,2009,5(4): 21.

[27] 朱少敏,劉建明.特高壓設備三維網格模型自適應量化水印算法[J].電網技術,2010,34(11): 6-11.Zhu Shaomin,Liu Jianming.An adaptive watermarkquantifying algorithm for 3-D meshs model of ultra high voltage equipment[J].Power system technology,2010,34(11): 6-11.

[28] Cignoni P,Rocchini C,Scopigno R.Metro:measuring error on simplified surfaces[J].Computer Graphics Forum,1998,17(2): 167-174.

[29] Lavoué Guillaume,Gelasca E D,Dupont F,et al.Perceptually driven 3D distance metrics with application to watermarking[C].Proceedings of SPIEThe International Society for Optical Engineering,2006.

[30] Kai Wang,Guillaume Lavoué,Florence Denis,et al.Hierarchical watermarking of semiregular meshes based on wavelet transform[J].IEEE Transaction on Information Forensics and Security,2008,3(4):620-634.

[31] 周昕.三維幾何模型數字水印技術及算法研究[D].杭州: 浙江大學,2002.

[32] Besl P J,McKay N D.A method for registration of 3-D shape[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1992,14(2): 239-256.

[33] Jerome Maillot,Hussein Yahia,Anne Verroust.Interactive texture mapping[C].20th ACM Annual Conference on Computer Graphics and Interactive Techniques,Anaheim,1993: 27-34.

[34] Emil Praun,Hugues Hoppe,Adam Finkelstein.Robust mesh watermarking[C].26th ACM Annual Conference on Computer Graphics and Interactive Techniques,Los Angeles,1999: 49-56.