高精度多徑時延估計

付龍飛，張水蓮，辛 剛

(解放軍信息工程大學，河南 鄭州 450002)

多徑時延參數是無線信道的重要參數，是反映無線信道通信質量的關鍵指標之一。多徑時延參數的估計是現代信號處理領域非常活躍的研究課題，廣泛地應用于通信、雷達、地質勘探等領域。匹配相關是估計信道多徑時延的經典方法，具有高魯棒性、低計算量等優點。但隨著多徑相對時延的減小，匹配相關法的性能會急劇下降，由于時延可分辨的條件是時延寬帶積大于等于1，即使在理想信道的情況下，其分辨力的極限是信號帶寬的倒數。為了突破匹配相關法的分辨力極限，人們提出了基于代價函數的時延估計方法。最小均方誤差法(MMSE)、極大似然法(ML)以及非線性最小乘法(NLS)均是典型的基于代價函數的估計方法。這些方法能夠實現超分辨力估計，即能夠分辨時延小于信號帶寬倒數的多徑信號。但是，基于代價函數的時延估計方法涉及到多維參數優化的問題，計算量龐大，實時性不夠理想。隨著多徑時延估計方法研究的深入，人們將陣列信號處理的方法應用于多徑時延估計，建立了基于特征子空間分解的時延估計方法[1-4]。基于MUSIC算法的多徑時延估計方法便是其中的杰出代表。本文針對無線信道多徑時延的特點，提出一種基于MUSIC和root MUSIC算法的簡單易行的高精度信道多徑參數估計方法，把時域的時延問題轉換到頻域內，利用MUSIC和root MUSIC算法具有高頻譜分辨率這一特性[5]，進而得到高精度的信道多徑時延參數。

1 數據模型

接收信號的離散模型可表示為：

其 中 ，s(n)表 示 發 送 的 信 號 序 列 ，λl(n)和 τl(l=1,…,L)分別表示第l條路徑上信道對發送的信號序列所施加的調制和時延，υ(n)是白高斯噪聲。一般情況下，若信號序列較短，信號在信道傳輸過程中，λl(n)可以認為是一個常數。于是，式(1)可以寫成如下的形式:

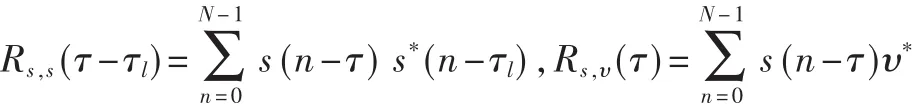
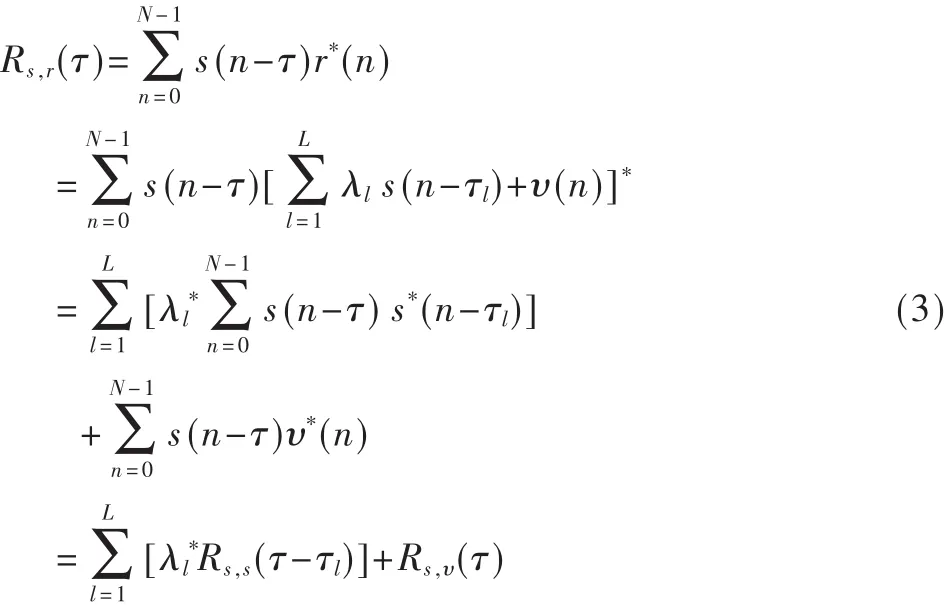
式中，(n)，N表示相關值的數據長度。

對式(3)進行N點的 DFT，可得:

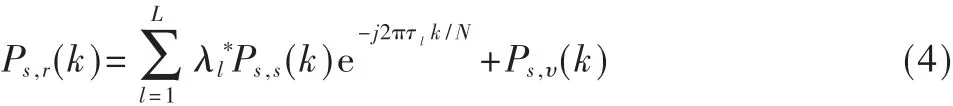
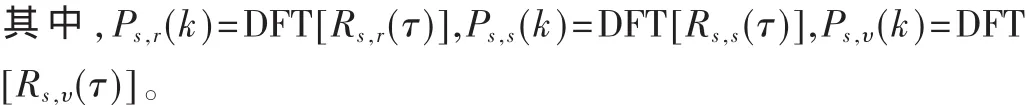
在式(4)中，令n(k)=Ps,υ(k)，統一等效成信號的噪聲。雖然Ps,υ(k)不再是白噪聲，但在信噪比較大的情況下，對估計性能不會產生很大的影響。

將式(5)寫成矩陣的形式:

其中，

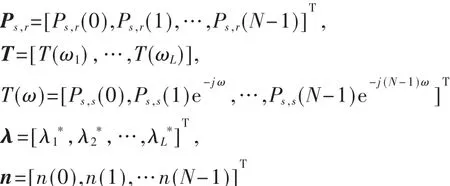
現在只需要證明T是列滿秩，就可以建立近似等距多元線陣的數據模型，進而采用MUSIC算法，對T中的頻率分量進行估計，再通過式(5)完成各時延的估計。在該近似等距多元線陣模型中，λ可以認為是不相干的遠場窄帶信號，Ps,r可以認為是一次快拍信號。其實，T是滿秩的條件很容易滿足。對T進行分解可得：

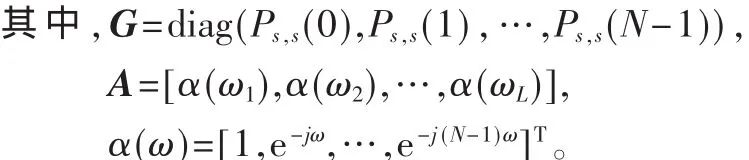
由于A是一個列滿秩的Vandermonde矩陣，只要第一部分的秩(即對角矩陣G非零元素的個數)大于第二部分的秩 (即 Vandermonde矩陣 A的列數)，T就是一個滿秩的矩陣。在實際情況下，這樣的條件一般是滿足的。而且，矩陣G對角線上的元素構成了信號s(n)的功率譜，一般情況下呈現低通性，為第3部分基于單次測量數據的時延估計分析奠定了良好的基礎。

通過多次“快拍”Ps,r估計出它的相關矩陣 RP=E{Ps,r}，進而對其進行特征值分解得到由噪聲特征向量所組成的矩陣C。根據MUSIC算法的原理，式(6)中的T與噪聲特征向量所組成的矩陣C正交，即:

式(10)極大值出現的位置即為 T中ωl(l=1,…L)的估計。與經典 MUSIC算法的不同是，此時 T(ω)=[Ps,s(0),Ps,s(1)e-jω，…,Ps,s(N-1)e-j(N-1)ω]T，即 存 在 一 個 低 通 包 絡 。

下面分析將root MUSIC算法應用上述模型的合理性。

root MUSIC算法是MUSIC算法的一種多項式求根形式,于1983年由Barabell提出，其基本思想是Pisarenko分解[6]。

對式(10)求倒數，并聯立式(7)得到：

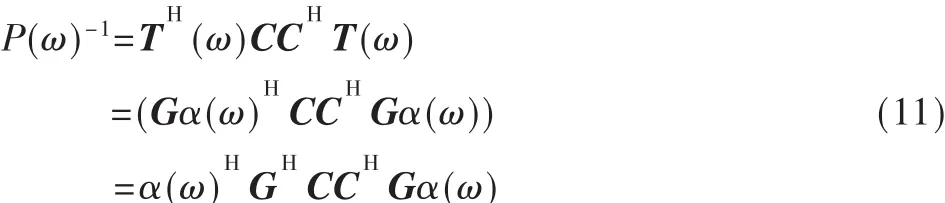
令 O=[Om,n]N×N=GHCCHG,則有：

式(8)的等價含義是，T中的每個列向量都與C正交。因為T的每個列向量均有相同的形式，于是對T中頻率分量進行估計的問題可以轉化為求下式零點的問題:

式(9)的另一個等價形式表示為:

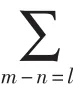
于是，式(10)極值的估計問題可以轉化成為式(13)在單位圓上根的估計問題。通過式(13)求出離單位圓最近的并關于單位圓對稱的L對根。這些根的相位即對應式(8)中 ωl(l=1,…L)的估計。

2 基于單次測量數據的多徑時延估計

在前面的推導中，對“快拍”數據Ps,r的自相關矩陣的估計需要用到多次測量的數據，并且要求各傳輸路徑的調制系數 λ=[,…,]T不相關。但很多情況下，多徑信道隨著時間的推移其多徑參數會發生顯著變化。譬如多徑的條數以及時延發生了變化，上述的模型將不再適用于多徑時延估計。另外一個必須注意的問題是，如果各傳輸路徑鄰近，則它們的調制系數λl(n)(l=1,…L)可能存在著強相關性，這種強相關性也使得多次測量的數據沒有什么意義。因此，通過分析單次測量的數據來估計多徑時延更具有實際意義。

為了克服遠場信號的相干性，人們提出了空間平滑技術。通過空間平滑，可以構建一個縮小了孔徑的多元線陣模型。針對單次測量的數據，將空間平滑的技術移植到本文所提出的模型同樣適用，即可以通過空間平滑技術得到一個較小的自相關矩陣RP=E{Ps,r,}。 但是本文提出存在一個低通的包絡，會對空間平滑估計的性能產生不利影響。然而，BESSON和STOICA指出[7],在包絡變化平緩的情況下，信號子空間與噪聲子空間的匹配程度只是稍有下降，即MUSIC的估計性能只是稍有降低，仍然可以用于高精度地估計式(6)中的頻率分量，從而估計多徑時延。

其中，RP(Δk)表示Ps,r(k)的自相關函數的估計序列。得到Ps,r(k)自相關函數的估計RP(Δk)之后，可采用參考文獻[8]的思想完成基于單次探測數據的自相關矩陣的估計，令自相關矩陣的估計為：

其中，M可以認為是縮小了孔徑的陣元數，應充分小于單次測量數據的長度N；式(15)中的元素為:當i≥j時，有Rij=RP(i-j)；當i＜j時，有Rij=。從統計的角度講，式(15)中的M越小，更接近于自相關矩陣的真實值[9]；從陣列信道處理的角度講，M越大，相當于陣元越多，分辨率越高。二者對立統一，如何選擇M的大小，在工程應用中需要針對不同的通信序列具體分析。

但本文采用另外一種方法來構建基于單次測量數據的自相關矩陣。 由式(3)和(4)可知，Ps,r(k)是Rs,r(τ)的傅里葉變換，它們均是長度為N的序列。若將它們看作隨機變量的采樣值，存在如下關系：

對照式(11)到式(13)，基于單次實驗數據所推導的模型同樣適用于root MUSIC算法，這里不再贅述。

3 仿真

下面的仿真結果均基于單次測量的數據。仿真的信號是頻率為f(t)=flower+βt(0≤t≤T)的正弦波,即 Chirp序列。 在這里，β=(fupper-flower)/T，flower和fupper分別對應在時間區間0≤t≤T內的起始頻率和終止頻率，仿真信號的帶寬為B=。 仿真條件為flower=0 Hz，fupper=4×104Hz，采樣頻率fs=8B=8fupper，T=511/fs， 式 (15)中的M=roundround(x)表示取離x最近的整數。仿真的多徑條數為2,時延相差4個采樣點。

圖1是信噪比為0 dB時接收的信號與本地參考信號匹配相關的結果，由于4/fs＜1/B，即相對多時延小于信號帶寬的倒數,匹配相關后不能得到任何的多徑信息。

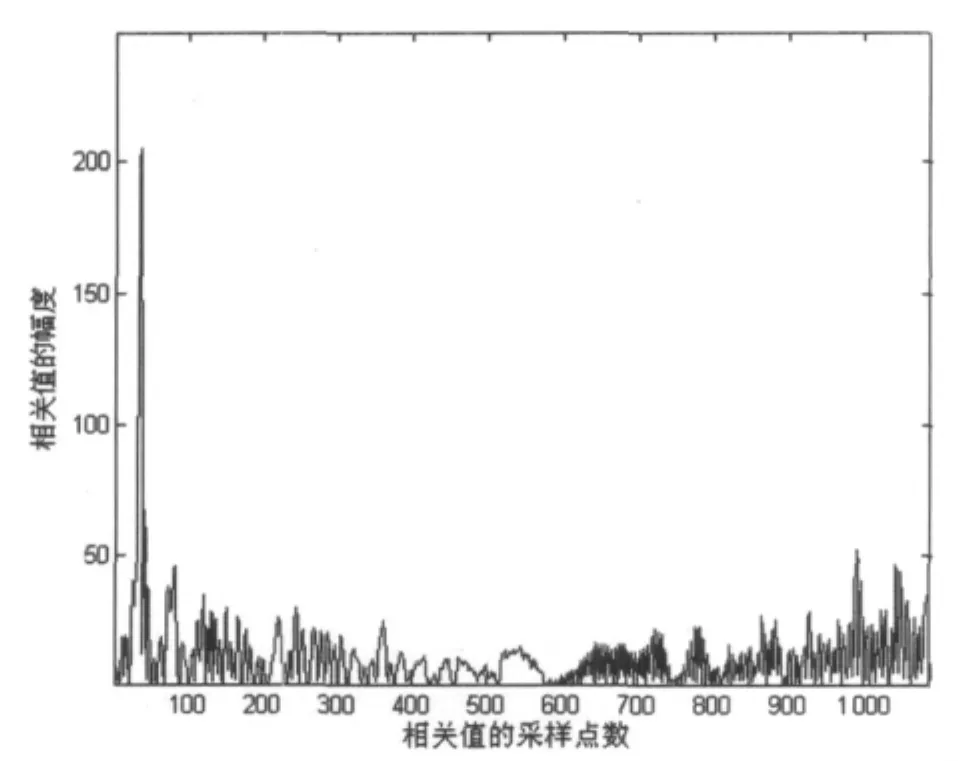
圖1 接收的信號與本地參考信號匹配相關的結果

圖2是由基于本文模型的MUSIC算法和root MUSIC得到的仿真結果,信噪比仍為0 dB。曲線的兩個峰值分別對應通過MUSIC算法得到的由兩條多徑時延所產生的頻率的估計，兩個星號對應由root MUSIC算法得到頻率估計，兩箭頭表示由實際時延所生的頻率分量。由此可以看出，通過本文提出的算法，即使基于單次測量的數據，也能夠高精度地估計式(6)中T的頻率分量，從而得到準確的時延估計。

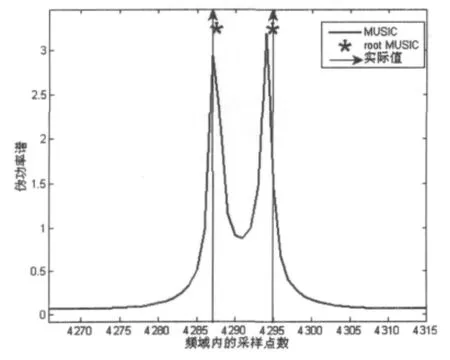
圖2 MUSIC和root MUSIC算法進行時延估計的結果

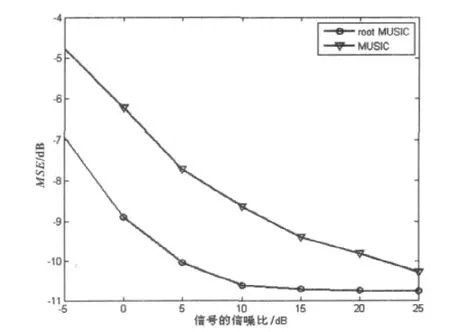
圖3 MUSIC和root MUSIC算法估計性能比較

提出了一種多徑時延模型，將時延問題轉化成為頻譜估計的問題。該問題的實質是，完成存在低通包絡情況下的頻率分量估計。建立相應模型之后，再利用具有高頻率分辨力的MUSIC算法以及root MUSIC算法完成對時延的高精度估計。分析了基于單次測量數據的時延估計，并對其進行了仿真。仿真結果表明，本文提出的方法對時延具有超分辨力；在相同的條件下，root MUSIC算法比MUSIC有更好的估計性能；由于低通包絡的影響,基于單次測量數據的時延估計是一個有偏估計。

[1]王巍,熊瑾煜,朱中梁.CDMA信號碼片內多徑時延估計算法[J].電子與信息學報，2004,26(9):1345-1450.

[2]黎英云.微弱多徑信號時延估計技術研究[D].武漢：華中科技大學，2009.

[3]Ge Fengxiang,Shen Dongxu,Peng Yingning,et al.Superresolution time delay estimation in multipath enviroments[J].IEEE Transactions on Circuit and Systems-I,September 2007,54(9):1977-1986.

[4]SAANRNISSARI H.TLS-ESPRIT in a time delay estimation[C]//Proceedings of IEEE 47th Vehicular Technology Conference.Phoenix,USA,1997:1619-1623.

[5]SCHMIDT R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation,March 1986,AP34(13):276-280.

[6]BARABELL A J.Improving the resolution performance of eigenstructure based direction-finding algorithms[C].Proceedings of International Conference on Acoustics,Speech and Signal Processing.Boston,USA,1983:336-339.

[7]BESSON O,STOICA P.Analysis of MUSIC and ESPRIT frequency estimates for sinusoidal signals with lowpass envelopes[J].IEEE Transactions on Signal Processing,1996,44:2359-2364.

[8]REN Q S.WILLIS A J.Extending MUSIC to single snapshot and online direction finding applications[C].Record of IEEE International Radar Conference,Publ.No.449.Edinburgh,UK,1997:773-787.

[9]王世一.數字信號處理(修訂版)[M].北京：北京理工大學出版社,1997.