適用于低滾降系數成型脈沖的定時恢復方案

黃 磊，許 科，崔慧娟，唐 昆

（清華大學 電子工程系 清華信息科學與技術國家實驗室，北京 100084）

位同步是進行可靠數字通信的關鍵環節。按照定時誤差提取方式分類，位同步算法可以分為DA(數據輔助)和NDA(非數據輔助)。相對于DA類算法，NDA類算法不需要引導符號，可以實現更高的帶寬有效性，付出的代價是相對較高的估計方差。按照數據處理結構分類，可以分為前饋估計和反饋估計。傳統的基于鎖相環(PLL)結構的定時估計器都屬于反饋估計，由于反饋結構內在特性，使其更容易出現 Cycle Slip和 Hang up[1]現象。本文主要關注NDA前饋定時估計算法。

[2]中提出了一種廣泛使用的平方定時估計算法，平方定時估計器基于調制信號的二階循環平穩統計特性，當成型脈沖的滾降系數較小時，會帶來較大的估計方差，本文針對這一問題給出了改進的方法。

1 信號模型和二階循環平穩特性分析

本文采用標準的脈沖疊加模型，其離散時間版本如下式所示：

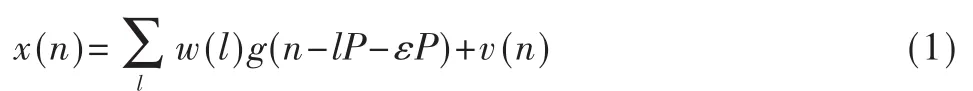
w(l)表示獨立同分布符號序列，為了便于分析，不妨假設其方差為1;g為成形脈沖，這里采用升余弦成形脈沖，滾降系數為ρ;P表示每個符號采樣點數，P取足夠大，以保證采樣信號不引起混疊;ε表示定時信息，0＜ε＜1；v(n)為獨立同分布白高斯噪聲。

信號的二階自相關可以用下式表示：

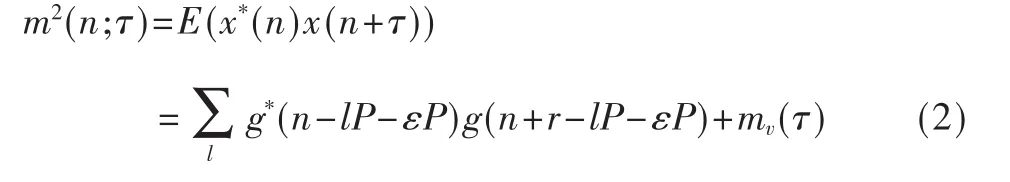
其中mv(τ)表示噪聲的二階自相關。從上式可以看出，信號的二階自相關函數是關于P的周期函數，二階自相關是循環平穩的，所以可以對其求取傅里葉級數，如下式：

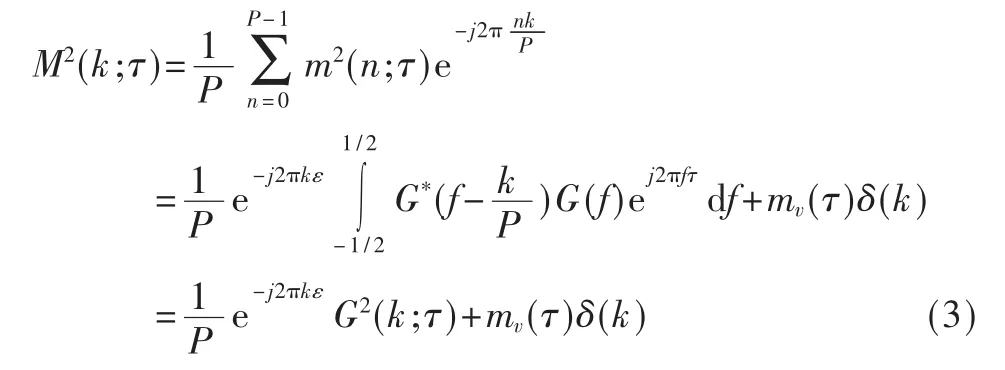
G(f)是成型脈沖的 DTFT(離散時間傅里葉變換)，可以看出只要對M2(k;τ)求角就可以求出定時信息。

經典的平方定時估計器[2]可以看作是對M2(1;0)的估計，如下式所示：

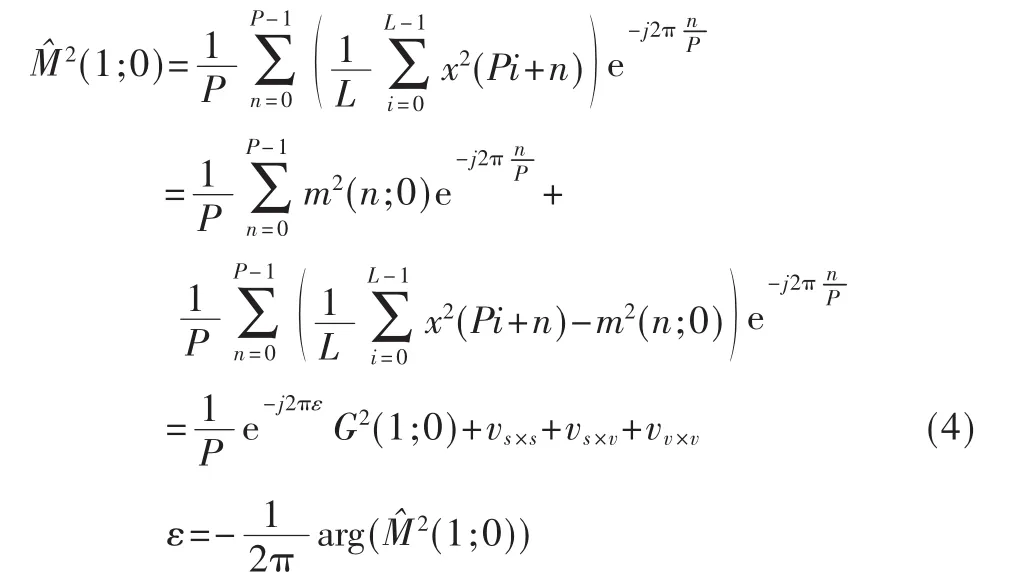
其中 vs×s+vs×v+vv×v表示由自相關估計導致的自噪聲、信號與加性噪聲導致的互噪聲及加性噪聲的總和。從上式可以看出，定時誤差估計變成了一個在加性噪聲情況下的相位估計，因此當噪聲一定的情況下信噪比主要由G(1;0)決定。對于滾降系數為ρ的升余弦成型脈沖來說，可以得到：

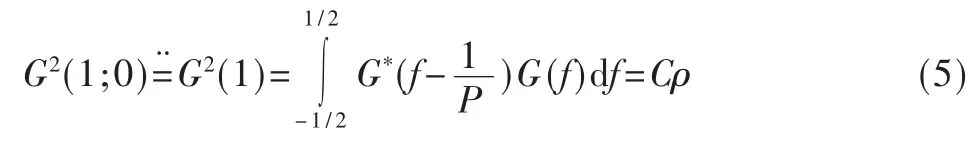
C是一個常量，G2(1;0)與 ρ呈線性關系。當 ρ->0，也就是成形脈沖趨近于Nyquist脈沖時，平方估計法甚至會失敗。

2 基于絕對值的定時誤差估計器

對于低滾降系數成形脈沖來說，可以采用基于絕對值的定時誤差估計器，如下式：

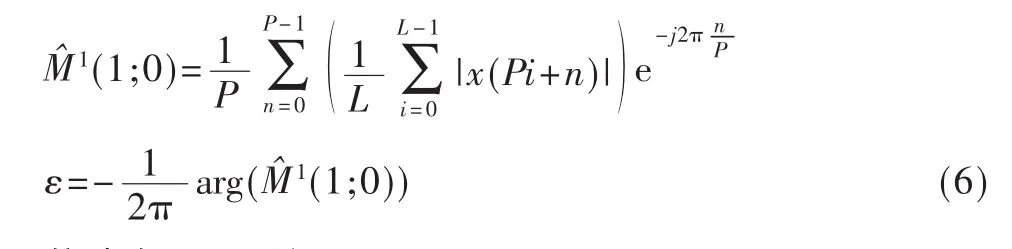
仿真如圖1所示。

圖1中最下面的曲線是定時估計的MCRB(修正的可拉美羅界)[3]。圖1(a)、圖1(b)分別對應滾降系數為 0.1和 0.5的 QPSK 調制，分析窗長 L=100時的 MSE=E(ε-)2，可以看出在低滾降系數下，絕對值非線性有明顯的性能增益。隨著滾降系數的增大，其性能趨于平方非線性。

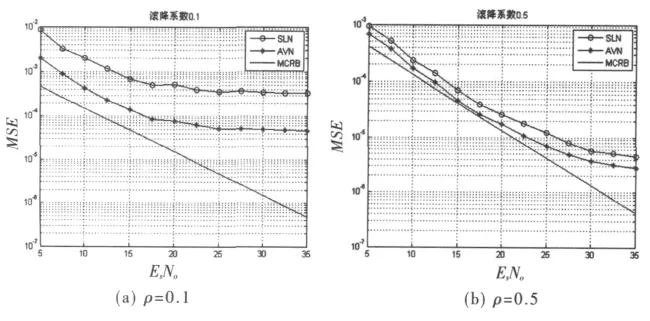
圖1 ρ=0.1和 0.5時定時估計均方差與EsNo的關系

其實基于絕對值的定時估計器是基于高階統計量的定時估計器的特例。對于偶對稱無記憶非線性函數，其多項式擬合只包括輸入的偶次冪。如式(7)所示：

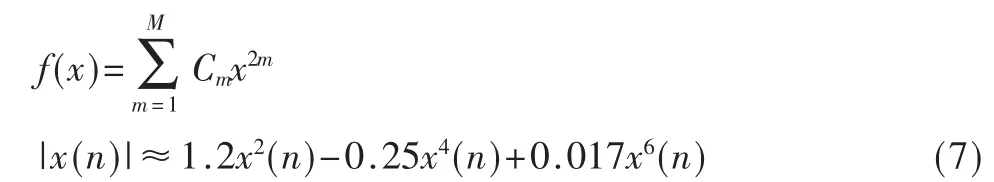
E(x2m(n))同E(x2(n))一樣也是循環平穩隨機過程，周期為P，運用傅里葉級數可以得到下式：

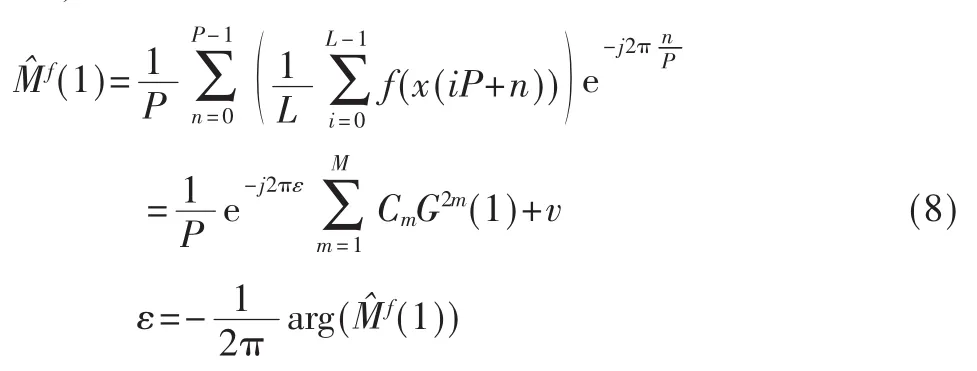
G2m(1)由于解析式太過復雜，可以通過仿真的方法得到，仿真時令ε=0，噪聲為0，然后用充分長的序列去估計信號的高階距，最后進行FFT得到處的值。滾降系數與G(1)的關系如圖2所示，矩估計噪聲與EsNo的關系如圖3所示。

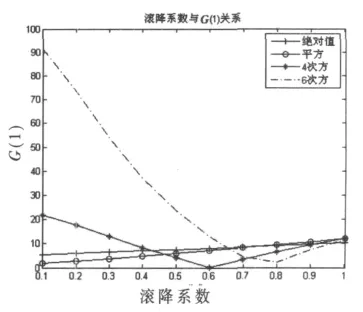
圖2 滾降系數與G(1)關系

從圖2、圖3中可以看出，隨著冪次的升高G2m(1)在增大，但是付出的代價是平均矩估計噪聲增大，所以只有選擇合適加權系數才能實現性能增益。從圖2和圖3中對比絕對值和平方非線性，絕對值非線性在滾降系數0.1～0.4之間時G(1)值要高于平方非線性，但是平均矩估計噪聲并沒有顯著增加，兩者的結合使絕對值非線性在低滾降系數下性能更好。絕對值的G(1)隨著滾降系數的增大趨近于平方非線性，在ρ=0.5時兩者已經接近。這也與圖1仿真是一致的。

3 預濾波和卡爾曼濾波后處理

采用預濾波[4]的方法可以有效降低信號的定時方差，這里采用如下的預濾波器，如下式：

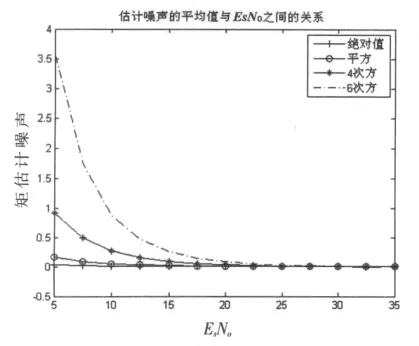
圖3 矩估計噪聲與EsNo的關系

預濾波和后濾波整體頻域響應如圖4所示。增加預濾波之后的仿真性能如圖5所示。

圖4 信道濾波和預濾波整體響應

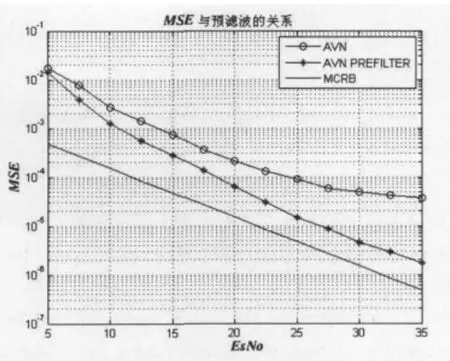
圖5 增加預濾波器之后的估計性能ρ=0.1

從圖4中可以看出增加預濾波器之后，整體傳輸特性呈現為一個中心頻率在的帶通濾波器，通過這個濾波特性提高了在G(1)處的信噪比，改善了估計性能。

除了預濾波之外，基于一階卡爾曼濾波器的后濾波器可以用來解決定時回繞(Unwrapper)和平滑估計噪聲。本文采用參考文獻 [5]中的一階卡爾曼后濾波器結構。通過后濾波可以解決當連續變化的ε超過-0.5和0.5造成的估計反轉問題,同時對輸出進一步平滑。如圖6、圖7所示。

本文從信號的循環平穩統計特性入手，分析了傳統的平方定時估計器在低滾降系數成型脈沖條件下性能下降的原因。指出絕對值非線性更適合于嚴重帶限信號，絕對值非線性的性能增益源于其可以看作信號高階矩的加權和，高階矩的引入改善了由于滾降系數降低帶來的性能損失。最后本文指出采用基于頻移成型脈沖的預濾波和基于一階卡爾曼濾波器的后濾波可以有效降低估計方差。預濾波、絕對值非線性和后濾波三者的結合使用可以作為低滾降系數成型脈沖條件下一種合理的定時恢復方案。

參考文獻

[1]GERD ASCHEID HEINRICH MEYR.Cycle slips in phaselocked loops:a tutorial survey[J].IEEE Trans.on Comm,1982,COM-30(10).

[2]Martin oerder heinrich meyer digital filter and squre timing recovery[J].IEEE Trans.Comm,1988,136(5).

[3]ALDO N,ANDREA D,MENGALI U.Ruggero reggiannini the modified cramerrao bound and its applicatopm to synchronization Problems.IEEE Trans.Comm,1994,42(21314).

[4]Shi Kai,PRADEEP K.Sarvepalli and erchin serpedin on the design of digital blind feedforward jitter free timing recovery schemes for linear modulations[J].IEEE Trans.on Comm,2004,52(9).

[5]李光源，黃磊，崔慧娟，等.改進的非數據輔助前向反饋符號定時恢復算法[J].電視技術，2011(1):48-50,56.