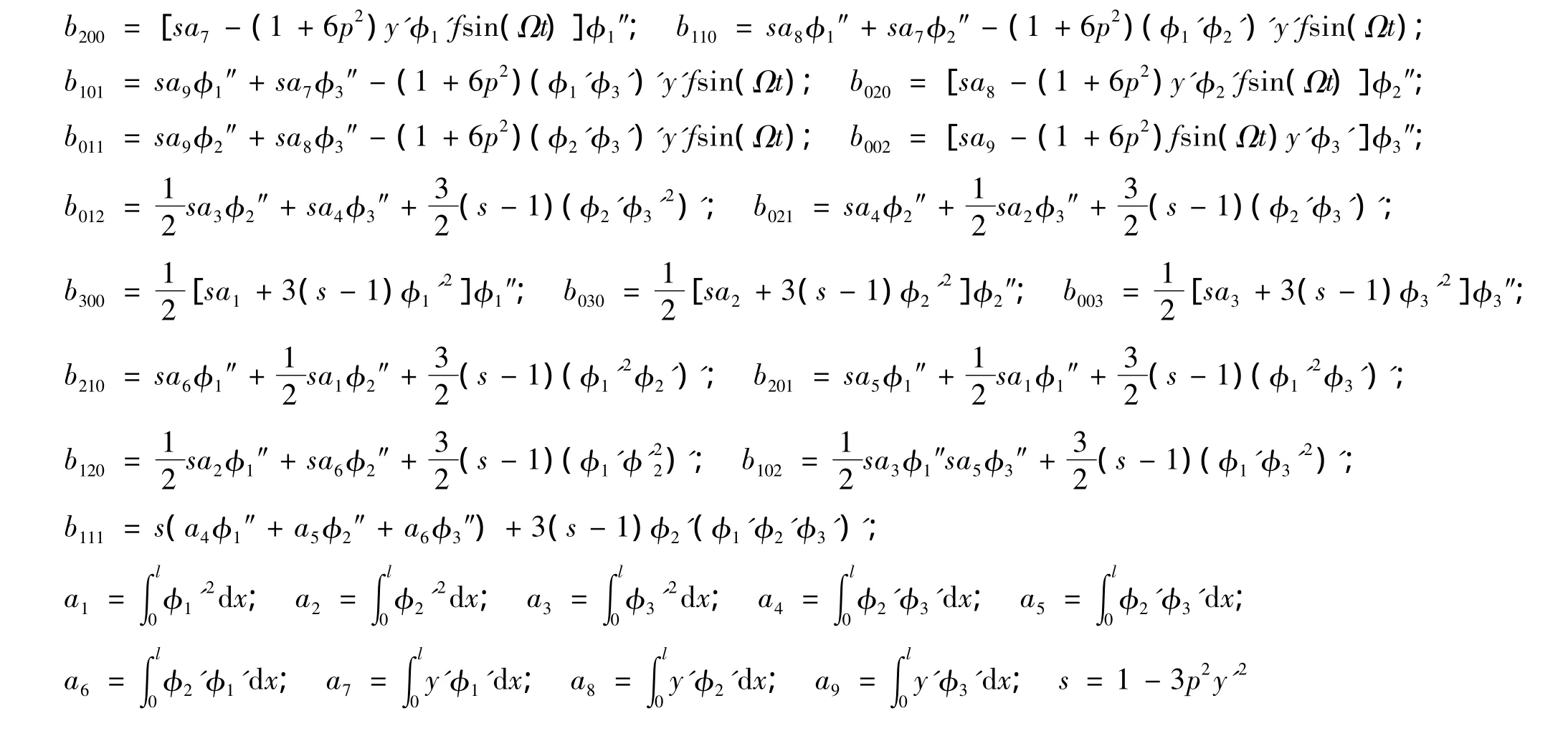橫向補給系統高架索在一重和雙重內共振下的面內振動

張良欣，何學軍，任愛娣

(海軍工程大學 后勤指揮與工程系，天津 300450)

高架索在橫向干貨補給過程中，由于受到集中質量(貨物)在高架索上的位置的變化、高架索兩端高度差以及船舶運動引起的索端的激勵等因素的影響，使得高架索系統的動力學行為異常復雜。目前對于橫向干貨補給系統的高架索研究還主要局限于靜力學、結構計算及優化設計等方面［1－4］，對于作為橫向補給高架索系統的控制設計基礎的動力學特性的研究還很少。橫向補給高架索系統的動力學模型可以近似簡化為具有集中質量的傾斜懸索，其動力學特性研究可借鑒類似懸索的動力學研究成果。陳自力，唐駕時［5］針對工程客、貨運索道系統，利用δ函數來體現集中載荷對懸索的影響，建立了外激勵作用下、具有移動集中載荷的兩端固定的水平懸索的動力學模型;通過利用Galerkin離散與多尺度方法對系統進行漸近分析，得到了系統主共振/次共振分岔點的解析解、分岔點位置以及相應分岔圖，還分析了系統的分岔和穩定性。Lin和Perkins［6］建立了具有若干集中質量懸索的三自由度線性振動模型，提出了可用于求解任意垂度懸索特征解的半解析半數值的方法，拓展了以往分析懸索—質量系統動力學受限于模態階數的理論方法。Rega等［7］對傾斜懸索的動力學特性進行深入研究，研究表明其面內振動的模態頻率與水平懸索存在本質區別，傾斜懸索不存在對稱和反對稱模態，其模態形式為混合型(非對稱)模態。模態頻率與彈性—幾何參數關系也不象水平懸索那樣對稱與反對稱模態頻率存在交叉點，而是各階模態頻率曲線分離。Takahashi［8］參照Irvine［9］水平懸索線性頻率計算公式，考慮懸索傾斜角度的影響，推導出用于計算傾斜懸索頻率的改進的Irvine公式，并與Galerkin離散結果、Irvine理論結果比較，結果表明，改進的Irvine公式具有很高的精度。本文綜合上述文獻的建模思想，考慮到集中質量等因素的影響，建立了高架索的面內振動理論模型。利用Galerkin方法對系統進行了離散，得到了高架索系統的前3階模態振動的標準控制方程。借助Mathematica軟件，分析了集中質量在高架索上的位置對系統各階模態頻率的影響;同時，利用數值方法對1∶1∶2雙重內共振及1∶2內共振兩種情況下系統的面內振動特性進行分析。

1 控制方程建立及簡化

綜合文獻［4］－文獻［9］，考慮到集中質量在高架索上的位置對系統的動力學行為的影響，高架索系統平面內振動的動力學模型為:

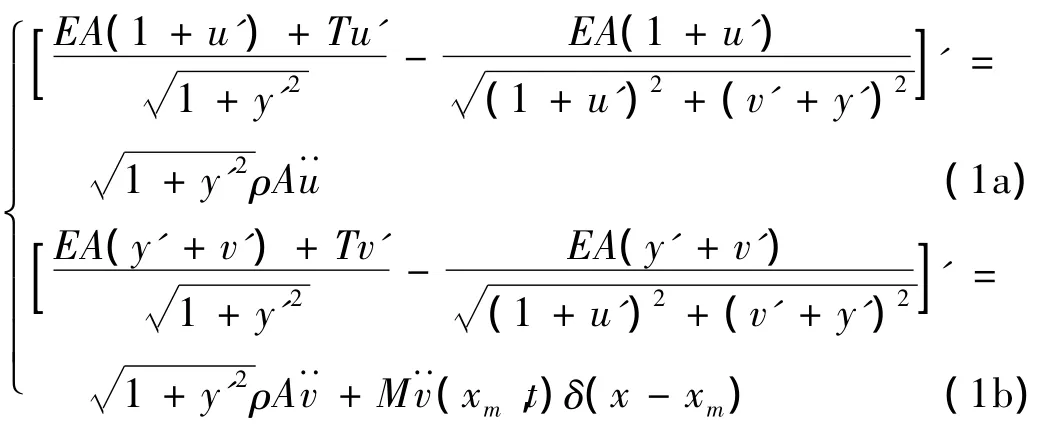
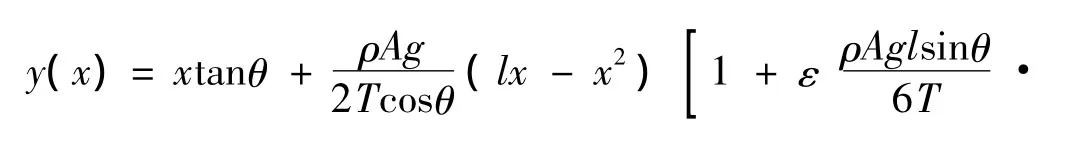
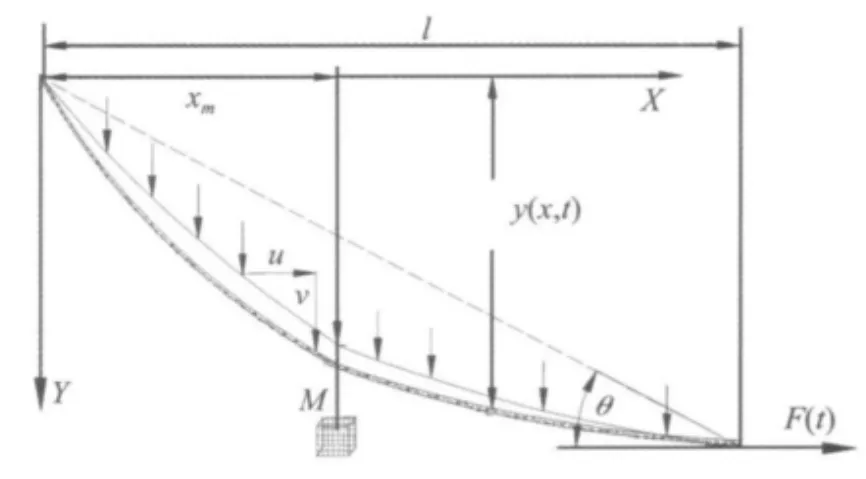
圖1 高架索系統的示意圖Fig.1 The schematic model of highline cable

為了研究高架索系統的面內橫向振動，將高架索的軸向運動做為激勵簡化高架索面內控制方程。考慮參數激勵情況，根據邊界條件［10］u(0，t)=0，u(l，t)=lF(t)，對方程(1a)分別進行邊界積分，得:

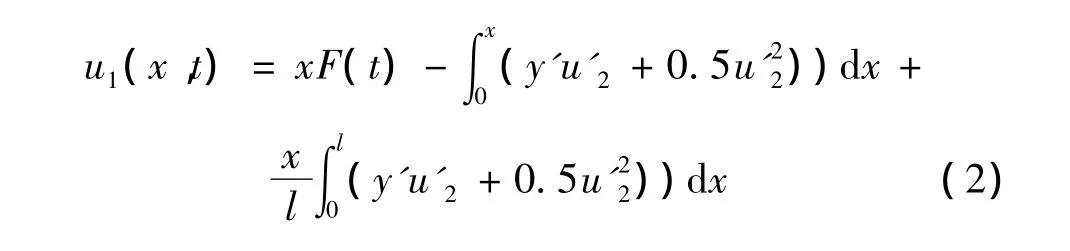
將式(2)代入式(1b)，可得高架索系統的面內橫向振動的控制方程:

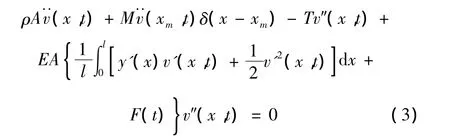
式中F(t)=f sin(Ωt)為高架索的索端無量綱參數激勵，f為無量綱常數，Ω為激勵頻率。

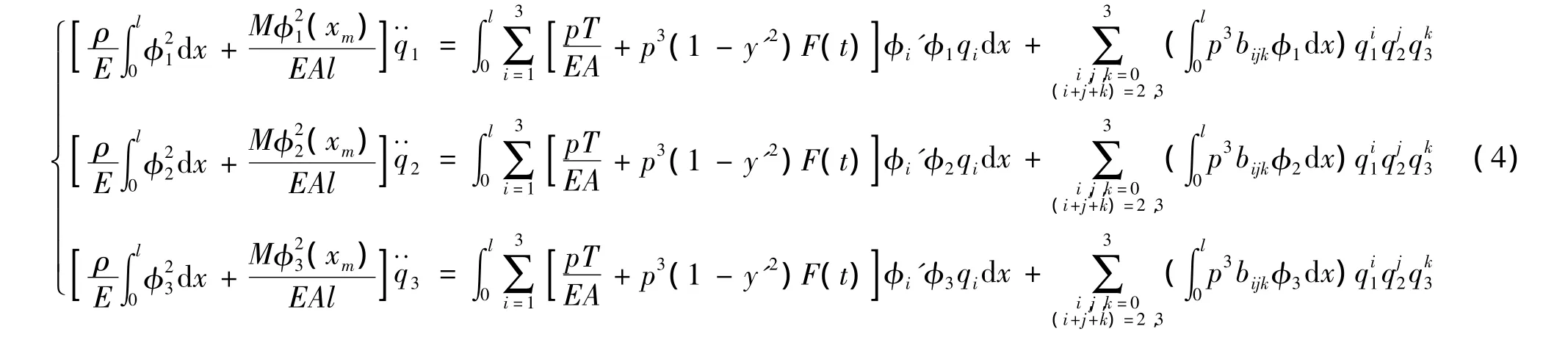
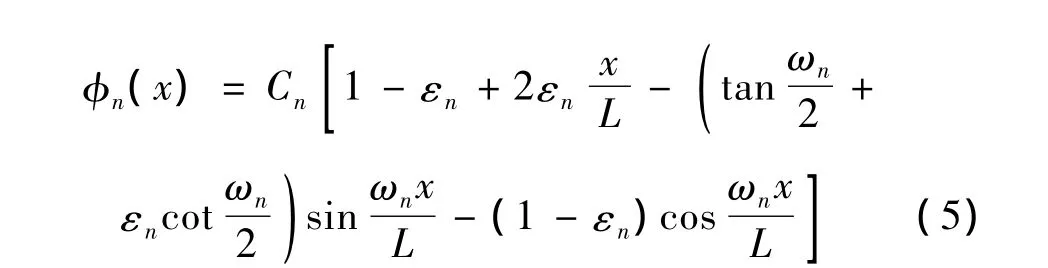
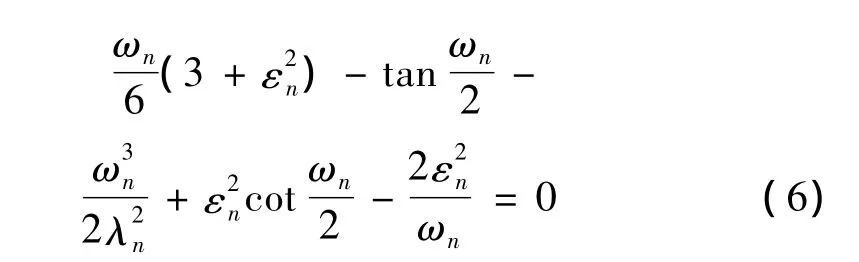
其中λn為材料彈性－幾何參數，考慮到集中質量及高架索傾角的影響［8］，其具體表達式為:

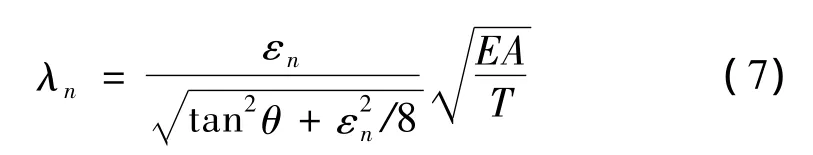
由式(7)可見，高架索系統的材料彈性－幾何參數與集中質量的位置、模態振型因素有關，這也是高架索系統與無集中質量的懸索的重要區別之一。通過上述各表達式可見，集中質量對高架索系統的動力學行為的影響，不僅僅體現在對系統慣性質量的影響，同時還與高架索系統的頻率方程、振型方程中的系數有關，進而影響系統的模態振型和模態頻率，這種強耦合特性，大大增加高架索系統的動力學行為研究的難度。

2 高架索系統面內振動的模態頻率分析

由上述初步分析可見，高架索系統的模態頻率、振型將隨集中質量的在高架索上的位置變化而變化，只有明確了系統模態頻率、振型的變化趨勢，才能更好地為后續的高架索系統的動力學研究的開展鋪平道路，因此，必須首先確定系統模態頻率與集中質量的位置的關系。

由式(5)、式(6)以及式(7)可見系統模態振動的振型及模態頻率是相互關聯的，表達式εn、λn中均含有集中質量在高架索上的位置xm這一基本參數。但是，即使給定xm的值，也無法確定系統振動模態振型及頻率，因此稱xm為局部參數。φn(xm)對應特定集中質量位置的n階模態振型幅值，體現了集中質量對系統質量的貢獻，如果先不考慮 xm的取值，直接給定φn(xm)的值，就可以確定參數εn、λn及高架索系統振動的模態振型和模態頻率，因此稱之為系統的全局參數。

本文通過待定局部參數 xm，而給定全局參數φn(xm)的方式來確定參數 εn、λn，進而由式(5)、式(6)得到高架索系統振動的n階模態頻率ωn及模態振型φn，再由式(5)反過來確定局部參數xm的值。通過改變φn(xm)的值，重復上述步驟，即可以得到高架索系統面內振動的n階模態頻率與集中質量位置的關系，為系統后續的動力學行為研究提供基礎。其中，φn(xm)的取值范圍為(0，1)。借助Mathematica程序，得到了高架索系統的前3階模態頻率與集中質量位置的關系曲線，如圖2所示

圖2 高架索系統的前3階模態頻率與集中質量的位置的關系及各階模態振型(xm=5 m)Fig.2 The first three modal frequencies influenced by the lumped mass of highline cable and modal shapes when xm=5 m

由圖2可見，高架索系統各階模態頻率受集中質量的位置變化的影響很大，當xm≈4 m～6.6 m時，高架索系統的第1、3階模態頻率存在類似滯回非線性的特性，即同一位置對應多個模態頻率、振型。說明集中質量在特定位置時，系統將會存在幾種不同的振動形式。此外，數值分析表明，當xm≈4.5 m ～5.5 m 時，系統的第1、2、3階振動存在1∶1∶2雙重內共振情況;圖2給出了xm=5 m時，系統發生1∶1∶2雙重內共振及1∶2內共振情況的振型圖，后續的數值分析就是針對該情況進行的。本文通過選取不同的第1階模態頻率產生1∶1∶2 雙重內共振及1∶2 內共振情況。系統發生1∶1∶2雙重內共振時，第1階模態振型(O1(r))、3階模態振型(O3(u/r))呈現近似的反對稱特征，第2階模態振型(O2(u/r))為典型的混合(非對稱)模態;而發生1∶2內共振時，系統的第1階模態振型(O1(u))為近似的對稱模態，第2、3階模態振型與雙重共振情況相同。

3 數值分析

參照實際情況，高架索系統的基本參數取值如下:

E=1.8 × 1011Pa;A=4.9 × 10－4m2;ρ≈7800kg/m3;l=50 m;xm=5 m;M=600kg;T=20 kN;f=0.01;θ=π/6。

Ω為高架索的索端激勵頻率，選取Ω=2ω1，為一類典型參激共振情況。下面就針對1∶1∶2雙重內共振(ω3=2ω1≈2ω2)及 1∶2 內共振情況，對高架索系統在平面內的橫向振動的動力學特性進行數值分析。

情況1 1∶2 內共振情況(ω3≈2ω1)

由上述的高架索系統的模態頻率的計算，發生1∶2內共振時系統的各階模態頻率及小參數取值為:ε1=0.0461;ε2=0.0578;ε3=0.1505;ω1=5.3707 rad/s;ω2=6.3252 rad/s; ω3=12.5482 rad/s;

由圖3、圖4可見，對于1∶2內共振情況，高架索系統面內振動以第1階模態振動為主的周期運動;高架索系統的第2、3階模態振動的振幅迅速衰減，與第1、2階模態振動相比，系統的第3階模態振動完全可以忽略不計。

情況2 1∶1∶2 雙重內共振情況(ω3=2ω1≈2ω2)

系統各階頻率及小參數取值為:

ε1=0.0818;ε2=0.0578;ε3=0.1505;ω1=6.2745 rad/s;ω2=6.3252 rad/s;ω3=12.5482 rad/s。

由圖5、圖6可見，對于1∶1∶2雙重內共振情況，高架索系統的振動以前兩階模態振動為主，第2、3階模態振動的振幅比1∶2內共振情況大得多。由于此時系統的前兩階模態振動頻率十分相近，使得系統第1、2、3階模態發生1∶1∶2雙重內共振時，第2階模態也處于近共振狀態，從而導致系統的振動出現第2階模態振幅較大的情況。同時，系統的各階模態振動也不再是簡單的周期運動，高架索系統的第1、2階振動為周期2運動，而第3階振動更為復雜，為周期5運動。

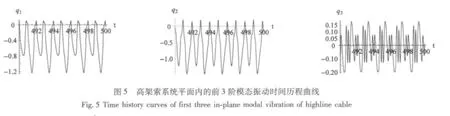
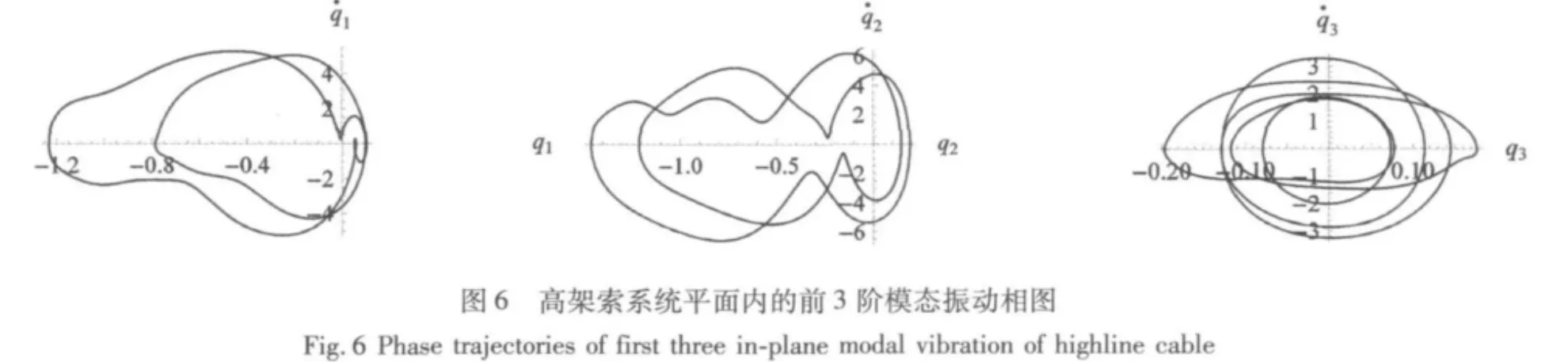
綜上所述，當 xm≈4.5 m ～5.5 m 時，高架索系統將存在1∶1∶2雙重內共振及1∶2內共振兩種振動形式，系統在擾動下可能會在這兩種振動之間跳躍，從而影響到系統的作業效率，甚至導致系統的穩定性。因此，對于該高架索系統而言，在該區間作業時，應盡量保持高架索系統張力及貨物運行速度的恒定，避免在該區域內調節貨物輸送的速度。

4 結論

考慮集中質量在高架索上的位置變化對系統動力學特性的影響，建立了橫向補給系統的高架索面內振動的連續體模型，利用Galerkin方法將連續模型離散為標準的動力學控制方程。引入全局和局部參數的概念，分析了集中質量的位置對系統的前3階模態頻率的影響，得到了他們的關系曲線。對1∶1∶2雙重內共振和1∶2內共振情況下高架索系統的參激振動的動力學行為進行研究，結果表明，高架索系統在發生1∶1∶2雙重內共振時，系統振動的第2、3階振幅值較1∶2內共振情況大得多，且存在復雜的周期2、周期5運動現象。

［1］盧永錦.海上橫向補給高架索道系統數學模型研究［J］.中國造船，1996，37(1):17－22.

［2］余建星，李紅濤.高架索海上補給裝置在小型船舶補給上的應用［J］.海洋技術，2005，24(2):59－62.

［3］嚴梅劍.海上航行橫向補給裝置選型設計［J］.船舶，2004，31(1):51－53.

［4］楊 軍，徐巖山，任愛娣，等.海上補給仿真訓練系統中高架索形態模型研究［J］.海軍工程大學學報，2006，18(4):90－95.

［5］陳自力.集中荷載作用下懸索的面內運動非線性分析與應用［D］.長沙:湖南大學，2006.

［6］Lin H P，Perkins N C.Free vibration of complex cable/mass systems:theory and experiment［J］.Journal of Sound and Vibration，1995，179(1):131－149.

［7］Rega G，Srinil N.Nonlinear hybrid-mode resonant forced oscillations of sagged inclined cables at avoidances［J］.Journal of Computational and Nonlinear Dynamics，2007，2(4):324－336.

［8］Wu Q，Takahashi K，Nakamura S.Formulae for frequencies and modes of in-plane vibrations of small-sag inclined cables［J］.Journal of Sound and Vibration，2005，279(3 － 5):1155－1169.

［9］Irvine H M. Cable structures［M］.Cambridge:The Massachusetts Institute of Technology Press，1981.

［10］Nayfeh A H，Mook D T.Nonlinear oscillations［M］.New York:Wiley-Interscience，1979.

附 錄