船用柴油發電機組非線性隔振系統動態特性分析

高浩鵬，黃映云

(海軍工程大學 船舶與動力學院，武漢 430033)

柴油發電機組作為艦船電站系統的原動力仍在廣泛運用，為艦船的武器系統、導航系統、指揮系統等提供動力源，所以其經常性的使用是必不可少的。柴油機其本身作為一種機械系統，在將化學能轉化為機械能時，其動力傳遞組件的復雜機械運動使得發電機組本身成為船體的一個重要激勵源［1］。考慮到艦船的隱身性，對柴油發電機組安裝隔振系統亦被廣泛使用。目前對非線性隔振系統特性分析大都通過數學模型進行求解［2］，而這種方法主要分析隔振系統自身的特性并且應用于工程實際較為繁瑣，對產生激勵的機械與隔振系統綜合起來分析較少。本文對TBD234V6柴油機發電機組及其線性隔振系統進行多體動力學建模，并通過實驗驗證了模型的正確性;在此基礎上建立了發電機組非線性隔振系統，綜合考慮到激勵源與隔振系統的相互影響，對系統的動態特性進行分析研究。

1 線性隔振系統的建模與實驗驗證

1.1 多體動力學模型的建立

本文對柴油發電機組進行三維實體建模，并通過CAE技術建立機組的多體動力學模型;該模型的多體動力學邊界條件較為復雜［3］，主要包括柴油機發火順序及間隔角、氣缸壓力、各個剛體之間的約束(如圖1所示)、剛體之間的力元等。模型利用柴油機調速器原理合理實現了柴油機啟動工況和穩定工況的模擬，為隔振系統的動態特性分析奠定了基礎。

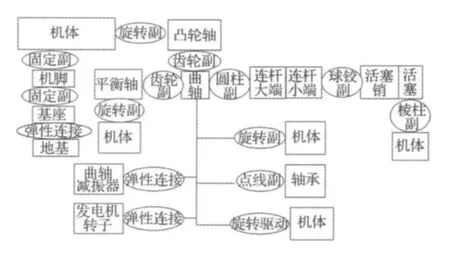
圖1 組件間的約束關系Fig.1 The constrain relation of subassembly

在多體動力學模型建立的基礎上，本文通過襯套力來建立線性隔振系統;為了以便通過實驗驗證模型的正確性，文中隔振器的參數選取與實物EA400隔振器的參數一致，動剛度橫向、縱向、垂向［4］分別為1700 N/mm、5000 N/mm、6500 N/mm，阻尼比取 ζ=0.1。柴油發電機組整機的多體動力學及線性隔振系統模型如圖2所示(為了便于觀察，圖中隱藏了機體以及一些外掛件等)。

圖2 機組及隔振系統實體模型Fig.2 The model of diesel and vibration isolation system

1.2 實驗驗證

柴油發電機組的建模過程相當復雜，然而模型的正確性直接影響計算結果的正確性，所以應對模型的正確性進行實驗驗證。機組零部件眾多，多體系統復雜，運動方式多樣，對單個零件的某個參數來驗證，其可測性與可驗證性是很難保證的。本文選取了柴油機發電機組的振動烈度作為實驗驗證的參數，主要原因有:多體系統模型的建立相對于實際柴油機來講邊界條件簡化了很多，對于高頻信號就較難評價，而振動烈度以速度信號作為參數能較好的反應機組的中低頻段特性，所以模型中易于反映出來;另外振動烈度易于測量并且反映隔振系統的性質。

GJB中評估振動烈度用的是振動速度，而實際的采樣信號為加速度，所以需要采用數值積分方法得到速度信號。文中實驗用的測量儀為杭州億恒科技有限公司生產，型號是AvantLite;加速度傳感器為揚州科動電子有限責任公司生產，型號是KD1005LS的ICP式三向加速度計。作者對多個測點的加速度測量并與計算結果進行對比分析(其中測點1位于柴油機B側自由端機腳附近，測點2在B側輸出端機腳螺栓上，測點3在B1缸缸蓋輸出端側面，測點4在A側自由端機腳附近的機體上，各測點測得的振動速度有效值如表1所示)，發現:多體動力學計算得到三個方向振動速度幅值由大到小依次是橫向、垂向、縱向，這與實驗結果一致;多體動力學計算結果的頻譜圖中對振動速度貢獻量最大的頻率是37.5Hz，這與實驗結果一致;多體動力學計算結果中對結果貢獻量較大的頻率還有25Hz，而實驗結果中這個頻率對振動速度貢獻量較小。對于出現25Hz，作者通過去掉氣缸壓力而利用運動驅動等方法發現，柴油機動力傳遞組件在運動時為變慣量系統，導致模型的動平衡性不是很好，所以多體動力學計算結果中25Hz對振動速度的影響較大。作者列出了額定工況下測點1實測以及對應位置計算得到的垂向速度頻譜圖，如圖3和圖4所示。

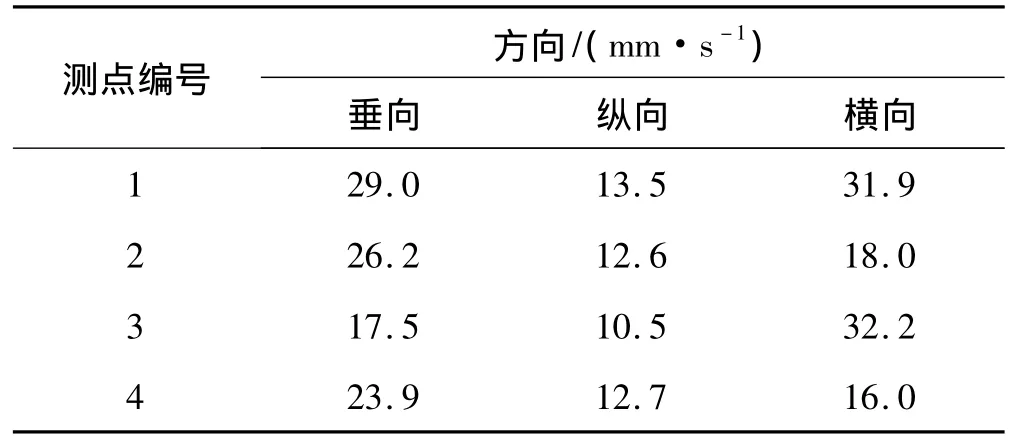
表1 實驗得振動速度值Tab.1 The result of actual measurement vibration velocity

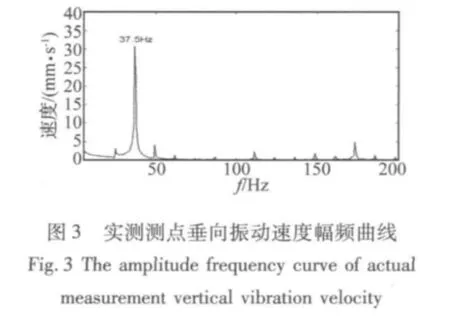
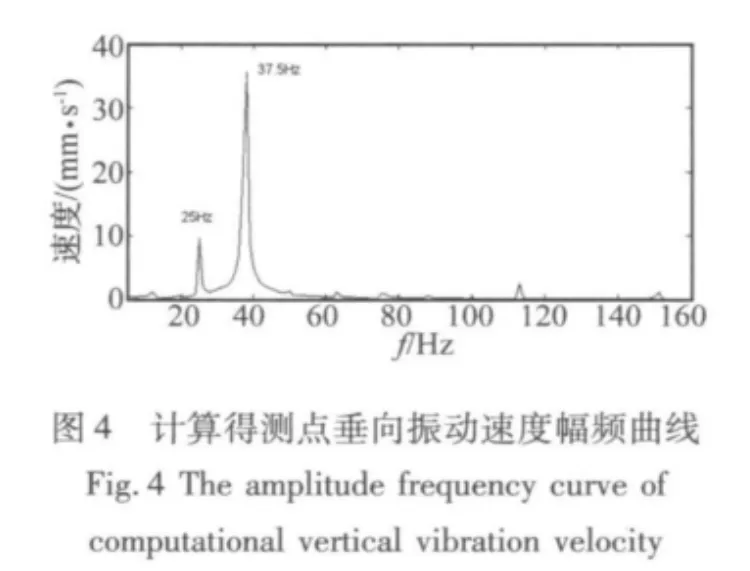
1.3 線性隔振系統特性分析

從隔振器性能的評價角度考慮，傳遞率是其中一個重要評價指標，其主要與系統的自然頻率和激勵頻率有關［5］。對于柴油發電機組來講，其正常工作時轉速為1500 r/min，故其激勵力的頻率主要與動力傳遞組件的一次慣性力與氣缸爆壓有關，即激勵頻率基本為固定值，文中主要對隔振系統的自然頻率進行重點分析。

本文計算的理論基礎是計算多體系統動力學［6］，分析得柴油發電機組對外共有7個自由度(包括機組的6個自由度和動力傳遞組件的1個旋轉自由度)。文中利用多體動力學分析軟件的振動模塊對機組隔振系統性能進行分析;通過掃頻的方式得到系統的固有頻率和振型(如表2所示);另外分析得到動力傳遞組件扭轉自由度的固有頻率為15.1 Hz。由系統的固有頻率、振型、機組的工作基頻(25Hz)以及激勵頻率(37.5Hz)發現，系統繞垂向轉動、垂向平動和繞橫向轉動的頻率都處于非隔振區間，故判斷該隔振器的選型是不合理的。

表2 線性隔振系統的固有頻率和振型Tab.2 Natural frequency and mode shape of linear vibration isolation system

2 非線性隔振系統的建模

通過對線性隔振系統特性分析發現，EA400隔振器對該柴油發電機組的隔振效果不是很好，考慮到氣動隔振器固有頻率低、可靠性高、穩定性好等［7］特點，文中以空氣彈簧為實物，根據氣動隔振器的結構特性，利用三個一維彈簧來模擬空氣彈簧，從而建立非線性隔振系統。文中隔振器的剛度以實驗結果為基礎，通過數據擬合的方式得到剛度與隔振器變形的關系曲線，如圖5和圖6所示;由圖5中可以看出，隔振器壓縮稍大于10 mm的變形開始具有明顯的非線性［8］，這主要是因為氣囊的連接板同囊內的橡膠金屬接觸的這種結構所決定，這種結構在沖擊載荷作用下壓縮時具有很強的抵抗變形的能力。

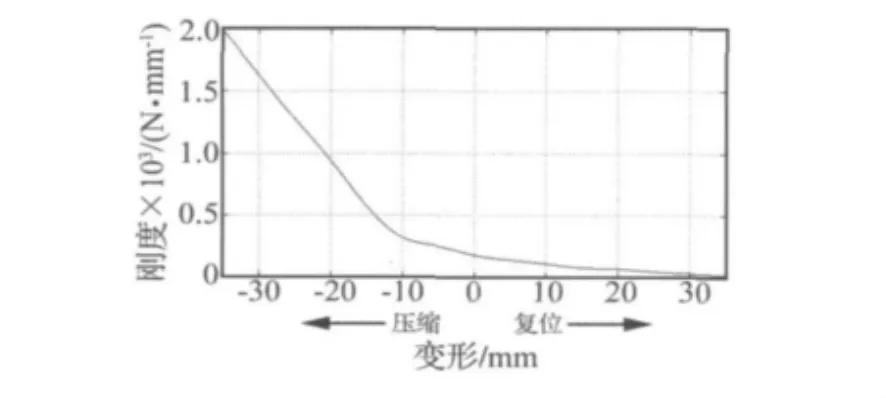
圖5 隔振器垂向動剛度－變形曲線Fig.5 The vertical dynamic stiffness-deformation curve of the vibration isolators

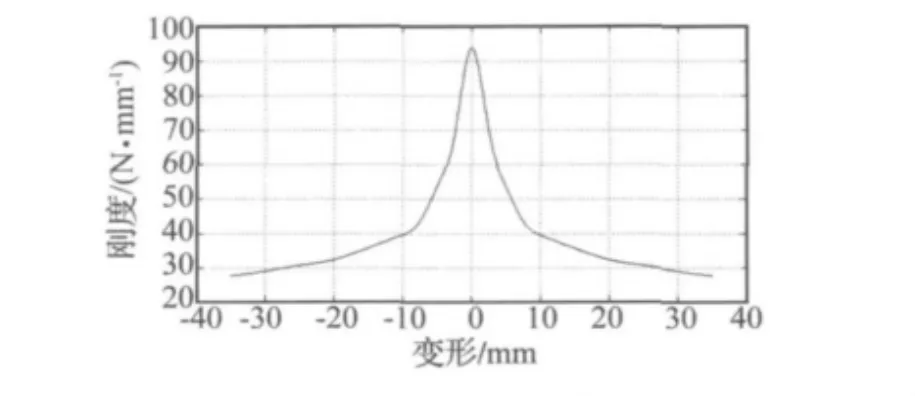
圖6 隔振器縱向動剛度－變形曲線Fig.6 The longitudinal dynamic stiffness-deformation curve of the vibration isolators

由于氣囊隔振器的橫向剛度特別小，故本文在建模時隔振器以30°角傾斜安裝［9］，使得隔振器在柴油發電機組的橫向上也具有較大剛度。在多體動力學軟件分析時，非線性隔振器的模擬是以力與變形的關系來添加的，其力與變形的歷程曲線是通過對實驗得到的剛度與變形的擬合曲線進行數值積分得到。

3 非線性隔振系統的動態特性分析

在非線性隔振系統模型建立的基礎上，作者通過振動模塊對系統的固有頻率及振型進行分析，具體結果見表3;由表中可以發現空氣彈簧的固有頻率較低，遠離柴油機工作的激勵頻率。

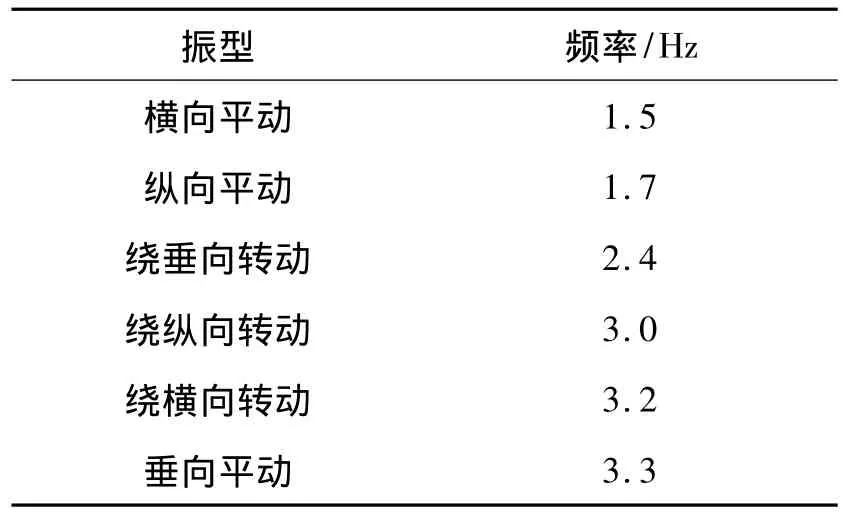
表3 非線性隔振系統的固有頻率和振型Tab.3 Natural frequency and mode shape of non-linear vibration isolation system

3.1 與線性隔振系統的對比分析

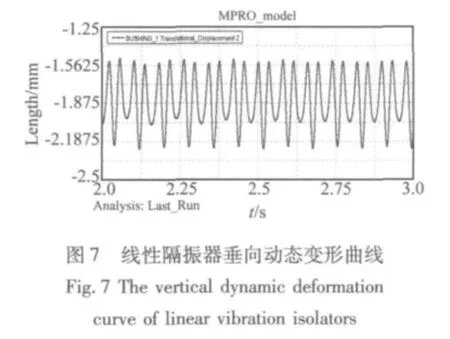
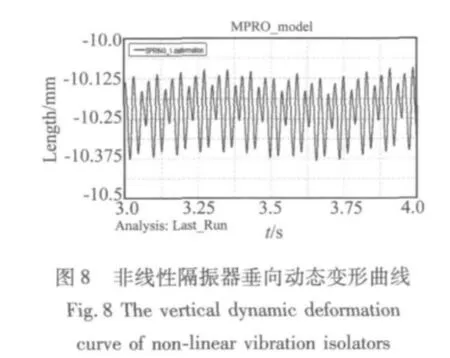
柴油機在啟動過程中由于轉速的變化使得自身激勵的頻率逐漸遞增，在啟動過程中隔振器的變形量較大。柴油發電機組在靜態時，線性隔振器和非線性隔振器的垂向變形分別是1.87 mm和10.23 mm;由于非線性隔振器的剛度值較線性小，故其靜態變形量較大。文中在對非線性隔振器選型時主要使得隔振器動態工作在非線性區域，當柴油機工作在額定工況時(1500 r/min，186 kW)，分別對線性和非線性隔振器的動態變形量(即隔振器變形最大值和最小值之差)進行分析，其數據如表4所示;雖然非線性隔振器的剛度值較線性隔振器小，但由表4可以發現非線性隔振器的橫向和縱向動態變形都小于線性隔振器，說明非線性隔振器的振動傳遞率小于線性隔振器;圖7和圖8為機組額定工況時線性和非線性隔振器垂向變形的時間歷程曲線。作者在對隔振器縱向變形分析時發現，由于機組的重心不在幾何型心處，柴油機工作時在縱向會產生耦合振動。

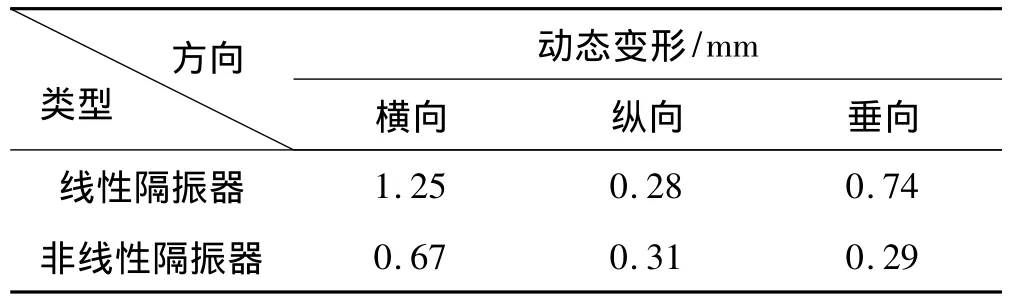
表4 隔振器動態變形Tab.4 The dynamic deformation of vibration is olation

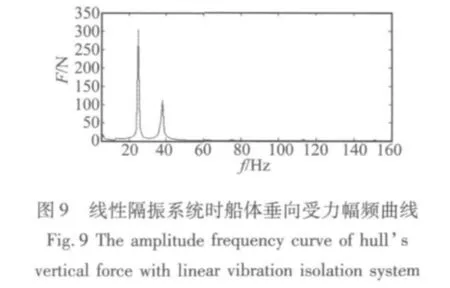
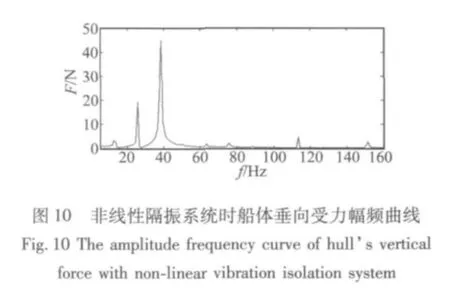
柴油機自身作為振源，對其隔振屬于主動隔振問題;評價主動隔振系統的好壞就是看振源傳遞給基礎力的大小，故本文對線性和非線性隔振系統下柴油機傳遞給船體的力的歷程曲線進行分析，發現柴油機額定工況時傳遞給船體的垂向力的幅值在線性隔振系統和非線性隔振系統下分別為1694 N和282 N。為了進一步分析力的特性，作者對其進行傅里葉變換，線性和非線性隔振系統傳遞給船體垂向力的幅頻特性如圖9和圖10所示。由圖9和圖10對比發現，非線性系統對25 Hz和37.5 Hz的激勵力有很好的隔振作用。另外由圖10中可以發現，在氣缸壓力激勵頻率的1/3、2、3、4次諧頻處都有較明顯的波峰，說明柴油機激勵響應中包括高次諧波、次諧波;圖10中3次諧波的幅值大于2、4次諧波的幅值，即激勵響應的振幅會出現跳躍現象;這兩點特性也是非線性系統區別與線性系統的特點，從反面也論證了非線性隔振系統建模的正確性。

3.2 沖擊條件下非線性隔振系統動態特性分析

當船舶在沖擊條件下為防止船體的振動傳至柴油發電機組的問題屬于被動隔振問題，由于主動隔振與被動隔振的傳遞率在表達式上完全相同，故文中建立的非線性系統較線性系統有良好的被動隔振效果。下面主要建立船舶虛擬沖擊平臺，并分析柴油發電機組工作在額定工況時沖擊條件下的特性。

文中沖擊條件主要模擬船體在受到水下爆炸時的沖擊，根據聯邦德國1985年頒布的BV043/85標準，對船體施加雙重半正弦的沿柴油機橫向加速度沖擊，文中使用的函數為三重IF函數;其中施加沖擊的開始時間是1.6 s;對基礎施加的加速度時域曲線如圖11所示，圖中的毛刺是由于軟件分析的精度以及IF函數本身易導致跳變。

圖11 虛擬沖擊加速度曲線Fig.11 The emulational impact curve of acceleration

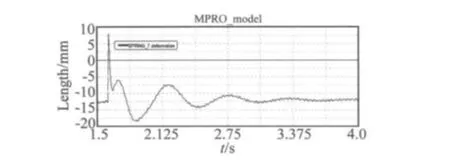
圖12 沖擊條件下非線性隔振器橫向動態變形曲線Fig.12 The transverse dynamic deformation curve of non-linear vibration isolators under impact loads

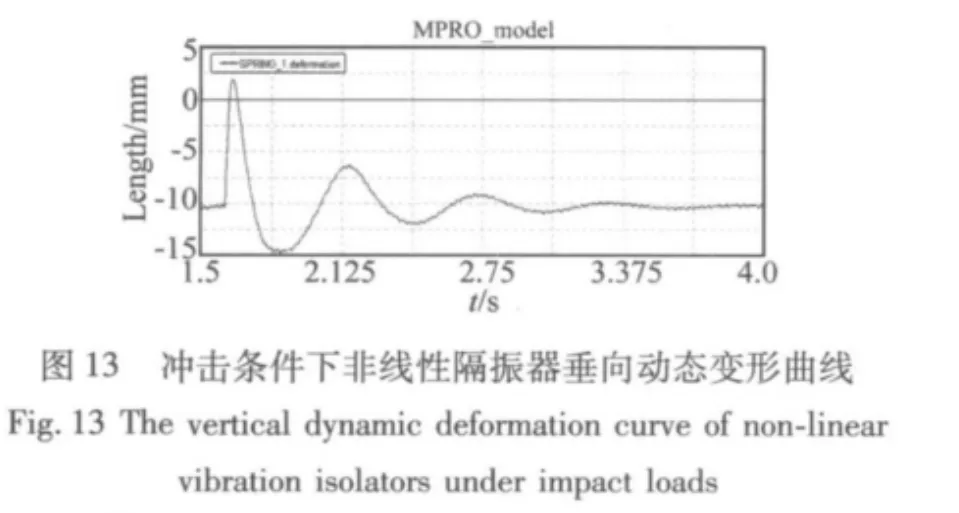
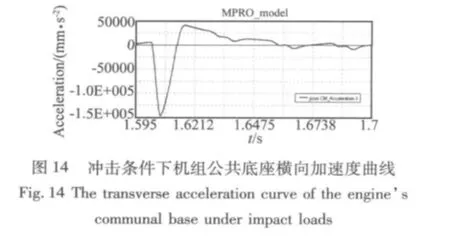
圖12是柴油發電機組額定工況時隔振器橫向變形曲線，由圖中發現在沖擊峰值時刻隔振器變形瞬間產生大的跳躍，在恢復穩定狀態時又遇到柴油機動不平衡的一次慣性力，可見在沖擊條件下隔振器橫向變形較大，特別是機組上端的一些與船體有連接的外掛件(如煙囪)，故在空間位置允許的情況下應在柴油發電機組的上端部位安裝限制橫向位移的氣動減振器。圖13是耦合作用下隔振器垂向變形曲線，由于阻尼設置較小其衰減時間較長，在衰減過程中由于隔振器非線性因素其峰峰值對應的時間差不相等。圖14是柴油發電機組公共底座的橫向加速度時間歷程曲線，其幅值約是雙重半正弦波幅值的1/10，表明氣動隔振器有良好的隔振效果。

4 結論

本文主要建立了柴油發電機組多體動力學以及線性隔振系統模型，并通過實驗驗證了模型的正確性;在此基礎上構建了非線性隔振系統模型，分析了非線性隔振系統在柴油機正常工作時的動態特性，并與線性隔振系統特性進行對比;另外構建了船舶沖擊條件下的虛擬模型，并對沖擊條件下非線性隔振系統的動態特性進行分析;結果表明非線性隔振系統較線性隔振系統有良好的隔振效果，特別是當船舶受到瞬時高強度脈沖激勵時強非線性隔振系統的被動隔振效果較好。

柴油發電機組是船舶噪聲的一個主要激勵源，要對其隔振系統特性分析就首先對機組進行正確的建模，文中運用計算多體動力學方法對整個柴油機的運動機構進行系統建模，在論證模型正確性的基礎上以氣動減振器為實物建立非線性隔振系統并對其進行動態分析，分析結果較為可靠。文中的建模以及分析過程可應用于船舶其它機械設備，工程上可以簡單實現船舶隔振系統的選型和參數優化。另外文中建立的船舶沖擊條件下的虛擬模型為船舶各種機械設備甚至電子設備的抗沖擊研究提供了一定的基礎。多體動力學中非線性隔振系統可以簡單的實現參數化設計與控制，與MATLAB等數值計算軟件相結合，若能在工程運用上實現混沌控制，就可以更好的改善隔振系統的性能，具有重要的應用價值。

［1］朱孟華.船舶內燃機動力學［M］.北京:國防工業出版社，1979.

［2］黃映云，吳善躍，朱石堅.囊式空氣彈簧隔振器的特性計算研究［J］.振動工程學報，2004，17(2):249 －252.

［3］高浩鵬，黃映云，王雪山.船用柴油機運動機構動力學動態分析方法研究［J］.振動與沖擊，2009，28(8):84 －87，200.

［4］何 琳，束立紅，王 強.艦船用隔振器系列型譜［M］.北京:中國人民解放軍海軍裝備部，2005.

［5］師漢民.機械振動系統分析·測試·建模·對策［M］.武漢:華中科技大學出版社，2004.

［6］張國慶，黃伯超，浦狄強，等.汽車發動機曲軸系動態仿真［J］.系統仿真學報，2006(8):2293 －2295.

［7］Ravindra B，Mallik A K.Performance of non-linear vibration isolators under harmonic excitation［J］.Journal of Sound and Vibration，1994，170(3):325 －337.

［8］朱石堅，何 琳.船舶減振降噪技術與工程設計［M］.北京:科學出版社，2002.

［9］陳志敏，黃映云，彭 敏，等.基于ADAMS的船舶隔振系統性能研究［J］.振動與沖擊，2007，26(8):101 －103.