屏蔽電纜轉移阻抗時域測量方法研究

張 琦 石立華 周穎慧 邵志學

(解放軍理工大學工程兵工程學院，江蘇 南京 210007)

1． 引 言

屏蔽電纜廣泛應用在各類場合。由于屏蔽結構、屏蔽材質的不同，在屏蔽效能上也存在著較大差異。反映電纜屏蔽層屏蔽效能本質的是電纜特征參數轉移阻抗，以往對電纜屏蔽效能的評價主要通過轉移阻抗的測量來實現。目前，對屏蔽電纜表面轉移阻抗的測量方法主要有線注入法[1-2]和三同軸法[3-6]兩大類。國內外已有不少學者對其進行試驗與理論上的研究[7]。國內標準GB9023-1988[8]和國際標準IEC62153-4-3-2002[9]、EN50289-1-6-2002[10]給出了轉移阻抗的明確定義，如圖1所示。

圖1 轉移阻抗的定義

轉移阻抗的定義形式為

(1)

式中：I0是電纜屏蔽層上流過的電流； dU/dz是電纜屏蔽層與電纜芯線所組成的傳輸線上單位長度的電壓降；I是電纜芯線上流過的電流。

以往轉移阻抗的測量主要是在頻域內進行的，即用網絡分析儀對屏蔽電纜S參數進行測量，換算得到ZT(ω)曲線。而在一些場合需要直接評價電纜對電磁脈沖的屏蔽效果，頻域測試曲線不能直觀反映這一效果。周啟明等人曾采用電磁脈沖直接注入的方法，測量了某多芯屏蔽電纜的屏蔽效果[11]。但是時域測量屏蔽效能與頻域測量的互換方法，以往尚未有討論。

本文針對屏蔽電纜表面轉移阻抗時域測試需求，提出具體的實現方法，建立了時域測試系統；并與頻域測試結果進行對比；研究了測試數據的建模方法，建立了轉移阻抗的時域描述模型，為屏蔽電纜的屏蔽性能表征提供了新的參數模型。

2． 轉移阻抗時域測試系統

2.1 測試系統設置

依據轉移阻抗的測試標準，轉移阻抗測試系統主要由高壓脈沖源、三同軸裝置、阻抗匹配網絡、數字存儲示波器、同軸衰減器以及受試件電纜等組成，測試系統構成如圖2所示。圖2中，三同軸測試裝置適應頻率范圍為30 MHz以下時，樣品長度為1 m；適應頻率范圍為100 MHz以下時，樣品長度為0.3 m.如果最高測試頻率為fmax(Hz)，則允許的最大耦合長度[3]Lc,max為

圖2 轉移阻抗時域測試系統圖

(2)

式中，εr1為電纜相對介電常數。

該測試系統中三同軸裝置有效耦合長度為0.3 m，實際長度為0.45 m，屏蔽套管外徑為51 mm，內徑為48 mm，管厚為3 mm.其測試原理為：高壓脈沖源注入信號至三同軸測量系統的內電路，數字存儲示波器同步監測外電路耦合的電壓信號。同時，示波器同步接收了高壓脈沖源注入的源信號。測試系統實際將電流注入至屏蔽電纜芯線，測量屏蔽電纜屏蔽層的耦合電壓。由此可以從示波器得到注入內電路的電流波形數據和外電路耦合的電壓波形數據，進而評價表面轉移阻抗。

2.2 高壓脈沖源選擇

高壓脈沖源作為屏蔽電纜轉移阻抗測試系統的信號源設備，其輸出波形的性能直接影響著測試系統的測量精度。測試系統能夠測試不同屏蔽效能的電纜，要求測量信號具有較大的電壓輸出動態范圍，考慮到示波器的最小接收電壓為2 mV，脈沖源輸出電壓峰值至少應為200 V；同時，轉移阻抗作為描述屏蔽電纜效能的本征參數，要求注入信號具有較寬的頻譜。

本文采用的高壓脈沖源[12]輸出雙指數脈沖波0～6 kV可調，上升沿時間2～3 ns，半寬度25 ns，輸出阻抗50 Ω，具有同步10倍衰減輸出端口，并附加方波發生器功能。輸出的雙指數脈沖波和方波均達到美軍標準MIL-STD-461E[13]的指標要求。輸出的典型脈沖波形及其頻譜如圖3、圖4所示。

2.3 匹配負載與網絡

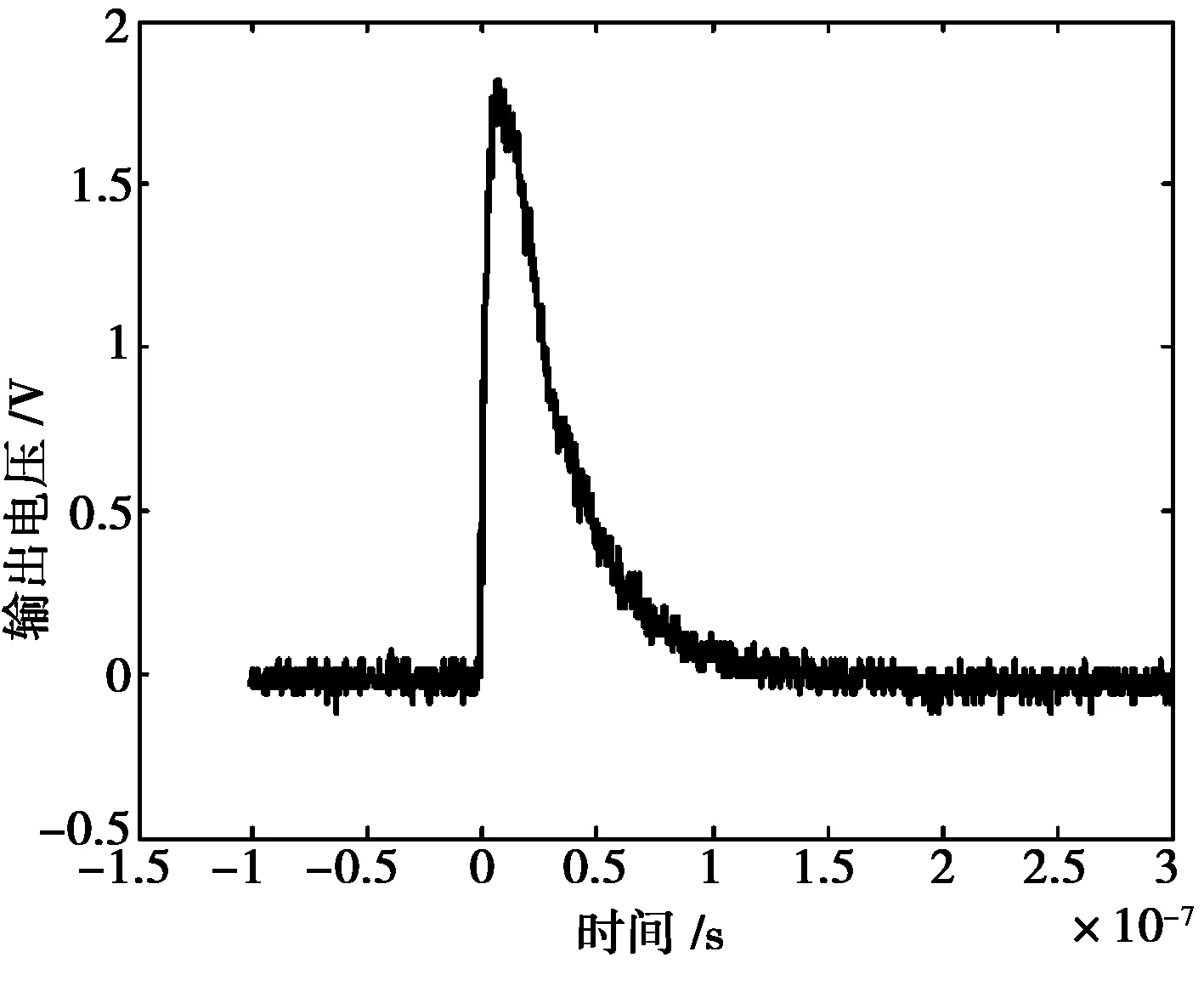
圖3 高壓脈沖源輸出的典型脈沖波形

圖4 高壓脈沖源輸出的典型脈沖波形頻譜

測試系統內電路的輸入和外電路的輸出均要求匹配，達到50 Ω輸入輸出的標準。為保證負載匹配，圖2中R1取值與內電路的特性阻抗Z1相等，R2取值與外電路的特性阻抗Z2相等。對于外屏蔽管取不同直徑以及不同尺寸電纜的情況下，R2的取值可按以下兩式計算[3]。

R2=1.4×Zout-50

(3)

(4)

式中：Dout為外層屏蔽銅管的內徑，單位：mm；Din為電纜屏蔽層的外徑，單位：mm.

內、外電路匹配負載的精確計算是非常重要的。內電路不匹配易形成反射，電流不能有效注入；外電路不匹配，測試系統得不到最大的耦合電壓，均影響測量精度。如圖2所示，該系統外電路的匹配負載設置在三同軸套筒的外面，可以更方便地調節負載大小，達到精確匹配的目的。當然，匹配負載設置在三同軸套筒外，必須要和匹配網絡一樣做好屏蔽，否則會影響測量精度。

以外電路匹配設計為例，若特性阻抗小于50 Ω，則匹配電路的連接方式如圖5所示。圖5中U2為外電路耦合電壓，Uosc2為示波器測量值，R2為外電路匹配負載，RS、RP取值分別為

(5)

(6)

則匹配網絡的增益系數為

(7)

若特性阻抗大于50 Ω，則匹配電路的連接方式如圖6所示。圖6中U2為外電路耦合電壓，Uosc2為示波器測量值，R2為外電路匹配負載，RS、RP分別為

(8)

(9)

圖5 特性阻抗小于50 Ω時的匹配電路

圖6 特性阻抗大于50 Ω時的匹配電路

則匹配網絡的增益系數為

(10)

由以上方法可以得到SYV-50-3型同軸電纜轉移阻抗測試的相關數據為：R1=50 Ω，R2=183 Ω，RS=156 Ω，RP=59 Ω，K=0.5398。

測量系統采用LecroyWavRunner 6100A示波器作為信號接收機，其模擬帶寬為1 GHz，最高采樣速率為5 GHz，數據記錄長度最高為1 M，可嵌入用戶自定義數據處理功能。屏蔽電纜轉移阻抗時域測試系統實物如圖7所示。

圖7 轉移阻抗時域測試系統

3． 測試數據處理

測試得到系統注入電壓Uosc1波形如圖3所示，SYV-50-3型同軸電纜和SYV-50-5型同軸電纜耦合電壓Uosc2波形，分別如圖8、圖9所示。

圖8 SYV-50-3型同軸電纜耦合電壓波形圖

圖9 SYV-50-5型同軸電纜耦合電壓波形圖

3.1 直接評價電纜的屏蔽效能

這是時域測試系統的一個最直接的應用。主要目的是評價特定長度的電纜對特定脈沖的屏蔽性能的好壞。首先，由示波器獲取的數據計算注入電流I1和耦合電流I2，分別為

(11)

(12)

式中：M為高壓衰減倍數，取值1000；K為匹配網絡增益系數。

其次，計算電纜峰值屏蔽效能，計算公式為

(13)

式中：SEP為峰值屏蔽效能，單位：dB；I1,P為注入電流峰值；I2,P為耦合電流峰值。

以SYV-50-3型和SYV-50-5型同軸電纜為例，對圖3所示雙指數波脈沖峰值屏蔽效能分別為78.5980 dB和95.1380 dB.

同時，還可以觀察電纜屏蔽效能曲線。分別對I1和I2做快速傅立葉變換，得到I1(jω)和I2(jω)，則電纜屏蔽效能計算公式為

(14)

式中，SE為屏蔽效能，單位：dB.

SYV-50-3型和SYV-50-5型同軸電纜的屏蔽效能曲線如圖10所示。

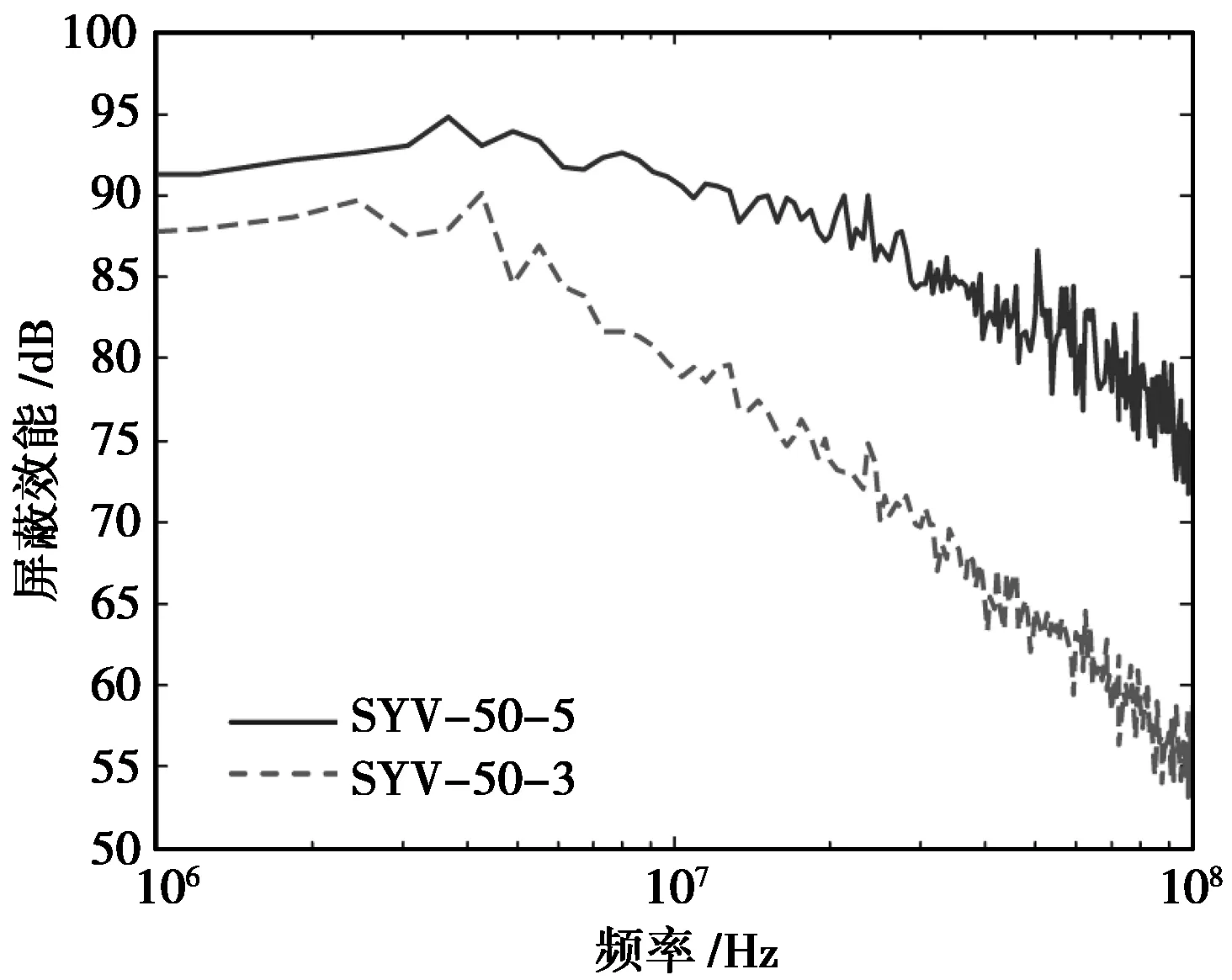
圖10 同軸電纜屏蔽效能曲線

3.2 計算電纜轉移阻抗ZT

由于轉移阻抗是在頻域下定義的，分別對I1和U2做快速傅立葉變換，得到I1(jω)和U2(jω)。則轉移阻抗為

(15)

式中，L為有效耦合長度，取值0.3 m.

從而得到了轉移阻抗曲線，如圖11、圖12所示。

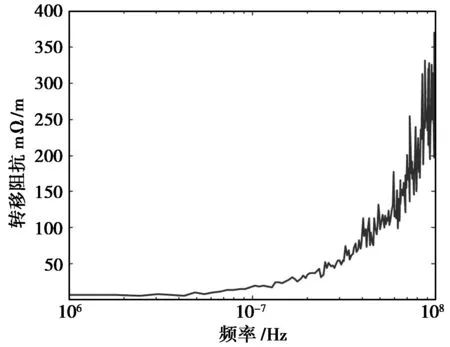
圖11 SYV-50-3型同軸電纜轉移阻抗

圖12 SYV-50-5型同軸電纜轉移阻抗

3.3 計算數據驗證

為了驗證時域測試系統的可靠性，使用Agilent 34401A多功能表直接測量電纜屏蔽層的直流阻抗，約在7～13 mΩ左右。此數據包含測量時的接觸阻抗，具有一定的不確定性，但與轉移阻抗時域測量曲線低頻數據在同一數量級上，低頻數據基本吻合。同時，使用Agilent 4396B網絡分析儀進行頻域測試，得到插入損耗

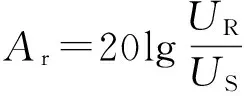
(16)

式中：Ar為插入損耗，單位dB；UR為網絡分析儀耦合電壓；US為網絡分析儀注入電壓。

將其轉換為轉移阻抗，計算公式為

(17)

式中：K為匹配網絡增益系數；L為有效耦合長度。

從而得到頻域測試下的轉移阻抗曲線，與時域測試結果進行對比，兩者基本吻合，如圖13所示。

圖13 SYV-50-3型同軸電纜轉移阻抗時域與頻域測試曲線

4． 轉移阻抗參數化建模

圖13中時域測試獲得的表面轉移阻抗曲線在高頻段有較大噪聲，是由于求取輸入輸出間傳遞函數時采用了式(15)，在高頻段信號受到噪聲干擾，而除法運算放大了這一噪聲，下面將討論采用參數化模型去除這一影響。

4.1 選擇參數化模型

由于屏蔽電纜是一個無源線性網絡，轉移阻抗可以作為一個線性系統的頻率響應特性來分析[14-16]。根據信號與系統的基本原理，一個線性時不變(LTI)離散系統在時域中可以用線性常系數差分方程來表述為

(18)

由上式的Z變換得到

(19)

式中：H(z)為傳遞函數模型；M，N為模型階數；a，b為模型參數；n，r，z-1為時間延遲。

因此，可以根據實測數據y(n)和x(n)，為轉移阻抗建立一個形式為式(19)的傳遞函數計算模型，該模型的參數化譜將有效抑制噪聲的影響，同時便于在時域分析計算中應用[17]。

4.2 模型參數估計

參數估計要求使辨識出來的模型與實際的傳遞過程在某種意義上是最接近的。最小二乘法是一種在工程實踐中應用最早和最廣泛的基本方法，它依據的準則是模型輸出與實際輸出之間的誤差平方和最小[18-19]。

考慮誤差ε(n)的影響，將式(19)改寫為

y(n)=-a1y(n-1)-…-aNy(n-N)+

b0u(n)+b1u(n-1)+…+

bMu(n-M)+ε(n)

(20)

針對輸入數據時間序列為t=1,2,3,…,Nt的情況，寫成矩陣形式

YN=HNθ+εN

(21)

式中：YN=[Y(1),Y(2),…,Y(Nt)]T

(22)

εN=[ε(1),ε(2),…,ε(Nt)]T

(23)

(24)

θ=[a1,a2,…,aN,b0,b1,…,bM]T

(25)

θ即為待估計的模型參數。根據參數估計的最小二乘法，設定目標誤差函數為

(26)

則參數向量θ的最小二乘估計值為

(27)

以SYV-50-3型同軸電纜為例，它的參數化辨識結果如表1所示。

表1 SYV-50-3電纜轉移阻抗模型參數辨識結果

則該屏蔽電纜轉移阻抗傳遞函數為

(28)

圖14(看824頁)是利用式(28)對屏蔽電纜的電磁脈沖響應進行估計的結果，可見實際輸出與建模輸出十分相近，3階模型可獲得足夠的建模精度。 模型參數化譜與時域測量轉移阻抗曲線的對比效果如圖15(看824頁)所示。由此可見，參數化譜比較平滑，模型有效抑制了高頻噪聲。更為重要的是，式(28)形式的模型，簡潔而完整地體現了屏蔽層表面轉移阻抗的全部信息，與以往采用ZT(ω)曲線的表征方法相比，大大減少了數據量；同時，利用該模型估計屏蔽電纜芯線的響應，可直接采用式(19)形式的時域濾波算法，能夠簡化運算量。

4.3 模型有效性進一步驗證

表1的模型參數是在前沿2.3 ns、半脈寬25 ns的雙指數波條件下獲得的。下面，將進一步驗證該模型對其他輸入波形響應估計的有效性。首先，采用前沿2 ns、脈寬100 ns的方波對SYV-50-3型同軸電纜進行測試，輸入波形如圖16所示。

采用表1的參數估計芯線耦合電壓，并與實測輸出波形對比，效果如圖17(看824頁)所示，兩者的波形是吻合的。

此外，還對前沿5 ns、半脈寬100 ns的雙指數波進行測試與估計，實測輸出波形與建模估計波形也是吻合的。輸入波形如圖18所示，估計效果如圖19(看824頁)所示。

圖16 輸入的方波波形

圖18 輸入的雙指數波形

5． 結 論

本文提出了屏蔽電纜轉移阻抗時域測試方法，建立了測試系統。時域測試不僅能夠直觀、形象反映電纜電磁脈沖的耦合情況，還能夠換算獲得表面轉移阻抗曲線。在此基礎上，提出了屏蔽電纜轉移阻抗參數化建模方法，不僅可以獲得更為清晰的轉移阻抗曲線，更為重要的是，這一參數化模型是對ZT(ω)的一種更為簡潔的表述，在場-線耦合分析中用于替代ZT(jω)，將大大提高計算效率。

[1] LEE H Y, OH H S, PARK D C. Measurement of transfer impedance of shielded multiconductor telecommunication cables using IEC 96-1 line injection method[C]//Proceedings of the IEEE International Symposium on EMC, 2003, 3: 1012-1015.

[2] KOROVKIN N, NITSCH J, SCHEIBE H J. Improvement of cable transfer impedance measurement with the aid of the current line method[C]∥ Proceedings of the IEEE International Symposium on EMC, 2003: 1148-1151.

[3] 朱榮華, 李謙若. 表面轉移阻抗的測量-三同軸方法[J]. 光纖與電纜及其應用技術, 2005, 39(4): 8-11.

ZHOU Ronghua, Li Qianruo. Measurement of surface transfer impedance-triaxial method[J]. Optical Fiber Electric Cable, 2005, 39(4): 8-11. (in Chinese)

[4] ORLANDI A. Frequency and time domain modeling of the transfer impedance and distributed longitudinal induced voltage by means of a spice equivalent circuit[J]. IEEE Trans. Electron. Comput., 2003, 45(1): 125-129.

[5] MORRIELLO A, BENSON T M, DUFFY A P, et al. Surface transfer impedance measurement: a comparison between current probe and pull-on braid methods for coaxial cables[J]. IEEE Trans. Electron. Comput., 1998, 40(1): 69-76.

[6] 雷 震, 蔣全興. 基于遺傳算法的轉移阻抗測試裝置優化設計[J] .電波科學學報, 2007, 22(1): 69-72.

LEI Zhen, JIANG Quanxing. Optimization design of transfer impedance testing device[J]. Chinese Journal of Radio Science, 2007, 22(1): 69-72. (in Chinese)

[7] 齊 磊, 崔 翔, 谷雪松. 屏蔽電纜轉移阻抗和轉移導納的寬頻測量[J] .電波科學學報, 2007, 22(4): 696-701.

QI Lei, CUI Xiang, GU Xuesong. Wide-frequency measurement of transfer impedance and transfer admittance of shielded cable[J]. Chinese Journal of Radio Science, 2007, 22(4): 696-701. (in Chinese)

[8] GB 9023. 射頻同軸電纜屏蔽效率的測量方法(轉移阻抗)[S]. 1988.

GB 9023. Methods of Measurement of Screening Efficiency for Radio Frequency Coaxial Cables-Test Method for Transfer Impedance[S]. 1988.

[9] IEC62153-4-3. Metallic Communication Cabletestmethods Part4-3: Electromagnetic Compatib-ility(EMC)Surfacetransfer Mpedancetriaxialmethod[S]. 2002.

[10] EN50289-1-6. Communication Cables Specification for Test Methods Part 1-6: Electrical Test Methods Electromagnetic Performance[S]. 2002.

[11] 周啟明, 鄧建紅, 李小偉, 等. 脈沖電流注入法求多芯電纜的傳輸函數[J].信息與電子工程, 2006, 4(4): 254-257.

ZHOU Qiming, DENG Jianhong, LI Xiaowei, et al. Research of transfer function for multi-core cable by injecting method of current[J]. Information and Electronic Engineering, 2006, 4(4): 254-257. (in Chinese)

[12] 譚堅文, 石立華, 李炎新, 等. 快前沿高壓脈沖源的開發及實驗研究[J].強激光與粒子束, 2004, 16(11): 1434-1436.

TAN Jianwen, SHI Lihua, LI Yanxin, et al. Development and experimental research on the fast rise time EMP generator[J]. High Power Laser and Particle Beams, 2004, 16(11): 1434-1436. (in Chinese)

[13] MIL-STD-461E: Requirements for the Control of Electromagnetic Interference Characteristics of Subsystems and Equipment[S]. 1999.

[14] HANIQUE E. A transfer function is a reliable tool for comparison of ful-and chopped lightning impulse tests[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1261-1266.

[15]MALEWSKI R, POULIN B. Impulse testing of power transformers using the transfer function method[J]. IEEE Transactions on Power Delivery, 1988, 3(2): 476-489.

[16] 石立華, 周璧華. 自積分式脈沖磁場傳感器的補償研究[J]. 電波科學學報, 1995, 10(4): 50-55.

SHI Lihua, ZHOU Bihua. A compensation of the self integrating magnitic field sensor[J]. Chinese Journal of Radio Science, 1995, 10(4): 50-55. (in Chinese)

[17] ZHOU Yinghui, SHI Lihua, GAO Cheng, et al. Combination of FDTD with digital filter in analyzing the field-to-transmission line coupling[J]. IEEE Trans. on EMC, 2008, 50(4): 1003-1007.

[18] ORAIZI H. Application of the method of least squares to electromagnetic engineering problems[J]. IEEE Antennas and Propag., 2006, 48(1): 50-74.

[19] ORAIZI H. Solution of the junction of TE11-mode circular waveguides by the method of least squares[J]. International Journal of Engineering Sciences, 2004, 15(3): 25-39.