甚低頻在多模干涉區的場強起伏標準偏差估計

張世田 陳恩平 王元新 潘威炎 張紅旗

(中國電波傳播研究所，山東 青島 266071)

1. 引 言

甚低頻(VLF)波是指頻率范圍為3～30 kHz的電磁波，其工作波長為100～10 km，地面與電離層對此頻段的電磁波具有良好的反射特性，電波在地面與電離層之間來回反射導引傳播，從而構成地—電離層波導[1-2]。由于VLF波傳播損耗小、信號穩定、且能夠滲透一定深度的海水從而在海軍通信與導航中有重要應用。

VLF在地-電離層波導中有多個傳播波模，每個傳播波型都有各自的傳播相速、衰減率、激勵因子等，接收點的信號場強是各個傳播波型疊加的結果。在各個傳播波模中，TM0波模的衰減率最低，稱作為基模。在幾千千米以外，高階波模已衰減至不起作用，稱作單模區。在中近區因為多個波模同時存在，各個波模的傳播相位不盡一致，故出現“干涉”現象，稱之謂“多模干涉區”。

由于電離層的狀態不是固定不變的，對于固定接收點而言，信號的幅度與相位亦是有變化的，除了隨季節、晝夜的規則變化外，還有隨機的不規則變化。傳播相位隨機起伏標準偏差對于VLF導航系統而言，是影響導航定位精度的重要參數，而信號場強起伏的標準偏差則是估計VLF通信可靠度的重要參數。

美國學者Watt根據10～20 kHz范圍內的各種測試結果, 在文獻[3]給出大距離條件下(單模區)傳播相位起伏標準偏差的一個經驗公式，同時給出了相應場強起伏偏差的估計。但此二經驗公式僅適用于單模區，對于多模區特別是場強極小點附近不適用。文獻[4]給出了多模區VLF傳播相位起伏標準偏差的估計公式，此公式在單模區自動地轉化為美國學者給出的公式，在多模區與我國的實測結果吻合的相當好。但迄今為止，多模區VLF場強起伏標準偏差的估計尚未有較好的方法。本文將對此深入分析研究。

2. 多模干涉區內的場強和傳播相位的空間變化

依據VLF波導的傳播理論[5]對于地基的發射天線而言，它產生的VLF電場垂直分量可表示為

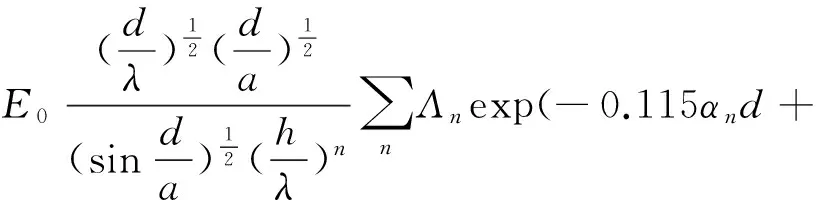
(1)

式中：

(2)

p是輻射功率以kW計；d是收發點之間大圓距離以km計；a是地球半徑6370 km；h是電離層高度；λ是自由空間波長；Λn,αn,υn分別為第n階模的激勵因子、哀減率和相速。若記第n階模的相對幅度和相位分別為Fn和φn，則有

Fn=|Λn|exp(-0.115αnd)

(3)

(4)

當考慮到沿傳播路徑上，由于傳播條件的變化，各階模的參數可能不均勻，則

(5)

(6)

此時總的電場可表示為

(7)

總場的幅度可表示為

(8)

式中M為幅度干涉因子，表示高階模對總場幅度的影響。

(9)

根據文獻[6]場強隨距離變化的表達式，文獻[7]提供的地面電磁參數可計算白天沿傳播路徑上場強的幅度，并與文獻[8]的實測數據進行了比較，如圖1所示。

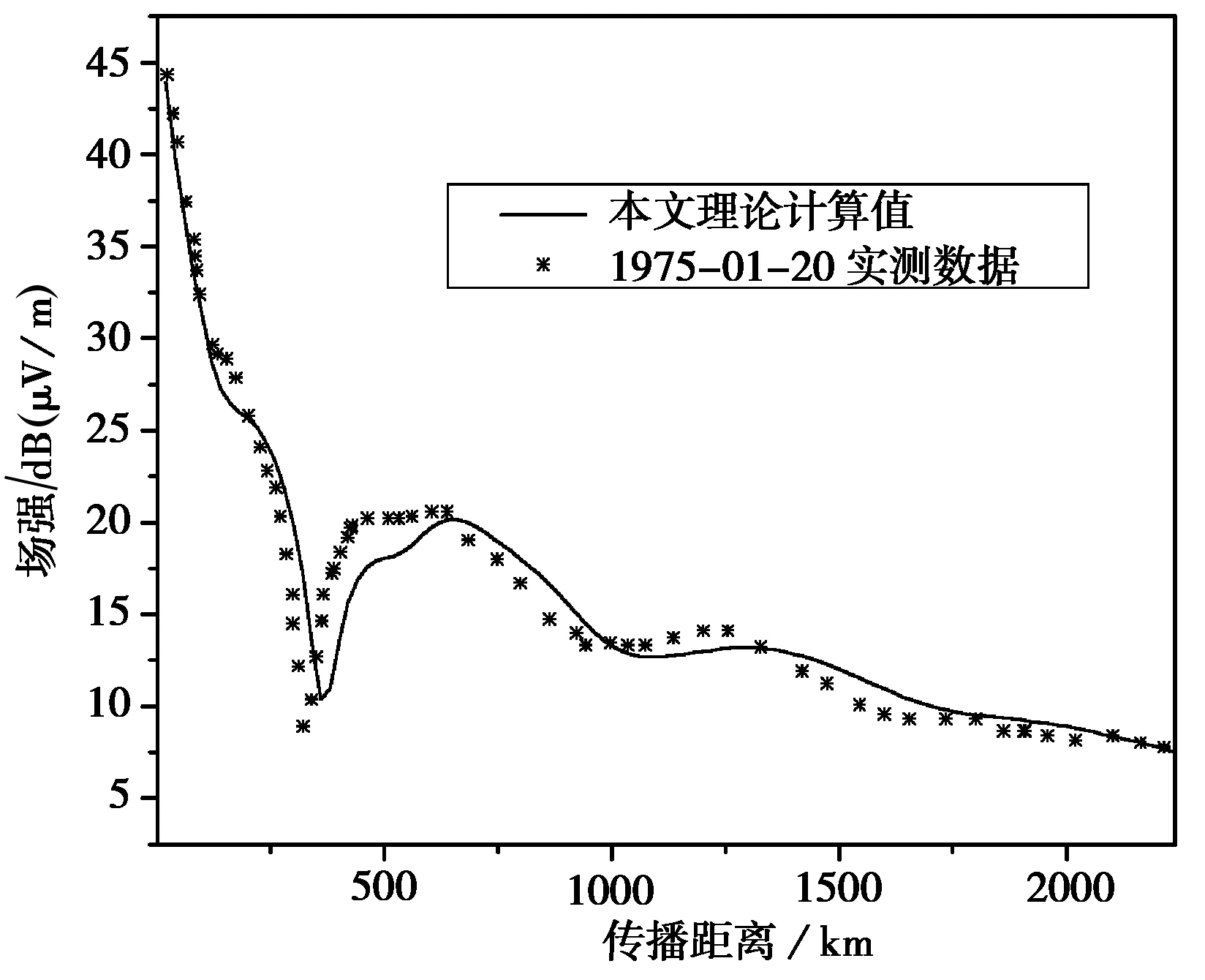
圖1 場強隨傳播距離的變化(大同至海口)

由圖1可見理論計算值與實測值能夠較好的吻合，這也說明了傳播路徑上各階模的傳播參數計算值是準確的。

3. 引起信號幅度和相位隨機起伏的理想化

根據文獻[5]將電離層隨機變換引起的VLF幅度和相位的隨機變化理想化為沿傳播路徑的等效反射高度的隨機變化所致，即認為沿傳播路徑上的電離層等效反射高度可以表示為

h(d,t)=h0(d)+δh(d,t)

(10)

式中：h(d，t)表示傳播路徑上某地在時刻t的電離層等效反射高度；h0(d)是該地點電離層反射高度的期望值； δh(d,t)是它的隨機變化部分，它的期望值應為0.即

E(δh(d,t))=0

(11)

電離層等效反射高度隨機起伏引起的各個模式的相位和相對幅度的隨機變化可由式(3)和(4)求出，它們是

(12)

(13)

dαn/dh和dυn/dh分別代表第n階模衰減率和相速對于電離層等效反射高度的導數，可由波導理論計算出來。從式(12)和(13)可以看出，各階模的幅度與相位亦有相應的隨機變化，它們與電離層等效反射高度隨機起伏有關的隨機變化量dξ成正比，其中

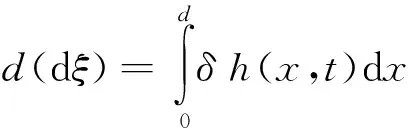
(14)

4. 信號幅度隨機起伏標準偏差的估計

由式(8)可得，當沿傳播路徑上，電離層等效反射高度有隨機起伏變化時，接收點信號幅度應有相應的隨機變化，可以表示為

(15)

(16)

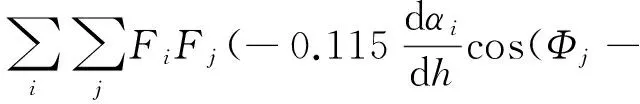
(17)

函數G(d)、M(d)等都是僅與接收點地理位置(傳播距離)有關的函數，而dξ是由于電離層等效高度隨機變化引起的隨機變量。

假定δh(d,t)在傳播路徑上各點都是呈正態分布，且其標準偏差相等，則它們的積分亦是呈正態分布，且其期望值應為

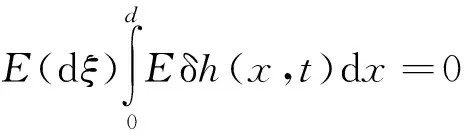
(18)

方差應為

(19)

式中：

(20)

是等效高度隨機起伏沿傳播路徑的歸一化自相關函數。

若認為等效高度隨機起伏的自相關函數能用指數函數描述，且相關距離為L，則

(21)

將式(21)代入式(19)可得

(22)

當d>>L，則

D(dξ)≈2LdD(δh)

(23)

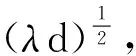
(24)

由式(16)和(8)可以看出，接收點場強幅度的相對變化為

(25)

式(25)中，僅有dξ是隨機變量，故接收點場強起伏標準偏差可估計為

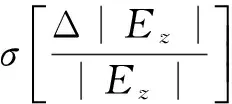
(26)

當接收點距離發射點相當遠時，高階模已衰減至不起作用，則有

M(d)≈|F1|

(27)

(28)

在此情況下，式(26)可以退化為

(29)

如果將場強起伏標準偏差以dB表示(d以千km為單位)，則應有

(30)

由文獻[3]可知

(31)

式中，系數K在白天取為1，夜晚取2.4.

故式(30)可進一步表示為

(32)

式中

(33)

圖2給出了白天大同到海口路徑上場強標準偏差隨距離的變化曲線。

圖2 白天大同-海口路徑上多模干涉區場強起伏標準偏差隨傳播距離地變化(頻率12.5 kHz)

從圖2可以明顯看出：由于存在多模干涉，在多模干涉區場強的穩定性比較差，尤其是在距發射臺600 km范圍內；在多模干涉區公式(29)不適用，但是在單模干涉區式(33)計算結果與式(29)結果能夠較好的吻合；我們提出的標準偏差估計公式的計算結果與文獻[8]實測數據的標準偏差一致且吻合良好。對比結果表明，我們提出的多模干涉區場強起伏標準偏差公式可以更準確地反映出整個傳播路徑上場強的起伏變化。

5. 結 論

目前，國內對多模區VLF場強起伏標準偏差的估計方法研究較少，沒有提出明確的場強起伏標準偏差的公式。國外也只是給出了單模干涉區場強起伏標準偏差估計的經驗公式。而我們給出的場強起伏標準偏差估計公式，可以較好的應用于多模干涉區、單模干涉區及場強極小點附近。通過與實測數據的對比，證明此場強起伏標準偏差估計公式能夠較準確地反映出電離層的隨機變化對傳播路徑上場強的穩定性的影響。此偏差估計公式對VLF通信可靠性的研究具有重要意義。

[1] WAIT J R and SPIES K P. Characteristics of the earth-ionosphere wavequide for VLF radio wave[M]. NBS Tech note, No.300, 1964.

[2] GALEJS J. Terrestrial propagation of long electromagnetic wave[M]. NewYork: Pergamon press, 1972.

[3] WATT A D. VLF radio engineering[M]. NewYork: Pergamon press, 1967.

[4] PAN Weiyan and TIAN Yushu. Multi mode interference and phase stability of VLF wave propagation[C]//International Symposium on Radio Propagation, 1988: 40-43.

[5] 潘威炎. 長波超長波極長波傳播[M]. 成都: 電子科技大學出版社, 2004.

[6] 潘威炎, 田育庶, 等. 甚低頻(VLF)無線電系統場強與相位計算方法[S]. 中華人民共和國國家軍用標準, 1994.

[7] CCIR report 717-1.World atlas of ground conductivities[R]. 1982.

[8] WEN F R and XIONG H. The multimode interference of vlf radiowave propagating in near-medium ranges[C]//International Symposium on Radio Propagation, 1988: 36-39.