基于旋轉(zhuǎn)不變子空間均勻圓陣互耦自校正算法

王 鼎 吳 瑛

(解放軍信息工程大學(xué)信息工程學(xué)院，河南 鄭州 450002)

1.引 言

在超分辨率譜估計技術(shù)中，以多重信號分類法(MUSIC)算法[1]為代表的特征空間類算法引起了眾多學(xué)者的廣泛關(guān)注。但在實際工程應(yīng)用中，由于各種陣列誤差(例如幅相誤差、陣元位置誤差、互耦效應(yīng)等)時常存在，這些陣列誤差使得實際陣列流型與理想陣列流型有所不同，從而可能導(dǎo)致高分辨率算法性能的急劇下降[2-3]，甚至失效。因此，陣列誤差校正是超分辨率算法能否投入實用的重要環(huán)節(jié)。

與其他陣列誤差相比，陣元間的互耦效應(yīng)與陣列的電磁特性密切相關(guān)，也較為復(fù)雜，所以陣列的互耦補償與校正是一項重要的研究課題。目前，減少互耦影響的方法可分為兩大類：一類是先對互耦進行電磁測量或通過矩量法對互耦進行電磁計算[4-5]，然后利用互耦的測量值或計算值對高分辨率算法進行修正，然而互耦的測量和計算精度有時難以滿足實際工程需要，并且陣列互耦還會隨著周圍環(huán)境和電磁參數(shù)的變化而改變。另一類是將互耦校正問題轉(zhuǎn)化為參數(shù)估計問題，例如，文獻[6]-[8]提出了互耦有源校正方法，但該類方法對校正源的方位精度有較高要求，并且由于系統(tǒng)參數(shù)、信源的時變性以及空間信源的多徑效應(yīng)，使得該類方法在實際應(yīng)用中也會出現(xiàn)一些問題。文獻[9]-[11]提出了幾種互耦自校正方法，它們將信源方位和互耦參數(shù)根據(jù)某種代價函數(shù)進行聯(lián)合優(yōu)化，可在估計信源方位的同時完成互耦校正，但其中聯(lián)合估計所對應(yīng)的高維、多模非線性優(yōu)化帶來了較大運算量和局部收斂等問題。針對該缺點，文獻[12]-[14]利用均勻線陣互耦矩陣的Toeplitz性，分別提出了幾種不同的互耦自校正方法，這些方法都無需求解高維非線性優(yōu)化問題，實現(xiàn)難度相對較小，但它們都只能應(yīng)用于均勻線陣。眾所周知，相比于均勻線陣，均勻圓陣存在很多自身的優(yōu)勢，文獻[15]-[16]針對均勻圓陣提出了互耦自校正方法，其中利用均勻圓陣互耦矩陣的循環(huán)Toeplitz性，同樣避免了高維、多模非線性優(yōu)化問題，但所涉及到的譜峰搜索仍然需要較大運算量，并且與多重信號分類(MUSIC)算法不同的是，在文獻[15]-[16]的方法中，對每個搜索方位都需要計算矩陣的特征值、行列式或者是逆矩陣，因此運算量遠大于MUSIC算法中計算陣列流型向量的二次型。

眾所周知，ESPRIT算法[17]可以避免高分辨率算法中的譜峰搜索，只是該算法對陣型具有一定要求。盡管均勻圓陣不具備ESPRIT算法的要求，但通過模式空間轉(zhuǎn)換技術(shù)[18]可將ESPRIT算法應(yīng)用其中。然而，當(dāng)考慮圓陣的互耦效應(yīng)時，直接利用上述算法必然會失效，對此該文提出了一種基于ESPRIT技術(shù)和模式空間轉(zhuǎn)換技術(shù)的均勻圓陣互耦自校正算法，該算法避免了譜峰搜索以及高維、多模非線性優(yōu)化，能夠直接給出信源方位和互耦向量的閉式解，針對模式空間轉(zhuǎn)換偏差對參數(shù)估計的消極影響，文中基于文獻[19]中的思想，給出了一種能夠在互耦影響下模抵消式空間轉(zhuǎn)換偏差的方法。

2.互耦影響下的陣列信號模型

假設(shè)一個M元均勻圓陣，現(xiàn)有D個不相關(guān)信源到達該陣列，復(fù)包絡(luò)分別為s1(t)，s2(t)，…，sD(t)，相應(yīng)的方位分別為θ1，θ2，…，θD，則在考慮互耦的影響下，陣列的輸出響應(yīng)為

=CAs(t)+n(t)

(1)

a(θ)=[ejξcos(θ-φ0)ejξcos(θ-φ1)…ejξcos(θ-φM-1)]T

(2)

式中:φm=2πm/M和ξ=2πr/λ，其中r為圓周半徑，λ為信源波長，而r/λ為半徑波長比。式(1)中的C表示互耦矩陣，對于均勻圓陣，它可由復(fù)對稱循環(huán)Toeplitz矩陣進行建模[9]。例如，對于5元均勻圓陣，若僅考慮最近鄰的2個和3個陣元之間的互耦效應(yīng)，其互耦矩陣分別具有如下結(jié)構(gòu)

(3)

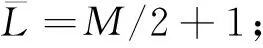
根據(jù)式(1)可得陣列輸出的協(xié)方差矩陣為

Rx=E[x(t)xH(t)]=CARsAHCH+σ2IM

(4)

式中： σ2為噪聲功率；Rs=E[s(t)sH(t)]為信源協(xié)方差矩陣。下文將考慮如何在已知Rx的基礎(chǔ)上利用ESPRIT技術(shù)估計信源方位和互耦因子。

3.互耦影響下均勻圓陣的模式空間轉(zhuǎn)換

3.1 理想條件下均勻圓陣的模式空間轉(zhuǎn)換

若在均勻圓陣中利用ESPRIT算法，模式空間轉(zhuǎn)換是一項重要環(huán)節(jié)，下面不妨直接將其引出，具體細節(jié)可見文獻[18]。實際中的均勻圓陣可看作是連續(xù)圓陣的離散采樣，其第k個模式的激勵向量為

(5)

而第k個相位模式的方向圖為

=jkJk(ξ)ejkθ+εk(θ) (-K≤k≤K)

(6)

式中：g=Mq-k和h=Mq+k；K表示最大模式數(shù)，其取值為[18]K≈?2πr/λ]。式(6)中右邊等式第一項jkJk(ξ)ejkθ稱為主項，它等于連續(xù)圓陣的遠場方向圖，第二項εk(θ)稱為殘余項，它是對連續(xù)圓陣進行離散采樣所引起。為了使主項在數(shù)值上占主導(dǎo)地位，需要滿足條件[18]M>2K，而模式空間轉(zhuǎn)換矩陣為

FH=ΣVH

(7)

式中

(8)

根據(jù)式(6)，在忽略殘余項的基礎(chǔ)上可近似得

(9)

式中

(10)

不難看出，式(9)中的Jξ是常量矩陣，而a0(θ)具有Vandermode結(jié)構(gòu)，它能為ESPRIT技術(shù)的應(yīng)用提供必要的理論基礎(chǔ)。

3.2 互耦影響下均勻圓陣的模式空間轉(zhuǎn)換

為了分析互耦影響下均勻圓陣的模式空間轉(zhuǎn)換，這里首先定義3個M階置換矩陣

(11)

則不難證明如下等式

(12)

式中c(i)表示向量c中的第i個元素。于是可得

(13)

進一步可得

=Γa0(θ)

(14)

式中

(15)

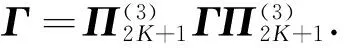
(16)

根據(jù)式(10)，式(15)和式(16)可知τk的表達式為

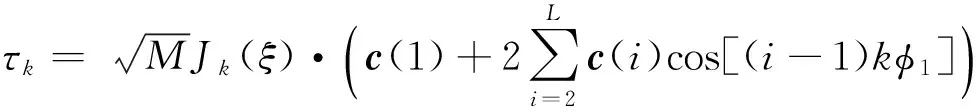
(k=0，1，…，K)

(17)

根據(jù)式(14)可知，模式空間轉(zhuǎn)換可將互耦影響下的均勻圓陣流型向量近似等效為存在幅相誤差的虛擬均勻線陣流型向量，并且該幅相誤差矩陣還滿足中心對稱性。

4.基于ESPRIT技術(shù)的均勻圓陣互耦自校正算法

4.1 算法的基本原理

4.1.1 估計信源方位

令R1=Rx-σ2IM=FHCARsAHCHF，則根據(jù)式(14)，對R1進行模式空間轉(zhuǎn)換可得

(18)

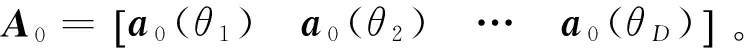
(19)

Γ12US2=US1Ψ

(20)

(21)

(22)

進一步可得

Γ12WS2=WS1Ψ-1

(23)

類似于文獻[20]中的分析方法，根據(jù)式(20)可得求解τ的優(yōu)化問題如下

(24)

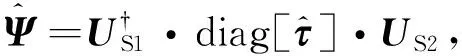
(25)

(26)

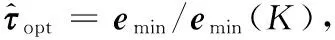
(27)

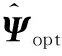
(28)

式中angle(·)表示復(fù)數(shù)相位。

4.1.2 估計互耦因子

(k=2，3，…，K)

(29)

根據(jù)式(29)可得關(guān)于互耦向量c的線性方程組如下

(Λ1G1-Λ2G2)c=Gc=0

(30)

式中G=Λ1G1-Λ2G2，其中

(31)

(32)

(33)

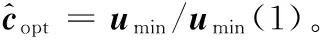
至此文中已經(jīng)給出了基于ESPRIT技術(shù)的均勻圓陣互耦自校正算法的關(guān)鍵環(huán)節(jié)，下小節(jié)將針對上述算法進行進一步討論和改進。

4.2 算法的進一步討論和改進

4.2.1 方位估計的“π-模糊”問題

(34)

4.2.2 模式空間轉(zhuǎn)換偏差的消除

盡管式(6)中的殘余項εk(θ)可以通過設(shè)置陣列參數(shù)將其影響減弱，但它畢竟還會對后續(xù)算法產(chǎn)生影響。文獻[19]對模式空間轉(zhuǎn)換矩陣F進行了修正，用以消除殘余項對后續(xù)算法的影響，這里將基于該方法，針對互耦存在的條件下對F進行修正。

若考慮殘余項，則可將式(14)改寫為

(35)

式中：ε(θ)=[ε-K(θ) …ε-1(θ)ε0(θ)ε1(θ) …εK(θ)]T。根據(jù)文獻[19]中的討論可知，在數(shù)值上，εk(θ)幾乎全部由累加號中的“q=1”項所決定，于是不妨將式(35)進一步簡化為

(36)

式中

(37)

(38)

(39)

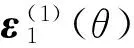
(40)

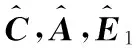
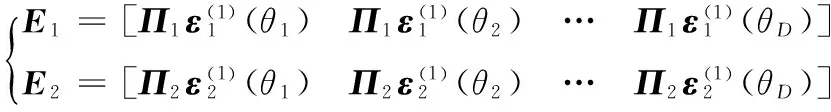
(41)

(42)

于是可得修正后的模式空間轉(zhuǎn)換矩陣為

(43)

實際計算中，為了取得更高的參數(shù)估計精度，可利用式(43)進行多次抵消，并在每次抵消后再更新信源方位和互耦向量的估計值。

4.2.3 算法的計算步驟

下面給出文中提出的基于ESPRIT技術(shù)的均勻圓陣互耦自校正算法的全部計算步驟。

步驟1：利用式(7)和式(8)計算模式空間轉(zhuǎn)換矩陣FH；

步驟2：對R1進行模式空間轉(zhuǎn)換得到R2，并對R2進行特征分解，從而得到信號子空間US；

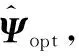
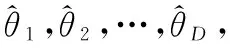
由于上述算法利用了ESPRIT技術(shù)，從而避免了很多互耦自校正算法中所需要的譜峰搜索以及多模非線性優(yōu)化問題，下節(jié)將通過仿真實驗驗證上述算法的有效性。

5.仿真實驗

5.1 驗證算法有效性的仿真實驗

仿真條件：假設(shè)陣列流型為9元均勻圓陣，半徑波長比為0.7，并且僅考慮相鄰3個陣元之間的互耦效應(yīng)，其互耦因子分別為1，0.12-0.18j和-0.05+0.06j，現(xiàn)有2個等功率高斯信源到達該陣列，方位分別為42°和80°，信噪比均為10 dB，算法中模式空間轉(zhuǎn)換的最大模式數(shù)為4，采樣點數(shù)為500.

仿真結(jié)論：圖1和圖2分別給出了在200次獨立實驗中，文中算法所估計出的信源方位和互耦因子的數(shù)值，圖中分別給出了“抵消模式空間轉(zhuǎn)換偏差(這里抵消3次)”和“不抵消模式空間轉(zhuǎn)換偏差”兩種情況下的數(shù)值結(jié)果。從圖1和圖2中可以看出文中算法的有效性，并且如果不抵消模式空間轉(zhuǎn)換偏差，則無論是對于信源方位估計還是互耦因子估計都存在一個確定固有偏置，而通過抵消模式空間轉(zhuǎn)換偏差可以很好的消除這種偏置。圖3和圖4分別給出了在200次獨立實驗中，2個信源的方位估計真實值和虛假值所對應(yīng)的f(θ)的數(shù)值。從圖3和圖4中不難看出，方位估計真實值對應(yīng)的f(θ)總是遠小于虛假值對應(yīng)的f(θ)，從而驗證了文中第4.2.1小節(jié)中給出的去“π-模糊”方法的有效性。

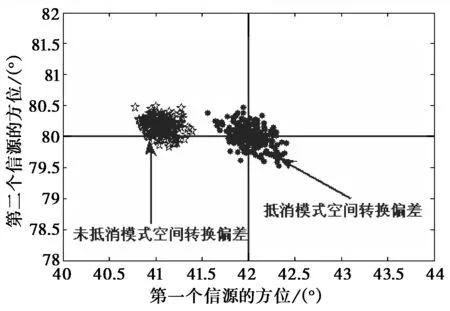
圖1 文中算法所給出的信源方位估計值

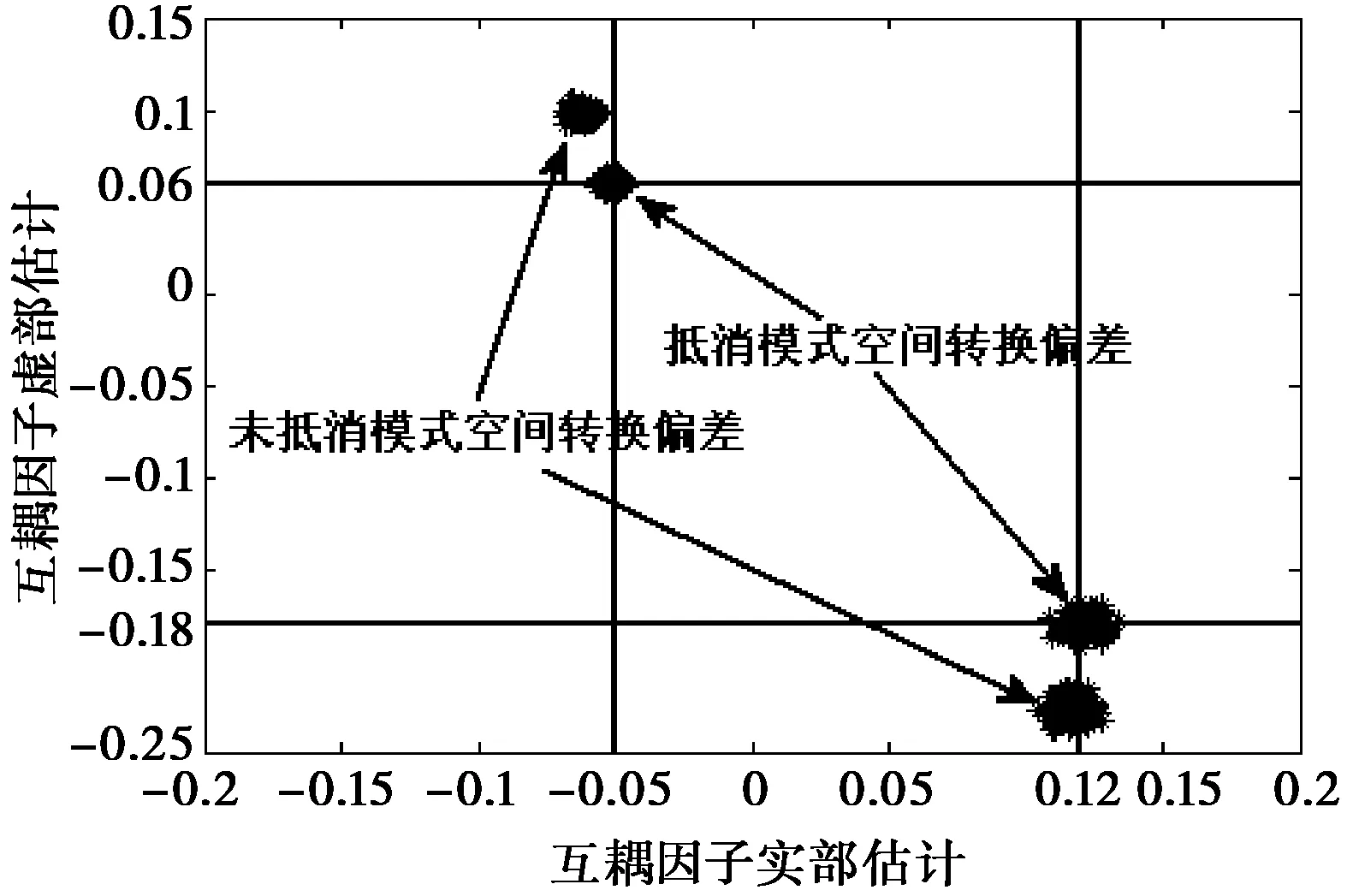
圖2 文中算法所給出的互耦因子估計值

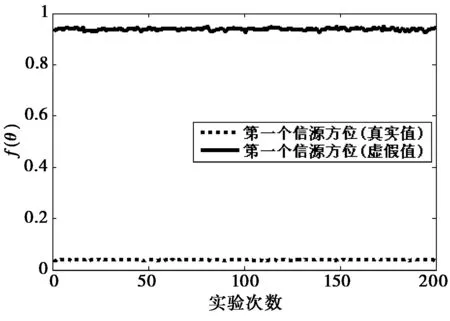
圖3 第一個信源方位估計的真實值和虛假值對應(yīng)的f(θ)

圖4 第二個信源方位估計的真實值和虛假值對應(yīng)的f(θ)

5.2 驗證算法估計性能的仿真實驗

仿真說明：為了驗證文中算法通過考慮互耦校正能夠為信源方位估計帶來好處，這里不妨與不考慮互耦影響的均勻圓陣ESPRIT算法進行比較，這里的均勻圓陣ESPRIT算法是指先對圓陣進行模式空間轉(zhuǎn)換，然后直接利用ESPRIT算法進行方位估計，但不考慮互耦效應(yīng)，而且這里的均勻圓陣ESPRIT算法也抵消模式空間轉(zhuǎn)換偏差，并且抵消次數(shù)與文中算法相同，下面要做的比較是將文中的算法分別與上述均勻圓陣ESPRIT算法在“存在互耦”和“沒有互耦”這兩種情況進行比較。仿真條件同第5.1小節(jié)，只是改變信源信噪比和采樣點數(shù)。

仿真結(jié)論：圖5和圖6分別給出了信源方位估計均方根誤差和測向成功概率隨著信噪比的變化曲線，圖7給出了文中算法的互耦因子估計均方根誤差隨著信噪比的變化曲線。需要指出的是，圖中的符號“o”和“▽”標(biāo)注的曲線分別是在采樣點數(shù)為400和800條件下所做的實驗，并且算法中抵消模式空間轉(zhuǎn)換偏差的次數(shù)為3次。從圖5和圖6中不難看出，文中算法的性能明顯高于“存在互耦”情況下的均勻圓陣ESPRIT算法，并與“沒有互耦”情況下的均勻圓陣ESPRIT算法性能較為接近，只是在信噪比較低時，文中算法的性能略差，但隨著信噪比的增加，兩者的性能趨于一致。最后，這里還通過一個仿真實驗驗證抵消模式空間轉(zhuǎn)換偏差所帶來的好處。仿真條件不變，圖8給出了文中的算法在“抵消模式空間轉(zhuǎn)換偏差(抵消次數(shù)為3次和4次)”和“不抵消模式空間轉(zhuǎn)換偏差”時的信源方位估計均方根誤差曲線，從圖8可以明顯地看出抵消模式空間轉(zhuǎn)換偏差所帶來的好處，而且隨著信噪比的增大而更加明顯，這是因為模式空間轉(zhuǎn)換偏差是一種確定性誤差，它不會隨著信噪比的增大而減少。此外，從圖8還可以看出抵消3次和4次的性能已經(jīng)非常接近了，這就意味著算法所需要的抵消次數(shù)不會很多。

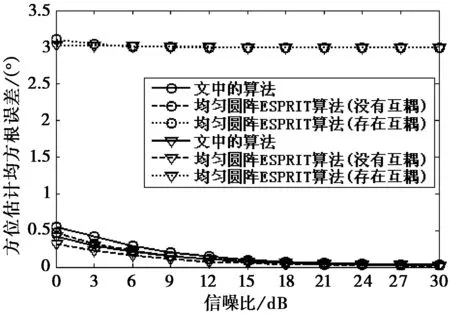
圖5 信源方位估計均方根誤差曲線

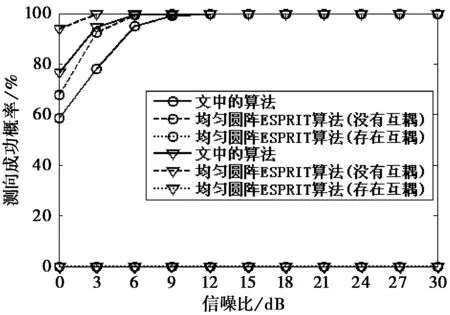
圖6 測向成功概率曲線

圖7 互耦因子估計均方根誤差曲線

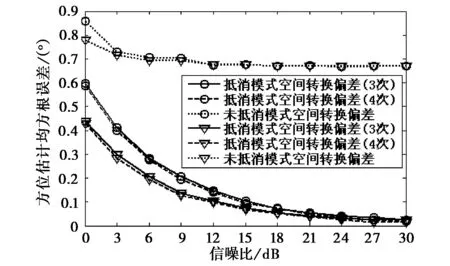
圖8 抵消模式空間轉(zhuǎn)換偏差和不抵消時的性能比較

6.結(jié) 論

針對均勻圓陣互耦自校正問題，該文提出了一種基于ESPRIT技術(shù)和模式空間轉(zhuǎn)換技術(shù)的互耦自校正算法，該算法避免了很多互耦自校正算法中的譜峰搜索以及高維、多模非線性優(yōu)化問題，能夠直接得到信源方位和互耦向量的閉式解。仿真實驗驗證了文中算法的有效性，并且其性能明顯高于“存在互耦”情況下的均勻圓陣ESPRIT算法，而與“沒有互耦”情況下的均勻圓陣ESPRIT算法性能較為接近，只是在信噪比較低時，文中算法的性能略差，但隨著信噪比的增加，兩者的性能趨于一致。

[1] SCHMIDT R O.Multiple emitter location and signal parameter estimation[J].IEEE Transactions on Antennas and Propagation，1986，34(3)：267-280．

[2] FERRéOL A，LARZABAL P，VIBERG M.On the asymptotic performance analysis of subspace DOA estimation in the presence of modeling errors：case of MUSIC[J].IEEE Transactions on Signal Processing，2006，54(3)：907-920．

[3] 王 鼎，吳 瑛.小幅相誤差下MUSIC的測向成功概率和分辨概率[J].電波科學(xué)學(xué)報，2010，25(4)：749-756．

WANG Ding，WU Ying.Direction-finding success probability and resolution probability of MUSIC algorithm in the presence of small gain-phase errors[J].Journal of Radio Science，2010，25(4)：749-756.(in Chinese)

[4] ADVE R S，SARKAR T K.Compensation for the effects of mutual coupling on direct data domain adaptive algorithms[J].IEEE Transactions on Antennas and Propagation，2000，48(1)：86-94．

[5] 伍裕江，聶在平.一種新的互耦補償方法及其在DOA估計中的應(yīng)用[J].電波科學(xué)學(xué)報，2007，22(4)：541-545．

WU Yujiang，NIE Zaiping.A new mutual coupling compensation method and its application to DOA estimation[J].Journal of Radio Science，2007，22(4)：541-545.(in Chinese)

[6] SEE C M S.Sensor array calibration in the presence of mutual coupling and unknown sensor gains and phases[J].Electronics Letters，1994，30(5)：373-374．

[7] JAFFER A G.Constrained mutual coupling estimation for array calibration[C]∥Proceeding of the 35th Asilomar Conference on Signal，Systems and Computers，2001：1273-1277．

[8] 王 鼎，吳 瑛.一種利用互耦矩陣稀疏性的陣列誤差有源校正改進算法[J].信號處理，2009，25(9)：1414-1420．

WANG Ding，WU Ying.An improved active array errors calibration algorithm using the sparseness of mutual coupling matrix[J].Signal Processing，2009，25(9)：1414-1420.(in Chinese)

[9] FRIEDLANDER B，WEISS A J.Direction finding in the presence of mutual coupling[J].IEEE Transactions on Antennas and Propagation，1991，39(3)：273-284．

[10] SVANTESSON T.Mutual coupling compensation using subspace fitting[C]∥ Proceedings of the 2000 IEEE Sensor Array and Multichannel Signal Processing Workshop，Mar，2000：494-498．

[11] SELLONE F，SERRA A.A novel mutual coupling compensation algorithm for uniform and linear arrays[J].IEEE Transactions on Signal Processing，2007，55(2)：560-573．

[12] 王布宏，王永良，陳 輝.均勻線陣互耦條件下的魯棒DOA估計及互耦自校正[J].中國科學(xué)E輯：信息科學(xué)，2004，34(2)：229-235．

WANG Buhong，WANG Yongliang，CHEN Hui.Robust DOA estimation and mutual coupling self-calibration algorithm for uniform linear array[J].Science in China Series E：Technological Sciences，2004，34(2)：229-235.(in Chinese)

[13] YE Z F，DAI J S，XU X，et al.DOA estimation for uniform linear array with mutual coupling[J].IEEE Transactions on Aerospace and Electronic Systems，2009，45(1)：280-288．

[14] XU X，YE Z F，ZHANG Y F.DOA estimation for mixed signals in the presence of mutual coupling[J].IEEE Transactions on Signal Processing，2009，57(9)：3523-3532．

[15] QI C，WANG Y，ZHANG Y，et al.DOA estimation and self-calibration algorithm for uniform circular array[J].Electronics Letters，2005，41(20)：1092-1094．

[16] LIN M，YANG L.Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling[J].IEEE Antennas Wireless Propagation Letters，2006，5，315-318．

[17] ROY R，KAILATH T.ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Transactions on Acoustics，Speech and Signal Processing，1989，37(7)：984-995．

[18] MATHEWS C P，ZOLTOWSKI M D.Eigenstructure techniques for 2D angle estimation with uniform circular arrays[J].IEEE Transactions on Signal Processing，1994，42(9)：2395-2407．

[19] BELLONI F，KOIVUNEN V.Beamspace transform for UCA：error analysis and bias reduction[J].IEEE Transactions on Signal Processing，2006，54(8)：3078-3089．

[20] LIAO Bin，LIAO Guisheng.A method for array gain and phase uncertainties calibration based on ISM and ESPRIT[J].Journal of Systems Engineering and Electronics，2009，20(2)：223-228．