我國鐵路運輸與第二產業發展的動態關系研究

張凌潔，馬立平

（首都經濟貿易大學 統計學院，北京 100026）

目前，我國處于工業化加速發展時期，第二產業比重穩步上升并居國民經濟的主體地位。作為現代經濟運行重要組成部分的鐵路運輸，密切影響著第二產業的發展。從經濟規模上，第二產業的生產規模代表區域內部的貨物生產規模，而貨物生產規模與貨物周轉量有直接關系。無論這些貨物是作為居民最終消費使用，還是作為其他產業的中間產品投人使用，均會帶來區域的貨物運輸需求。第二產業的行業集中度與貨物周轉量有密切的關系。目前，國內相關研究大多是定性地分析鐵路運輸業在國民經濟中的重要地位，定量研究尤其是動態研究較少。因此，結合我國1978—2008 年鐵路運輸指標數據和第二產業增加值年度數據，基于 VAR 模型，運用協整理論、脈沖響應函數來研究其動態影響關系。

1 模型研究及應用

采用向量自回歸模型 (Vector Auto-regression，VAR)，選用貨運量和貨物周轉量x2作為研究鐵路運輸業的指標，全國第二產業增加值y作為第二產業經濟發展的指標。將第二產業增加值、貨運量、貨物周轉量這3個變量通過 VAR 模型的脈沖響應函數和方差分解技術，研究第二產業與鐵路運輸的相互響應關系及程度。為保證數據的可比性，以 1978 年為基期，計算得到各年實際增加值，再進行對數變換，然后分別把lny、lnx1和 lnx2的一階差分記為Δlny、Δlnx1和Δlnx2。

1.1 時間序列平穩性及其檢驗

時間序列的平穩性是指時間序列的統計特性不隨時間推移而發生變化的特性。采用增廣迪基-福勒檢驗 (Augmented Dickey-Fuller test，ADF檢驗)來判斷時間序列的平穩性，ADF檢驗用于檢驗序列是否服從有單位根的自回歸過程。下面分別對序列lny、lnx

1、lnx2進行檢驗，結果表明三者均不是平穩序列；再分別對序列Δlny、Δlnx1和Δlnx2進 行

ADF 檢驗，說明三者均為一階單整序列，檢驗結果如表1所示。

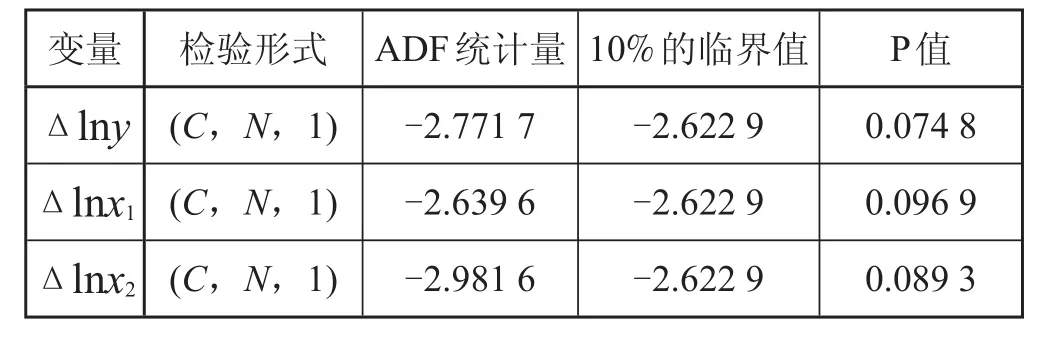
表 1 ADF 檢驗結果

注：檢驗形式 (C，N，1) 中的C、N和1分別表示單位根檢驗方程，包括常數項，不包括時間趨勢，滯后階數為 1。

1.2 確定向量自回歸模型階數

VAR 模型采用多方程聯立的形式，在每個方程中將每個內生變量對模型的全部內生變量的滯后值進行回歸，從而估計全部內生變量間的動態關系。VAR 模型除需要滿足平穩性條件外，還應確定滯后期k。如果滯后期太少，誤差項的自相關會很嚴重，并導致參數的非一致性估計。本研究對最優滯后期的選擇根據赤池消息準則 (AIC) 和施瓦茨準則 (SC) 來確定，當兩者達到最小時的階數為最優階數。通過檢驗可以看出，最優階數為3。

1.3 協整檢驗

在模型中3個變量同階單整，滿足協整檢驗的前提條件，為了探索變量之間是否具有長期的穩定關系，需要進行協整檢驗。本研究采用基于 VAR模型的 Johansen 協整檢驗。協整檢驗模型實際上是對無約束 VAR 模型進行協整約束后得到的 VAR 模型，該模型的滯后期是無約束 VAR 模型一階差分變量的滯后期。由于無約束 VAR 模型的最優滯后期為k，所以將協整檢驗的 VAR 模型滯后期確定為k-1。本研究確定模型滯后期為 2，采用無截距和趨勢項的檢驗方式。從表2中可以看出，在 5% 的顯著性水平下，跡檢驗和最大特征根檢驗都認為變量之間不存在協整關系，這說明第二產業的發展與貨運量和貨物周轉量的發展之間不存在長期的均衡關系。

1.4 建立向量自回歸模型 (VAR)

由于Δlny、Δlnx1和Δlnx

2均可看作內生變量，因此可以建立二階的無約束 VAR 模型。經過檢驗，模型是顯著的，說明該 VAR 模型的結構是穩定的。通過基于 VAR 模型的脈沖響應函數和方差分解，可以測算Δlny對Δlnx1和Δlnx

2沖擊的響應。觀察特征根的分布，模型特征根均小于 1，說明模型的結構是穩定的，可以進行脈沖響應分析與方差分解分析。

1.5 脈沖響應函數

表 2 Johansen 協整檢驗

脈沖響應函數是用于衡量隨機擾動項的一個標準差沖擊對其他變量當前和未來取值的影響軌跡，能夠比較直觀地刻畫出變量之間的動態交互作用及效應。

基于 VAR (3) 模型運用模擬沖擊法，對系統施加外部沖擊，計算各變量對沖擊的反應，并將各變量的瞬時反應加總，考察其對外部沖擊的長期總反應。圖1—圖5分別表示Δlny對Δlnx1、Δlnx2對一個標準差隨機擾動項的累積脈沖響應，即分別顯示了其對自身和其他變量的標準差沖擊的長期總反應。在圖 1—圖5中，上下兩條虛線分別代表正負 2倍標準差偏離帶，中間實踐代表脈沖相應函數，在模型中將響應的時間長度設定為 15 年。模型通過顯著性檢驗且調整的可決系數均大于 0.95。

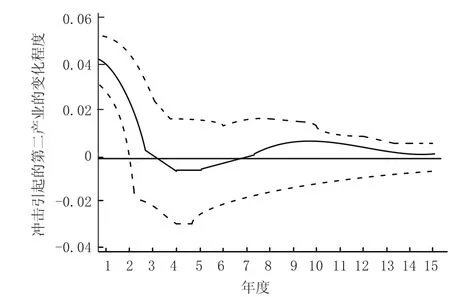
圖 1 第二產業對其自身一個標準差的脈沖相應圖

圖 2 貨物周轉量對第二產業的脈沖相應圖

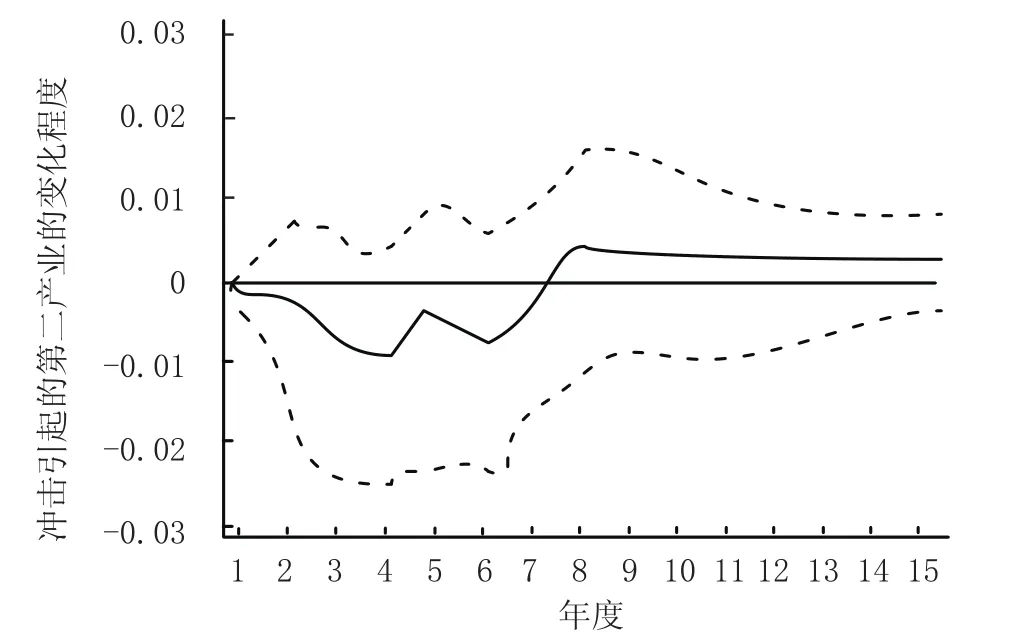
圖 3 貨運量對第二產業的脈沖相應圖

圖 4 第二產業對貨物周轉量的脈沖相應圖

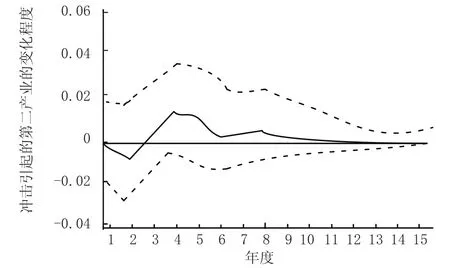
圖 5 第二產業對貨運量的脈沖相應圖

從圖1可以看出，第二產業增加值對其自身一個標準差的沖擊響應開始是正的響應，到第三期由一個小小的波動變為負相應，第七期轉為正向，慢慢收斂。從圖2可以看出，貨物周轉量的沖擊引起經濟增長變化的脈沖響應過程是當在第一期給貨物周轉量一個標準差的沖擊后 (即貨物周轉量增加)，對經濟增加值是一個負響應，在第四期到達頂點后逐漸收斂并轉為正向收斂。從圖3可以看出， 貨運量的沖擊引起經濟增加值的變化的脈沖響應過程是當在第一期給出一個標準差的沖擊，對經濟增加值是一個負響應，在第四期到達頂點后逐漸收斂，到第七期出現正響應并趨于平穩。圖4、圖5是第二產業增加值對貨運量、貨物周轉量的脈沖響應圖，在第一期給出經濟一個標準差的沖擊后，從第二期開始對貨運量一直呈現正向效應，并且快速收斂，達到穩定狀態；第二產業增加值對貨物周轉量有短期的負向效應，第三期即為正向效應并快速收斂達到穩定狀態。

1.6 方差分解

方差分解表示當系統的某個變量受到一個單位的沖擊以后，以變量的預測誤差方差百分比的形式反映向量之間的交互作用程度，其基本思想是把系統中每個內生變量的變動按其成因分解為與各方程隨機擾動項相關聯的各組成部分，以了解各隨機擾動項對模型內生變量的相對重要性。利用方差分解技術分析鐵路運輸對第二產業增加值的貢獻率 (見表3)。

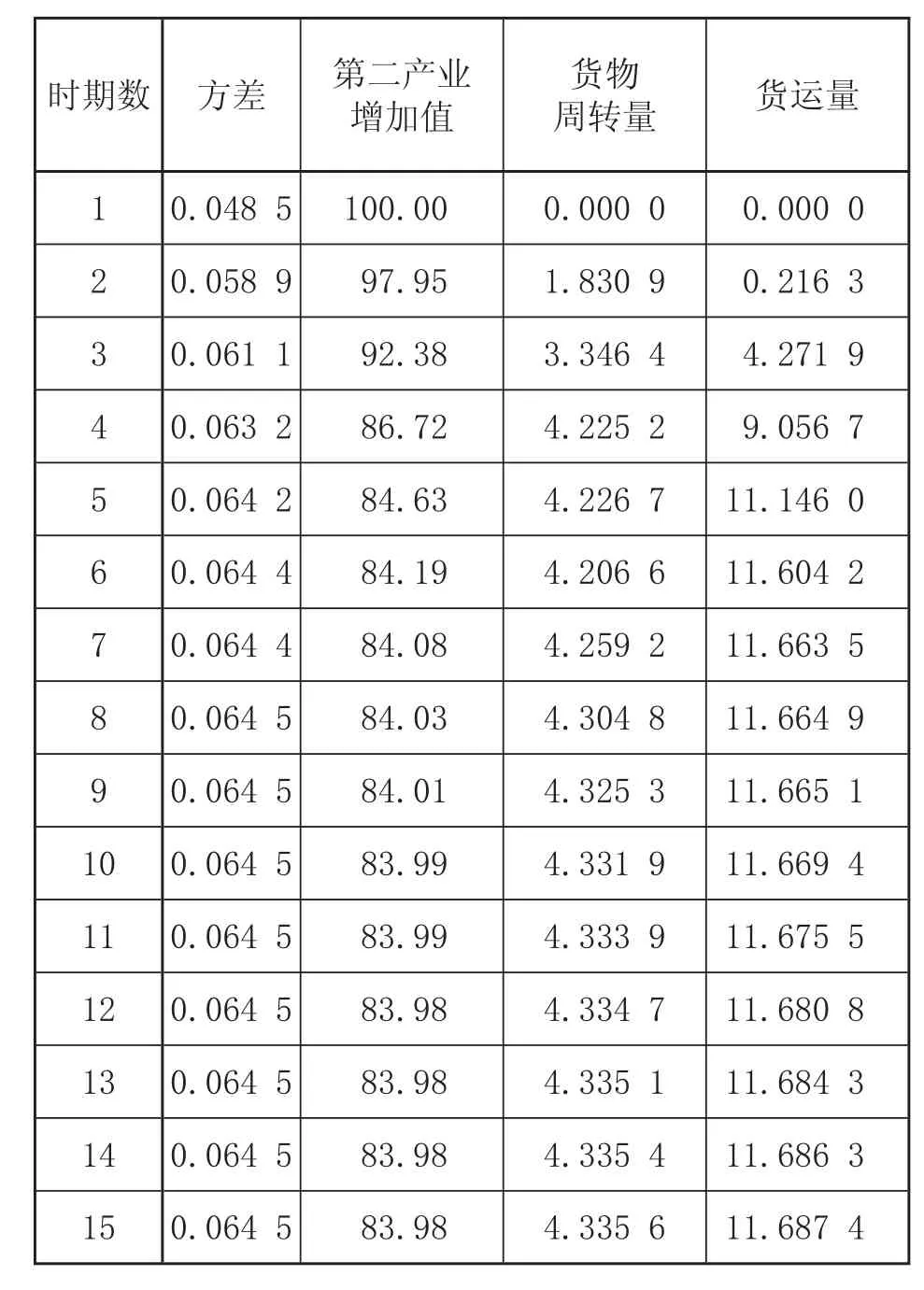
表 3 第二產業增加值的方差分解表

從表3中可以看出，第二產業增加值的波動在第一期只受自身波動沖擊的影響，這是由于在建立VAR 模型時，把Δlny作為第一個因變量，從第二期開始來自第二產業增加值自身的擾動逐漸下降，在第四期受自身影響顯著下降，在第十期后基本穩定在 83% 左右，但仍起主要作用，這與脈沖響應的結論相一致。貨運量變化從長期來看，能夠影響第二產業增加值變化的 11.69% 左右；而貨物周轉量對第二產業增加值變化的影響程度能力較小，僅為4.34% 左右。

2 基本結論

基于 1978—2008 年的第二產業增加值和貨運量與貨物周轉量數據，對以上變量采用時間序列的平穩性檢驗、協整檢驗的實證分析表明，第二產業增加值和貨運量與貨物周轉量三者之間并不存在協整關系。同時，構建了第二產業和交通運輸的VAR(3) 模型，并在此基礎上利用脈沖響應函數分析了3個變量之間的關系，對因變量預測誤差進行分解得出以下結論。

（1）在 5% 顯著水平上，第二產業增加值和貨運量與貨物周轉量并不存在長期穩定的均衡關系；從長期來看，第二產業增加值不僅能自我促進，而且對貨運量與貨物周轉量發展有顯著正效應，這不僅說明我國的經濟增長具有一定的慣性，而且反映出經濟增長的預期水平對鐵路運輸部門經濟實際運行態勢具有顯著影響。

（2）貨運量和貨物周轉量對第二產業增加值的初期呈現負效應，到達第七期時才轉向正向效應，但效果并不顯著，說明鐵路運輸業對第二產業增長的促進效應仍未激活。通過對第二產業增加值的方差分解，引起其發生變化的主要原因是自身的隨機擾動項沖擊和貨運量沖擊，貨物周轉量的貢獻率非常小。

3 結束語

通過分析，貨運量和貨物周轉量對第二產業增加值的促進效應并不十分顯著，第二產業主要是靠自身的內生增長。因此，從長期來看，鐵路建設應著力外延擴張，結合區域產業結構調整，優化運輸資源配置，這將促使鐵路運輸業與第二產業之間的關聯度更加緊密，起到相互帶動的長期作用。