大視場數字式太陽敏感器設計*

屠斌杰，韓 柯，王 昊，白 劍，金仲和

(浙江大學信息與電子工程學系，杭州310027)

太陽敏感器是衛星姿態確定系統中十分重要的測量器件。太陽敏感器通過測量太陽光線與衛星某一體坐標之間的夾角，從而確定太陽在敏感器本體坐標系中的位置，然后通過坐標矩陣變換得到太陽在衛星本體坐標系中的位置，最終在衛星的姿態系統中求得衛星的姿態，即衛星在空間的方位[1]。

隨著衛星對姿態控制精度要求的日益提高以及小衛星、皮衛星等微小衛星的發展，太陽敏感器逐漸向著小型化、模塊化、長壽命的方向發展[2]。目前，很多的太陽敏感器采用了APS面陣來代替CCD作為圖像傳感器，由于APS面陣在體積、功耗上的優勢，使得太陽敏感器能有效地朝著上述方向發展。

由于受圖像傳感器像平面尺寸及掩膜安裝位置限制，普通數字式太陽敏感器的視場范圍一般在±60°左右，當初始姿態角度不在視場范圍內時，此類太陽敏感器就無法正常工作。為了解決這一問題，國內外研究者提出了一些增大數字式太陽敏感器的方案。如將多個太陽敏感器組合成一個太陽敏感器，或者設計特殊的球狀掩膜結構[3]，這些設計上的改變雖然增大了敏感器的視場，卻也同時帶來一些問題，如系統體積、質量及功耗的增加，或者以犧牲敏感器的測量精度為代價。

針對這些不足，本文提出了一種基于全景環形光學鏡頭的大視場數字式太陽敏感器設計方法，其視場大小為120°×180°，與±60°的視場大小相比具有很大優勢。同時該敏感器的質量、體積和功耗非常適合微小衛星發展要求，分別為250 g、55 mm×55 mm×50 mm和300 mW。敏感器的測量精度為0．02°，能滿足普通定姿系統的精度要求。

1 系統設計

1．1 傳統數字式太陽敏感器設計

目前常見的數字太陽敏感器工作原理如圖1所示，主要是運用小孔成像原理對太陽進行成像，使其光斑投射在圖像傳感器上，然后信息處理電路用某種算法提取像光斑中心位置，并測算出太陽入射角[4]。由圖1的幾何關系，我們可以得出太陽光線和已知坐標軸之間的角度關系[5]:

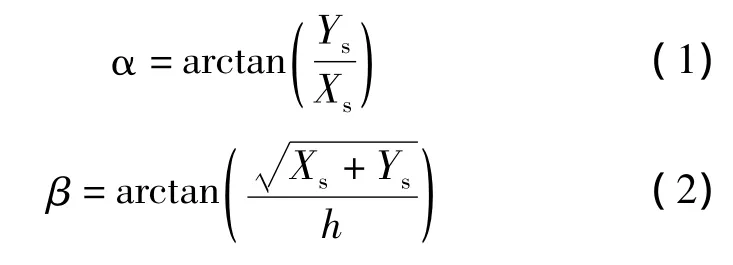
其中α、β分別為太陽光線在坐標軸X、Z上的角度，Xs、Ys為太陽光線經小孔后在像平面上所成像的坐標值，h為掩膜與像平面之間的距離。

根據圖1分析可知，要想增加角度測量范圍，則必須增大圖像傳感器像平面的大小或減小h的值，前者不滿足小型化要求，后者會降低測量精度。

在實際應用中，設計者會根據具體要求將掩膜上小孔個數和排列方式進行適當修改，此類修改能提高太陽敏感器的精度，但對增大其視場是沒有幫助的。

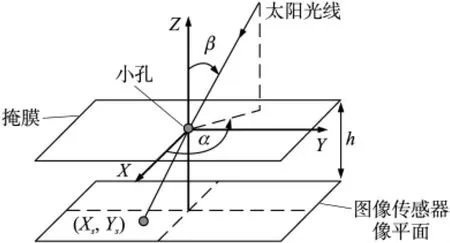
圖1 常見數字太陽敏感器工作原理圖

1．2 全景環形光學鏡頭介紹

為了克服傳統太陽敏感器視場小的缺點，本文設計了一種新型大視場太陽敏感器，光學系統由全景環形光學鏡頭和濾光膜組成。

全景環形光學鏡頭的工作原理如圖2所示，為獲得360°全景像，人們基于延展法的思想提出了平面圓柱透視法(Flat Cylinder Perspective:FCP)，這種透視法將一個柱面視場投影到二維像平面[6]。在FCP映射中，所有的平行線匯聚到一點，能夠成像部分是θ角的兩條邊繞軸旋轉360°后得到的三維立體區域，這一區域被投影到二維像面上的圓環內，像面上每一個同心圓是與軸成同一角度的點的軌跡。環形透鏡產生的環形像的高度對應與側向視場的范圍。2ψ角所代表的區域為盲區[7]。全景環形透鏡(Panoramic Annular Lens:PAL)是基于FCP透視法的一種光學鏡頭，在天文觀測、醫用內窺檢查等領域有著潛在的應用前景。

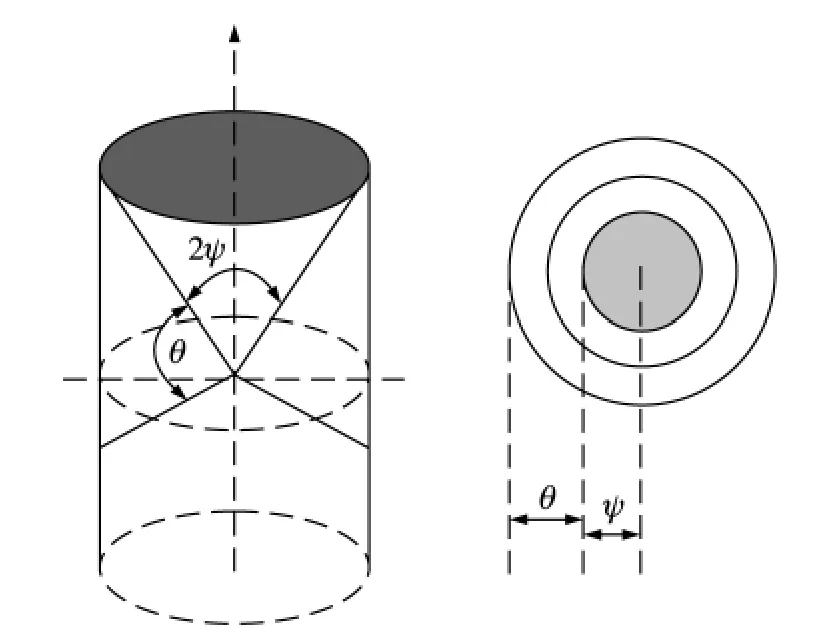
圖2 FCP工作原理示意圖

1．3 大視場數字式太陽敏感器設計

基于全景光學鏡頭，本文提出的大視場太陽敏感器如圖3所示。由圖1和圖3比較可知:傳統數字太陽敏感器成像對象是太陽光線經小孔后投射在像平面上的光斑，光斑的形狀和大小與太陽無關，只取決于小孔形狀及掩膜到像平面之間的距離。而本文研究的太陽敏感器成像對象則是太陽經PAL在像平面上的光斑，所以其大小和形狀由太陽和PAL決定。

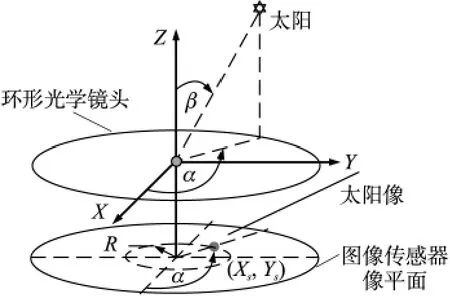
圖3 本文研究的太陽敏感器工作原理圖

此外，與常規光學系統相比，PAL所成的像，其像高滿足f－β的關系，即:

其中H為像高，f為PAL焦距，β為太陽光線與PAL光軸的夾角。

像高H可以通過計算光斑中心坐標到像平面中心的距離來獲取，而焦距f則由PAL設計時給出，那么要獲得角度β，只要計算出光斑的中心坐標即可。另一角度α的計算方法與傳統太陽敏感器一致。

根據前面的分析及圖3的幾何關系，我們可以得到本文提出的太陽敏感器角度測量方法，如式(4)、式(5):

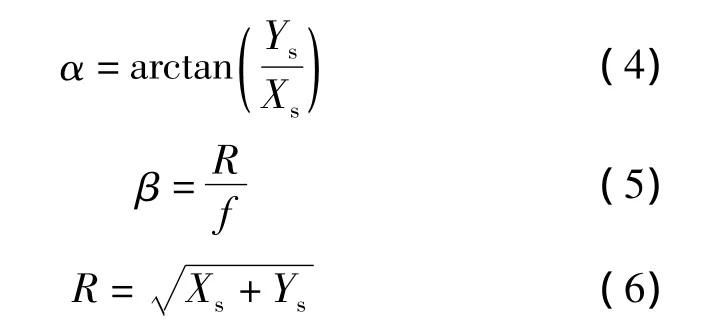
其中α、β分別為太陽光線在坐標軸X、Z上的角度，Xs、Ys為太陽光線經小孔成像后在像平面上所成像的坐標值，f為鏡頭焦距。

與傳統數字式太陽敏感器相比，本文的設計具有如下優點:

1．視場范圍大;

2．系統結構簡單;

3．更新率高。

2 系統實現

本文研究的數字式太陽敏感器系統框圖如圖4所示。其中，光學系統由全景環形光學鏡頭和濾光膜組成，濾光膜主要用來削弱進入光學鏡頭的光強，防止CMOS圖像傳感器工作于飽和狀態。設計中選用XILINX的spartan3A FPGA控制圖像傳感器行列時序，利用其內部的雙口RAM對每一行圖像數據進行緩沖，同時FPGA完成對光斑質心的求解。綜合考慮傳感器模型及標定算法的復雜程度，本設計選用C8051F340單片機實現質心坐標和角度信息之間的轉換及對圖像傳感器的初始化。該單片機工作時鐘可達48 MHz，能保證算法實現的實時性要求，同時，設計中我們采用單片機的串口作為該太陽敏感器的標準輸出接口，用來傳輸太陽角度信息或者壓縮后的圖像數據。此外，C8051F340內部具有USB2．0的高速接口，為了調試方便，我們利用該接口來實現調試階段的非壓縮BMP圖像數據傳輸。

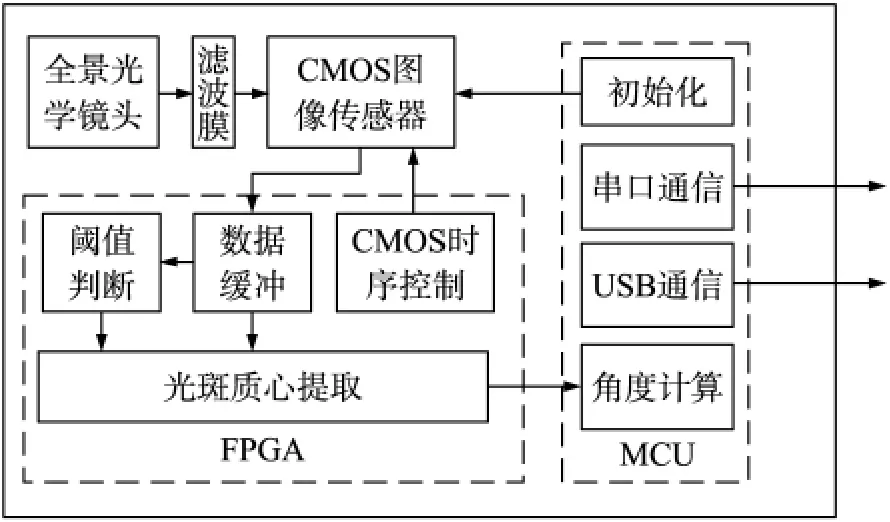
圖4 本文設計的太陽敏感器系統框圖

2．1 光學系統

光學系統選用的是浙江大學現代光學儀器國家重點實驗室設計的環形全景光學鏡頭，外形結構如圖5所示。

圖5 本文研究的全景環形光學鏡頭外觀

光學系統中選用巴德膜作為濾光膜，實驗證明，巴德膜配合光學鏡頭能夠有效地減弱太陽光強，濾除其他雜光干擾，使得所成太陽光斑像清晰、規則且亮度均勻。成像效果如圖6所示。

圖6 濾光膜下太陽成像效果

2．2 圖像傳感器

圖像傳感器選用 OmniVision公司型號為OV2640的 CMOS圖像傳感器[8]，OV2640 是一款高度集成的低電壓CMOS圖像傳感器，最大分辨率為1 600×1 200，單個芯片內集成了圖像傳感器和圖像處理器。OV2640提供了豐富的擴展功能，用戶通過SCCB(Serial Camera Control Bus)接口可以對傳感器進行配置，使其工作在不同模式。

OV2640支持多種圖像輸出格式，包括 RAW RGB、RGB、YUV等，同時，由于傳感器內部圖像壓縮模塊的存在，OV2640還支持JPEG格式壓縮圖像輸出。

在本設計中，綜合考慮太陽敏感器角度更新率和FPGA邏輯資源情況，我們將圖像傳感器配置在800×600分辨率的工作模式。

2．3 FPGA邏輯和單片機軟件

FPGA主要實現對OV2640的行列時序控制及光斑中心計算。與一些數字式太陽敏感器不同，本設計在FPGA內部加入了亮度閾值自動判斷模塊，在對光斑中心求解的同時，計算出當前幀的亮度信息，作為下一幀的亮度閾值。這種設計方法可以減輕單片機軟件工作量，使其工作方式簡單化，并能有效提高敏感器的更新率。

為方便圖像數據處理，在FPGA內部開辟兩塊大小為8×1 024 bit的雙口ram，交替對每行圖像數據進行緩沖。在利用緩沖區A進行圖像數據緩沖的同時，質心求解模塊和自動閾值計算模塊對緩沖區B的數據進行處理，即常見的乒乓操作方式。

FPGA內部核心模塊連接關系如圖7所示。其中，cmos_ctrl模塊實現對圖像傳感器行列控制，并緩沖圖像數據;data_proc模塊對cmos_ctrl緩沖區內的數據進行自動閾值判斷和采用質心法[9－10]對質心求解，同時cmos_ctrl模塊還完成與單片機之間的數據交互。

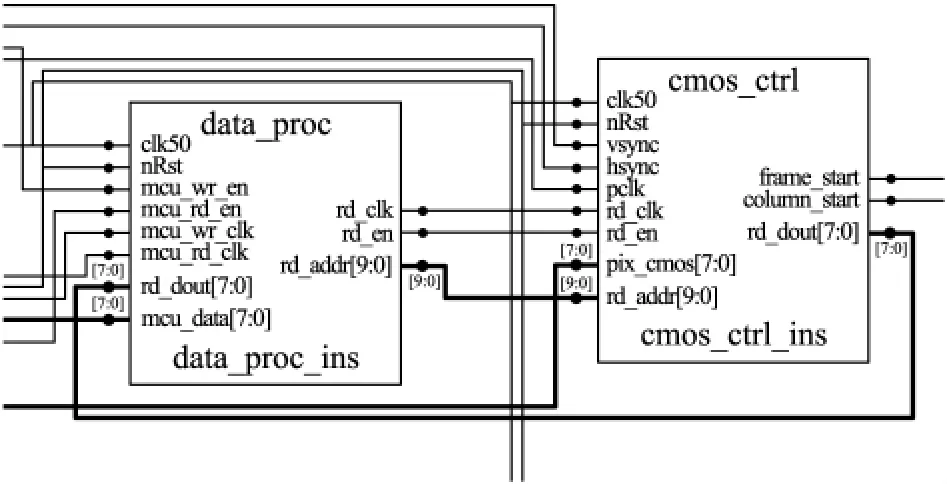
圖7 FPGA核心模塊關系圖

單片機軟件主要完成光斑中心坐標和太陽角度之間關系轉換、與上位機數據通信和圖像傳感器的初始化工作。在敏感器開始工作時，先由單片機對OV2640進行初始化，初始化完畢后，由于FPGA負責亮度閾值信息的判斷，單片機只需根據FPGA提供的過閾值亮點計數值來判斷是否捕獲到太陽位置，若捕獲成功，則輸出太陽角度信息有效。另外，我們還利用單片機自帶的高速USB接口，進行圖像傳感器原始圖像的傳輸，實現敏感器研制前期光學鏡頭安裝位置粗調及軟件算法的調試。

系統設計主要指標:

體積 55 mm×55 mm×50 mm;

質量 250 g;

功耗 300 mW;

最大更新率 30 Hz。

3 標定與測試

3．1 敏感器真實模型

敏感器模型本質上是一組描述太陽光斑中心坐標和太陽矢量之間關系的數學表達式。實際應用中的敏感器模型，與§1．3中介紹的敏感器成像原理相比，要更為復雜。式(4)、式(5)只是簡單地建立了光斑中心坐標和太陽矢量之間的關系，此關系通常只在理想情況成立。在真實情況下，諸如光學鏡頭安裝偏差、設計誤差等因素都需要考慮。

在本文研究的太陽敏感器模型中，安裝引起的偏差成為我們建立該模型主要考慮的因素[11－12]，主要包括:

(1)光軸與像平面中心之間的偏差(x0，y0)。

圖8 中心點偏差示意圖

(2)像平面X軸與安裝軸之間的角度偏差α0。

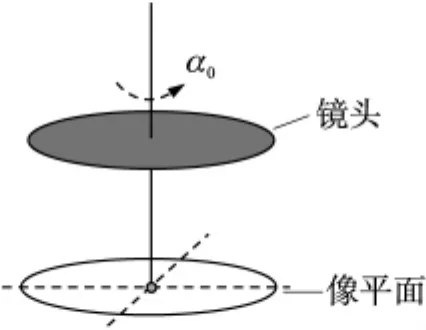
圖9 坐標軸安裝偏差示意圖

(3)光軸與傳感器安裝平面法線的角度偏差 β0。

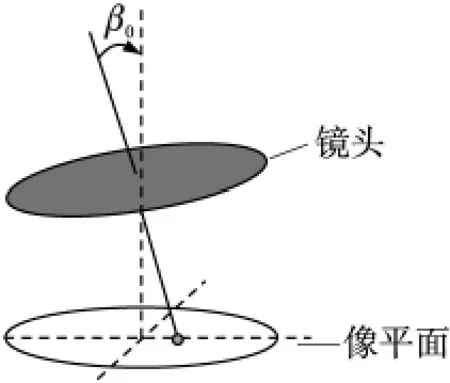
圖10 光軸安裝偏差示意圖

(4)光學鏡頭的焦距設計偏差f0。

綜合考慮以上4點，我們可以得到如下傳感器模型:

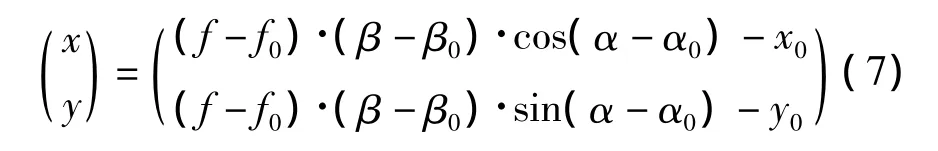
在上述傳感器模型中，存在5個參數需要確定，分別為 f0、α0、β0、x0和 y0。確定模型參數的方法在數據標定時比較常見，具體思路為:分別改變角度α和β，敏感器通過“質心法”計算得到光斑質心坐標的觀測值(xo，yo)，并通過串口將該坐標發送至PC端上位機軟件。將角度信息(α，β)代入式(7)所描述的傳感器模型可以得到光斑中心的坐標值(x，y)。假設角度(α，β)集合個數為N，則我們可以采集到N組光斑中心坐標觀測值(xo，yo)，并且根據模型可以計算得到N組光斑中心坐標(x，y)。

在采集完N組光斑坐標信息后，通過MATLAB等工具，尋求最優解，使得坐標集合(x，y)和(xo，yo)之間距離平方和最小，就可以確定模型中的5個參數。損失函數為:

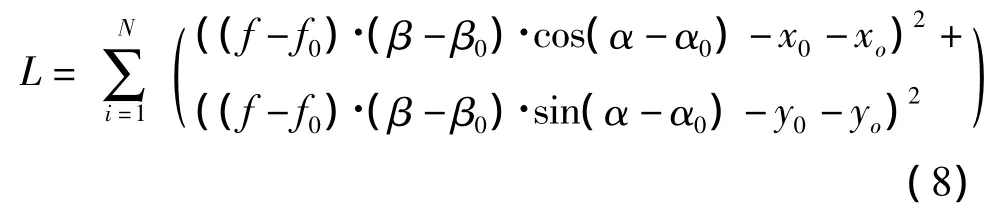
確定傳感器模型參數之后，可以根據式(9)計算太陽角度信息。

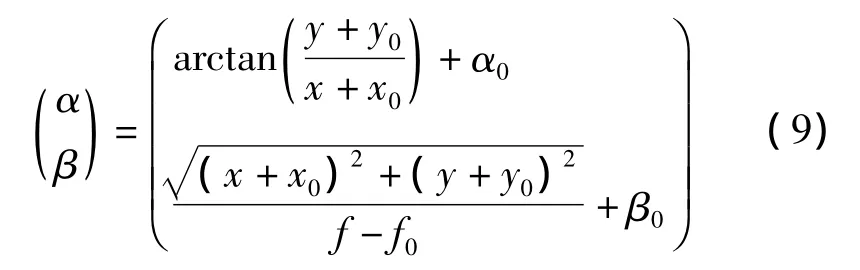
3．2 標定測試平臺

實驗平臺的搭建是傳感器精度標定的基礎。本文設計的實驗平臺主要由LED光源、高精度雙軸轉臺及精度標定軟件組成。測試時，PC端軟件通過串口控制雙軸轉臺，使其轉到設定的角度位置，待轉臺穩定后，軟件通過與傳感器之間通信獲取光斑中心坐標信息，并將其存檔。考慮到精度標定需要采集大量數據，因此我們在測試軟件中添加了自動測試工作模式，即只要設置好兩個軸的角度步進值后，軟件即可自動完成所有實驗，從而提高測試效率。實驗平臺實物圖如圖11所示。

圖11 實驗平臺實物圖

值得我們注意的是，如圖12所示，轉臺繞X軸旋轉后的角度β值與實際LED光源與傳感器光軸之間的角度β'并不完全一致。兩者之間存在如下關系:

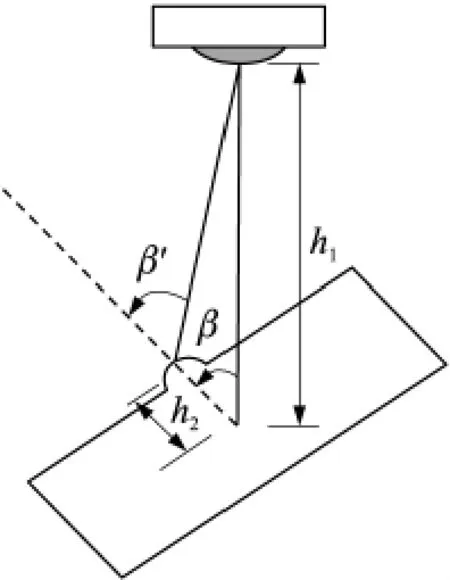
圖12 光源－傳感器光軸角度偏差示意圖

其中，h1、h2分別為LED光源和全景環形鏡頭到轉臺外框轉軸的距離。在實際對太陽敏感器進行精度標定時，需用由式(10)轉換后的 β’代入式(7)來計算光斑的中心坐標。

3．3 傳感器模型參數確定及精度測試

傳感器模型參數標定實驗中，首先在傳感器測量的兩個角度上以一定間隔進行取點[13]。角度β在范圍[－90°～ －30°]及[30°～90°]內，以 8°為間隔，角度 α 在范圍[－90°～90°]，以8°為間隔進行采樣點選取，共取得約300個采樣點。

根據式(8)及得到的采樣點，我們利用MATLAB的lsqnonlin函數來對之前建立的這個非線性模型進行最小均方最優解求解，得到式(7)模型中的5個參數分別如下:

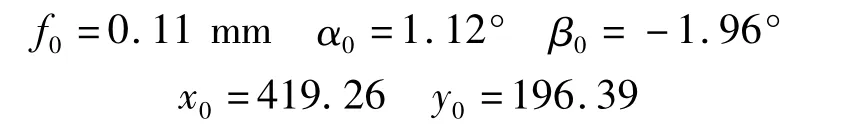
該組參數所對應的殘差為0．24像素點，與此像素點等效的角度測量精度為0．4°左右，誤差如圖13。

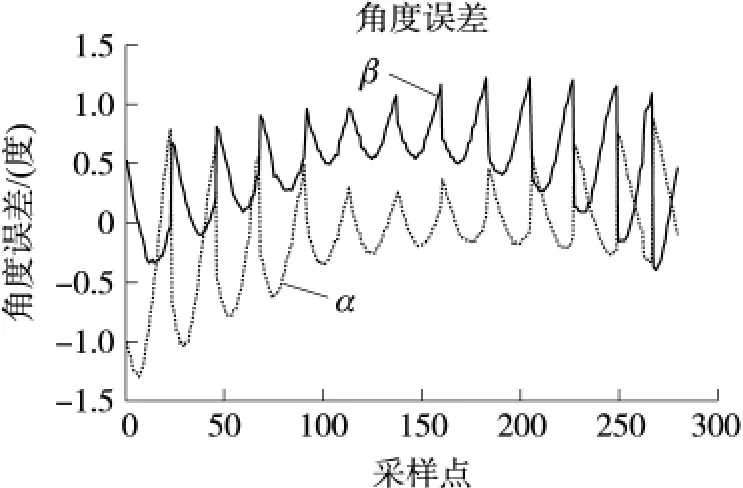
圖13 原始數據角度測量誤差

圖中實線部分是角度β測量誤差，虛線部分是角度 α 測量誤差，其數值分別為0．38°和0．43°。由圖13我們可知，測量值存在較為明顯的系統誤差。我們發現，對于固定的入射角β，其角度測量誤差會隨著α值的改變而變化，并具有明顯規律。經分析，我們得出此系統誤差主要是由太陽敏感器未安裝在轉臺中心引起的，仿真結果也很好驗證了這一結論。為了直觀得到本設計研制的太陽敏感器精度，我們對這一系統誤差作了補償。補償后角度β和α的測量誤差值都為0．02°，與補償前相比有很大提高。同時，為了說明此補償效果，我們對該太陽敏感器的測量穩定度進行了一組實驗，即采集同位置下的角度信息，觀察其輸出波動。實驗結果顯示，該太陽敏感器的輸出穩定度約為0．009°，與之前補償后的輸出誤差較為接近，表明補償效果理想，能真實反映敏感器的測量精度。圖14為補償后的角度測量誤差。

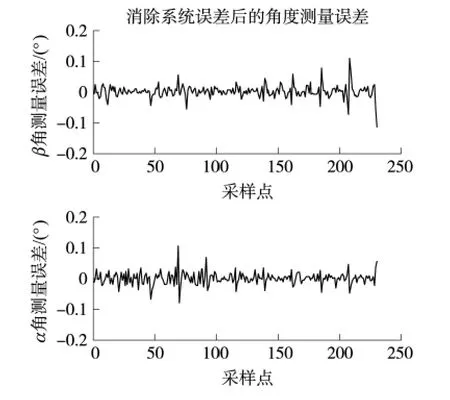
圖14 補償數據角度測量誤差

4 結論

測試結果表明，本文設計的太陽敏感器具有120°×180°的大視場，且在該視場范圍內誤差分布均勻，一致性較好，同時，采用本文提出的標定方法標定后，其測量精度達到0．02°，與普通單孔掩膜式數字太陽敏感器基本一致[11]，符合設計要求。

該太陽敏感器可主要用于對視場要求高，精度要求一般的衛星姿態確定系統。同時，由于算法上的精簡，使得該敏感器硬件結構簡單，從而有效降低了系統功耗、減小了系統體積和質量，特別適合作為皮衛星等微小衛星的姿態確定傳感器。

[1]賈傳良．數字式太陽敏感器研究[D]:[碩士學位論文]．哈爾濱:哈爾濱工業大學控制科學與工程系，2007．

[2]何麗，胡以華．太陽敏感器原理技術發展淺析[J]．傳感器世界，2006(1):12－14．

[3]陳凡勝．大視場高精度太陽敏感器的實現[J]．紅外，2004(9):10－15．

[4]樊巧云，江潔，張廣軍．小型CMOS太陽敏感器[J]．光電工程，2007，34(2):133 －136．

[5]Chen F F，Feng J，Hong Z W．Digital Sun Sensor Based on the Vernier Measuring Principle[J]．Measurement Science and Technology，Institute of Physics Publishing，2006(17):2494 －2498．

[6]程惠全，姚煒勇，楊國光，等．全景環形成像的轉像系統設計[J]．光電工程，2002，29(2):16 －19．

[7]侯惠杰．全景環形成像展開算法的研究[D]:[碩士學位論文]．浙江:浙江大學信息學院，2006．

[8]李輝，張鈺，楊牧，等．基于 CMOS圖像傳感器的皮衛星成像系統設計[J]．傳感技術學報，2010，23(1):62 －67．

[9]楊清珍，陳朝陽，沈緒榜，等．用FPGA實現星圖目標的質心提取[J]．計算機與數字工程，2005，33(10):63 －65．

[10]Chang Y K，Kang S J，Lee B H ．High-Accuracy Image Centroiding Algorithm for CMOS-Based Digital Sun Sensors[J]．IEEE Sensors，2007:329－336．

[11]Carl Christian Liebe，Sohrab Mobasser，Youngsam Bae，et al．Micro Sun Sensor[C]//IEEE Proceeding Aero Space Conference，Piscataway NJ IEEE，2002(5):2263 －2273．

[12]John P Enright．Design Optimization of a Digital Sun Sensor for Use With Parametric Processing[J]．IEEE Transaction On Instrumentation and Measurement，2008，57(10):2188 －2195．

[13]John Enrighta，Doug Sinclairb，Chris Li．Embedded Algorithms for the SS-411 Digital Sun Sensor[J]．Acta Astronautica，2009(64):906－924．