費馬大定理的一種證明方法

饒世麟，饒雪梅，饒雪芳

(1.軍委總裝備部北京第10干休所，北京 100101;2.中國聯通公司國際部，北京 100033;3.北京跟蹤與通信技術研究所，北京 100094)

費馬大定理是一個困惑世間智者358年的問題，于1994年被英國數學家Andrew J.Wiles用現代數學攻克。本文則通過驗算，提出了一個與費馬大定理有關的猜想，即R猜想:若正整數m＞2，c，d為正整數且cd≠0)，則不定方程

1 R猜想的證明

首先作者通過多次計算機驗算，發現了定理1。定理1 設正整數m＞2，無論m=4n，2n或奇數，c、d均為不等于0的正整數，則一元二次方程式

沒有整數解。其判別式為

1.1 預備知識

根據文獻［1］有

引理1 (Perron判別法)，設a(0)≠0

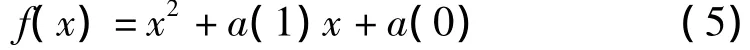
引理2 若a≠0，2次整系數一元方程式

僅當a=4且為x2±4x+4=0時才有整數解。

根據文獻［1］有

引理3 若uvw≠0，k＞1，(u，v)=1。則方程式 uv=wk，有正整數解為 u=ak，v=bk，w=ab，(a，b)=1。

根據文獻［2］有

引理4 若正整數m＞2，則xm－ym=1，沒有正整數解。

1.2 定理的證明

(2)若c=d。方程式(3)寫為

因為m＞2，cm≠4，根據引理2，方程式⑺沒有整數解，定理成立。

(3)若c＜d。這時有以下幾種情況:

1)c=1，d=t，其中t為大于1的任何正整數。

于是式(3)變換為

設式(8)有整數解x1及 x2，則

由式(10)知，必有(x1，x2)=1。根據引理3，有 x1= ±，x2= ±，t=t1t2，(t1，t2)=1。代入式(10)中得+=±1。這顯然不可能，即使把左邊的“+”號改成“－”號，根據引理4也是不可能的，所以式(8)沒有整數解，判別式整數。定理成立。

2)c＞1，且d=c2t，其中t為任何正整數。

則式(3)變換為

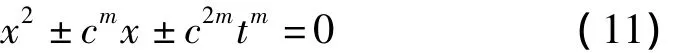
3)c＞1，且(c，d)=1。

此時式(3)的形式不變，即

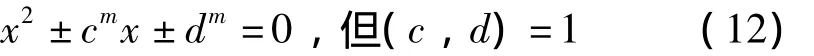
4)c＞1，(c，d)=e≠1，且 e2⊥d，其中⊥表示不整除。

令c=ec'，d=ed'，則式(3)變換為x2±emc'mx±emd'm=0，若此方程有整數解，則可令 x=emy，則e2my2±emc'memy±emd'm=0，即 y2±c'my±

因e2⊥d，e⊥d'，第3項只能是既約分數，而不是整數，所以方程式沒有整數解。于是式(3)也沒有整數解，定理成立。

令 c=ec'，d=e2d″，則式(3)變換為 x2±emc'mx±e2md″m=0，若此方程式有整數解，則可令x=emy，則此方程式變換為，y2±c'my±d″m=0 但(c'，d″)=1，此方程式與式(12)類似。所以此方程式和方程式(3)都沒有整數解，定理成立。

綜合以上情況，即不論c＞d，c=d或c＜d，定理都成立。

1.3 定理的舉例

下列一元二次方程式都沒有整數解。

(1)c＞d的情況，x2+33x－23=0，其判別式為

(2)c=d的情況，x2+25x+25=0，其判別式為

(3)c＜d的情況，x2+24x－34=0，其判別式為

2 費馬大定理的證明

費馬大定理:若正整數m＞2，xyz≠0，則方程式xm+ym=zm沒有整數解。

若R猜想不成立，由式(1)有c2m=4dm+s2，令s=am－bm，d=ab，則(cm)2=4(ambm)+(am－bm)2=(am+bm)2，即 cm=am+bm，因此費馬大定理不成立。

同樣，由式(2)有c2m=s2－4dm，令s=am+bm，d=ab，則(cm)2=(am+bm)2－4(ambm)=(ambm)2，即cm=am－bm，因此費馬大定理不成立。

若R猜想成立，則式(1)和式(2)均沒有正整數解。變量s，d，c不能同時都為整數，因此cm=am+bm和cm=am－bm都不能出現，因此費馬大定理成立。

綜上所述，有:“若R猜想不成立……因此費馬大定理不成立。”這說明R猜想是使費馬大定理成立的必要條件;又有“若R猜想成立……因此費馬大定理成立”，說明R猜想是使費馬大定理成立的充分條件。二者結合，說明R猜想是使費馬大定理成立的充要條件，證畢。

3 費馬大定理與R猜想的等效性

上面利用R猜想證明了費馬大定理，其實，反過來也可利用費馬大定理證明R猜想。

若費馬大定理不成立，令cm=am+bm，d=ab代入式(1)中有(am+bm)2－4(ambm)=s2即 s2=(ambm)2，s=am－bm，故式(1)有正整數解，R猜想不成立。

同樣，令cm=am－bm，d=ab代入式(2)中有(am－bm)2+4(ambm)=s2即 s2=(am+bm)2，s=am+bm，故式(2)有正整數解，R猜想不成立。

若費馬大定理成立，就不能令cm=am+bm或cm=am－bm，故式(1)與式(2)都沒有正整數解，R猜想成立。

所以，費馬大定理是使R猜想成立的充要條件，即利用費馬大定理證明了R猜想。

綜上所述，費馬大定理與R猜想是等效的。是同一真理的兩種不同的表現形式。

4 結束語

文中構成了一種運用初等數論證明費馬大定理的簡明方法，這種方法與國際上運用現代數論證明費馬大定理的方法［3］，形成了鮮明對比。

［1］ 柯召，孫琦.數論講義:2冊［M］.北京:高等教育出版社，1990.

［2］ 柯召，孫琦.談談不定方程［M］.上海:上海教育出版社，1980.

［3］ 張賢科.古希臘名題與現代數學［M］.北京:科學出版社，2007.