LTE上行信道估計技術研究

盛洪寧

(西安電子科技大學電子工程學院，陜西西安 710071)

LTE(Long Term Evolution)系統最大的改進在于采用了全新的空中接口技術，上行采用SC－FDMA多址接入技術，下行采用 OFDMA(Orthogonal Frequency Division Multiple Access)技術。SC－FDMA是結合OFDM可動態分配帶寬的單載波多址接入方案，相對于OFDM技術，SC－FDMA系統的功率峰均比更低，有利于節省終端的成本和功率以及提高上行鏈路的覆蓋范圍［1－3］。

LTE上行的用戶數據和控制信息主要是通過PUSCH(Physical Uplink Shared Channel)承載。PUSCH采用了塊狀參考信號結構，在一個子幀中插入2個導頻符號。受到無線信道的時變特征、多徑衰落和多普勒頻移的影響，eNodeB接收到的往往是嚴重失真信號。因此，準確的信道估計是保證PUSCH傳輸質量、發揮其優越性的關鍵［4－6］。

本文將重點研究基于輔助導頻的PUSCH信道估計技術，信道估計分為兩個基本步驟:首先，估計出導頻位置的信道響應;然后，根據導頻位置的信道響應，運用插值算法恢復出全部數據位置的信道響應。衡量信道估計算法的優劣，主要考慮算法的復雜度和估計精度，目標是實現低復雜度的同時獲得較好的估計性能。

1 LTE PUSCH傳輸方案

PUSCH采用了DFT－S－FDMA(Discrete Fourier Transform－Spread－FrequencyDivisionMultiple Access)技術。DFT－S－FDMA主要思想是數據在OFDM調制前，先進行DFT變換的預編碼，實現了單載波的傳輸方案［7－8］。

如圖1所示，在PUSCH基帶調制過程中，輸入的比特是經過信道編碼的碼字。首先，碼字進行調制映射，生成復數符號 d=［d0，d1，…，dM］T，PUSCH支持多種調制方式，有 QPSK、16QAM和64QAM。然后，調制后復數符號進行M點DFT變換，得到 X(k)，k=1，2，…，M。將 M點頻域數據X(k)映射到相應的在載波資源上，并在一個子幀的第4和第11個符號插入導頻序列。再進行N點IFFT變換，生成N點采樣點x(k)。N與系統帶寬有關，如系統為10 Mbit·s－1帶寬時，N=1024。最后經過添加循環前綴、串并轉換和數模轉換，天線發射。

接收到的頻域數據Y=［Y1，Y2，…，YNP］，可以表示為

其中，h(k)是信道的離散響應，其頻域響應為H;w(k)是加性噪聲干擾，其頻域響應為W;Np是導頻長度，也是UE的子載波的個數;X=［X1，X2，…，XNP］是發射端頻域數據和導頻信號。信道估計的目的就是要獲取信道的頻域響應H。

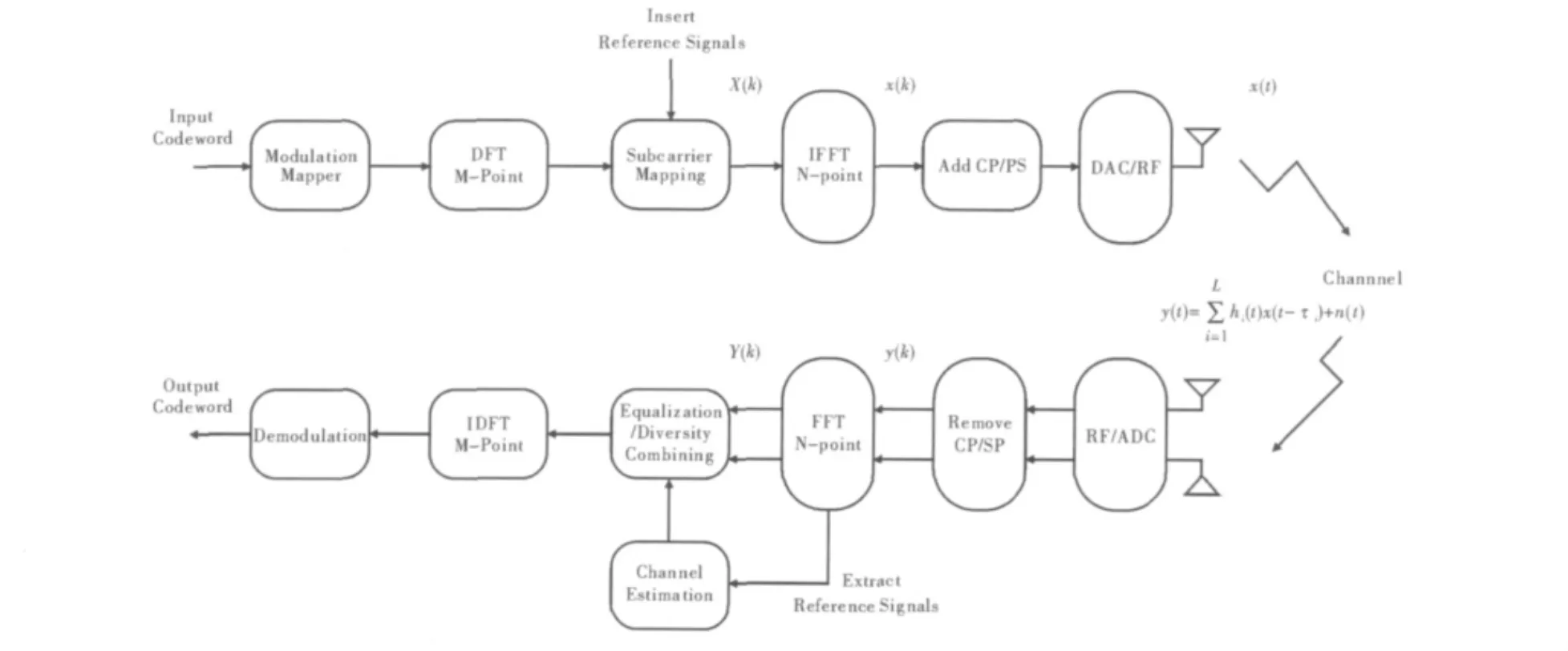
圖1 PUSCH傳輸方案框圖

PUSCH的導頻結構如圖2所示。黑色部分表示的是PUSCH導頻信號的分布，頻域上占據整個帶寬，時域占用一個 Slot中 l=3的 SC－FDMA符號。PUSCH的參考信號分布是典型的塊狀導頻結構，相對于其他的導頻結構，塊狀導頻結構特別適用于慢衰落信道的無線信道。在頻域上導頻覆蓋了所有的子載波，因此頻域上無需插值。

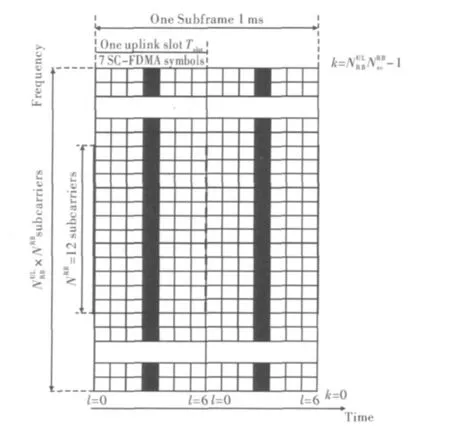
圖2 LTE上行Subfarme的時頻結構和參考信號(黑色部分)

實際上，接收端的過程要比發射端復雜得多，涉及到時間和頻率同步、信道估計、均衡、分集合并和數據解映射等諸多關鍵技術。這里，假設在時頻同步是理想情況下，進行信道估計研究。

2 信道估計

根據估計準則的不同，基于導頻的信道估計方法常見有兩種，最小二方差LS和最小均方誤差MMSE算法。下面分別對這兩種算法進行分析。

2.1 基于LS估計準則算法

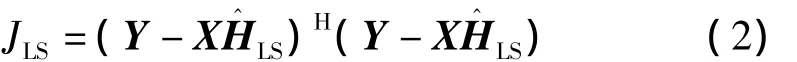
式中，Np表示參考信號的長度。根據代價函數最小準則，使JLS=0，得到

可見，頻域LS信道估計方法算法簡單，易于實現，因此得到廣泛應用。但是，由于LS準則并沒有考慮到噪聲的影響，信道估計的結果將受到噪聲的嚴重影響。如式(4)所示

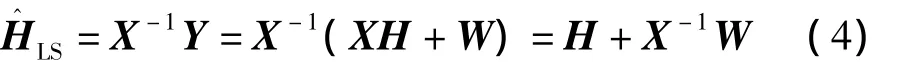
LS信道估計沒有考慮噪聲W的影響。因此，LS雖然算法復雜度低，實現簡單，但是估計的誤差較大，信道估計精度較低。

2.2 基于MMSE估計準則算法

為提高信道估計的精度，根據維納濾波器理論［1］，希望通過濾波器得到信道響應

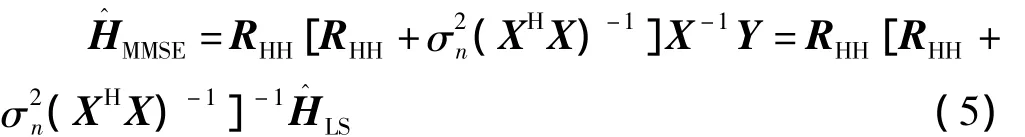
從式(5)可知，MMSE(Minimum Mean Square Error)估計方法實際上是對LS初估計結果進行一次濾波得到的信道估計。MMSE估計準則算法，是在最小均方誤差意義上的最佳估計方法，精度較高。但是，這樣的MMSE算法計算復雜度高，涉及到多次NP×NP復數矩陣的乘法和求逆，因此難以在實際系統中應用。

這里，對MMSES算法進行簡化。首先，式(9)中的(XHX)－1，實際上導頻信號可以確定，不需要實時計算導頻信號的變化。根據3GPP TS36.211協議的定義，導頻序列實際上是BPSK調制的信號，因此幅值這樣，就有恒定(XHX)－1=1。由于功率控制的需要，(XHX)－1=，等于信號的發射功率，則有

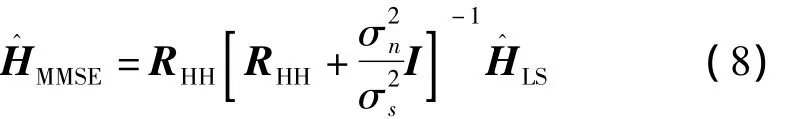
由信道的相關性特征可知，信道的自相關矩陣RHH=［rf(k1，k2)］由多徑衰落的功率和時延決定，其時延功率譜服從負指數分布，一般相隔較遠的子信道的相關小，與當前子信道鄰近的自信道相關性較大。即頻域上頻率間隔較遠的子載波相關性很小，頻域上鄰近的子載波相關性稍大。因此，可以對信道的自相關矩陣進行簡化。

式(8)中，RHH=E［HHH］是一個NP×NP的矩陣

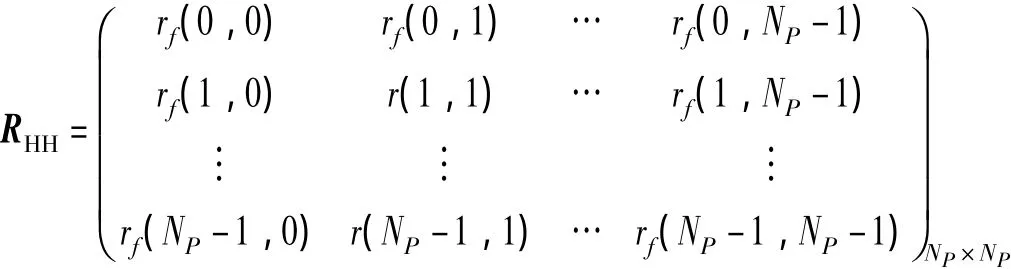
從R'HH矩陣可以看到，簡化后的算法復雜度將大大降低。尤其當NP較大時，簡化的運算量將是很大，原來一次矩陣乘法運算需要NP×NP次復數乘法運算，簡化后只需要NP×L次，這樣一次復數矩陣乘法運算就減少了NP×(NP－L)次乘法運算。

在實際應用中，經過簡化的信道自相關矩陣RHH和噪聲功率，可以通過實時測量獲取，或者是根據真實信道的統計特性通過假設的方式預先確定，這樣只需要一次乘法運算即可完成MMSE的計算。

在取得導頻位置的信道估計值后，進而通過插值方法恢復出全部的數據位置的信道響應。常見的插值算法一階線性內插性、二階拋物線內插和基于DFT的插值方法等，不再贅述。

3 仿真結果及性能分析

本文仿真的LTE PUSCH參數配置如表1所示。這里對系統中的某個用戶進行估計，該用戶的上行資源為12個PRB。信道采用WSSUS信道模型，為廣義平穩的多徑時變瑞利衰落信道，6條多徑的功率延遲譜服從負指數分布。

表1 系統仿真參數

信道估計算法性能的衡量指標是估計的均方誤差MSE(Mean Square Error)和誤符號率 SER(Symbol Error Rate)，采用蒙特卡洛仿真方法，得到的仿真結果如圖3和圖4所示。

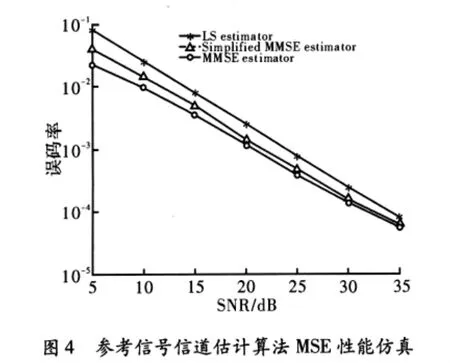
如圖4所示，簡化后的MMSE算法的誤碼率SER性能非常接近理想的MMSE算法性能，明顯優于基于LS算法。例如在SNR=8 dB時，簡化MMSE算法的誤符號率比LS算法的SER約低10 dB，與MMSE算法相差約1 dB。同樣，如圖5所示，LS估計算法和MMSE估計算法在MSE性能上有較大的差距。顯然，簡化MMSE算法的估計精度接近MMSE算法，并明顯優于基于LS準則的信道估計。

4 結束語

基于上述分析和仿真結果，簡化算法用的整體性能優異，達到系統性能與復雜度的折衷。對于LTE PUSCH接收機信道估計，適于采用簡化MMSE算法。該在實際應用中，信道的相關矩陣RHH和噪聲功率可以通過實時地跟蹤信道獲取，也可以通過大量的真實信道的測量和仿真后設定為一個或一組固定值，這樣較大程度地簡化了運算過程，易于實現。

［1］ SIMON HAYKIN.Adaptive filter theory［M］.3rd Ed.New Jersey:Prentice Hall，Englewood Cliffs，1996.

［2］ JAN －JAAP VAN DE BEEK，OVE EDFORS，MAGNUS SANDELL，et al.On channel estimation in OFDM system［C］.Chicago:45th IEEE Vehicular Technology Conference，1995，2:815－819.

［3］ 中興通訊股份有限公司.3GPP TS 36.211 V870(2008－6)，3GPP TSG RAN E－UTRA Physical Channels and Modulation(Release 8)［S］.深圳:中興通訊股份有限公司，2008.

［4］ 中興通訊股份有限公司.3GPP TS 36.212 V870(2008－6)，3GPP TSG RAN E－UTRA Multiplex and Channel Coding(Release 8)［S］.深圳:中興通訊股份有限公司，2008.

［5］ 曾召華.LTE基礎原理與關鍵技術［M］.西安:西安電子科技大學出版社，2010.

［6］ 沈嘉，索士強，全海洋，等.3GPP長期演進(LTE)技術原理與系統設計［M］.北京:人民郵電出版社，2009.

［7］ 王軍選.多徑相關衰落下影響LTE系統容量因素分析［J］.現代電子技術，2011(3):36－38.

［8］ 許寧，蔣峰，徐凱.3GPP LTE小區間干擾協調方案研究［J］.現代電子技術，2007(21):57－60，77.