改進的混合蛙跳算法求解背包問題

陳 亮

(泰山職業技術學院信息工程系，山東泰安 271000)

0 引 言

混合蛙跳算法(shuffled frog leaping algorithm，SFLA)是2000年由Eusuf和Lansey受青蛙群體覓食的行為啟發，并總結其規律而提出的一種基于群體智能的后啟發式仿生算法[1]。該算法將全局信息交換和局部深度搜索相結合，通過局部搜索使得信息能在局部個體間傳遞，其采用的混合策略能使得局部信息在全局范圍內得以傳遞[2]。

1 背包問題

背包問題(knapsack problem)是一種組合優化的NP完全問題，通常背包問題分為0/1背包問題、完全背包問題、多重背包問題、混合背包問題4種，由于后3種可以轉化為第一種，因此，文中只討論0/1背包問題[3]。

0/1背包問題的數學模型描述為:

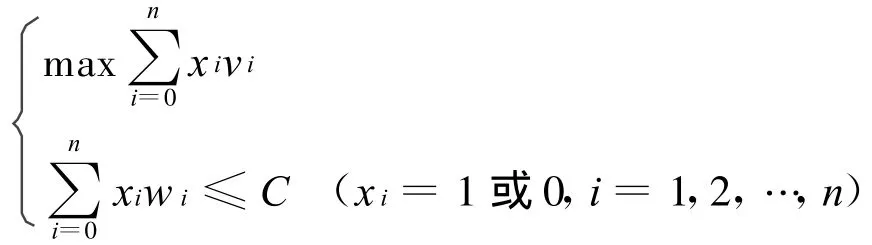
式中:n——物體個數;

w i——第i種物品的重量(i=1，2，…，n);

vi——第i種物品的價值;

xi——第i種物品的選擇狀態，當物件i被選入背包時，定義變量xi=1或0;

C——背包的最大容量。

2 混合蛙跳算法基本流程

隨機生成P只青蛙，每只青蛙代表一個問題的解，記為Ui，并視為初始族群。然后計算族群內所有的青蛙的適應度，并將青蛙按適應度降序排列，再將整個族群內的青蛙分成m個子族群，每個子族群包含n只青蛙，因此滿足關系P= m*n。分配方法:按排定順序把第1，2，…，n只青蛙分別分到第1，2，…，n個子族群中，第a+1只青蛙分到第1個子族群中，依次類推，直至全部青蛙分配完畢[4]。

對于每一個族群，設UB為適應度最好的解，UW為適應度最差的解，U g為所有族群中具有全局最好適應度的解。然后對每個族群進行局部深度搜索，并對局部最優解進行更新，更新策略為[5]:

式中:S——青蛙個體的調整矢量;

S max——青蛙個體允許改變的最大步長;

rand——0和1之間的隨機數。

3 基于混合蛙跳算法的0/1背包問題求解

3.1 青蛙個體向量表示

一只青蛙代表一個解，用物體選擇狀態向量表示，則青蛙U=(x1，x2，…，xn)，其中xi表示第i個物體的選擇狀態。即xi=1，表示選中第i個物體;xi=0，表示未選中第i個物體。青蛙個體適應度函數f(i)定義為:

3.2 子族群的構造

在構造子族群時，根據適應度的大小進行青蛙選擇，即適應度較大，選擇權重越大，越有機會選中加入到子族群中。按概率選擇青蛙進行子族群的構造，概率公式定義為[6]:

且

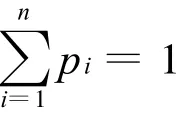
式中:pi——第i只青蛙被選中的概率;

n——每個族群中青蛙個數。

3.3 青蛙個體的更新策略

定義1 給定一個青蛙向量U，定義交換序C(i，j)為:

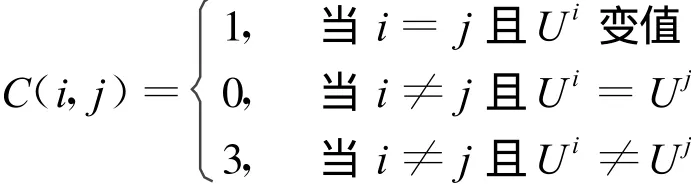
式中:Ui變值 ——物品i由選中狀態變為取消狀態，或相反;

Ui=Uj——物品i與物品j交換位置，即物品i與物品j同為選中或取消狀態;

Ui≠Uj——選中物品i且取消物品j，或相反。

則交換操作的新向量

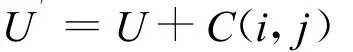
定義2 在族群中任意選兩只青蛙的向量Ui，U j，由U i調整到U j的所有交換序列稱為U i到U j的距離D:

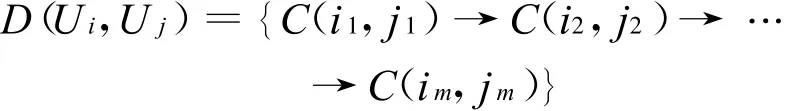
式中:m——調整的次數。

定義3 在族群中任意選兩只青蛙的向量Ui，U j，由U i調整到U j的距離長度為|D|

式中:m——調整的次數。

由以上定義確定青蛙個體的更新策略如下:

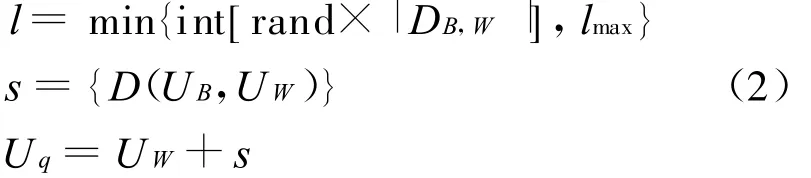
式中:l——更新UW選擇用交換的D(UB，UW)交換序的個數;

lmax——允許選擇的最大交換序的個數;

s——更新UW所需的交換序列。

3.4 全局信息交換策略

在基本混合蛙跳算法執行過程中更新可行解的操作反復被執行，不可避免地遇到更新失敗的情況，基本的混合蛙跳算法采用了隨機更新可行解的方法，但隨機方法經常會陷入局部最優或使算法的收斂速度降低。文中引入高斯變異算子以修正更新策略，即用高斯變異算子對子族群最差青蛙(可行解)進行擾動，即:

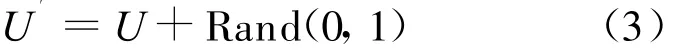
式中:Rand——高斯隨機分布函數。

新的更新策略在整個迭代過程中將提高群體的多樣性和最差個體搜索的遍歷性，可以確保群體持續進化，有利于提高收斂速度，并避免陷入局部最優，進而期望算法既能快速收斂到最優解的附近，又能比較好地逼近精度，改進了混合蛙跳算法的性能。

3.5 算法描述

步驟1:初始化青蛙族群，并生成初始子族群。

步驟2:按式(1)計算每只青蛙的適應度，并按降序排序。

步驟3:搜索出全局最優可行解Ug、子族群最優可行解UB和最差可行解UW。

步驟6:更新完成后，對所有子族群的所有青蛙重新進行混合，形成新的族群。

步驟7:輸出Ug。

4 實驗結果分析

采用兩個經典0/1背包問題實例，實例1選自文獻[7]，實例2選自文獻[8]。采用的對比算法為0/1背包問題分支限界法。在相同實驗條件下對兩個實例分別進行20次仿真實驗，統計其平均實驗結果，見表1。

表1 實驗結果

經過分析實驗結果，兩種算法執行結果相同，混合蛙跳算法的執行速度有較大提高，因此，混合蛙跳算法是有效、可行的。

5 結 語

混合蛙跳算法是一種具有隨機智能和全局搜索能力的搜索算法，文中應用混合蛙跳算法解決了0/1背包問題求解。實驗證明，混合蛙跳算法在解決0/1背包問題上具有較好的可行性和有效性，采用高斯變異算子有效避免了易陷入局部最優的缺陷，在一定程度上提高了算法的收斂速度。

[1] 羅雪暉.改進混合蛙跳算法求解旅行商問題[J].通信學報，2009，7(7):130-134.

[2] 周麗娟.改進粒子群算法和蟻群算法混合應用于文本聚類[J].長春工業大學學報:自然科學版，2009，30(3):281-284.

[3] 吳哲輝.算法設計與分析[M].北京:高等教育出版社，1993:248-249.

[4] 羅雪暉.基于混合蛙跳算法的背包問題求解[J].科學技術與工程，2009，8(15):4364-4365.

[5] 駱劍平，李霞.求解TSP的改進混合蛙跳算法[J].深圳大學學報，2010，4(2):173-177.

[6] 欒壺琛.混洗蛙跳算法研究及其發展現狀[J].大眾科技，2009(1):24-26.

[7] 賀毅朝.求解背包問題的貪心遺傳算法及其應用[J].計算機工程與設計，2007，28(11):19-22.

[8] 吳哲輝.算法設計與分析[M].北京:高等教育出版社，1993:251-152.