讓數學原理寓于數學活動之中
——《商不變的性質》教學設計及反思

■馮勝 邵承民

讓數學原理寓于數學活動之中
——《商不變的性質》教學設計及反思

■馮勝 邵承民

《商不變的性質》是人教版課標教材小學數學四年級上冊第93頁的教學內容，是學生在知道積的變化規律、學習除數是兩位數的除法后，通過計算、觀察、比較、抽象以及概括等活動發現、歸納商不變的性質。這部分內容的教學不僅可以鞏固所學的計算知識，培養學生初步的抽象、概括能力以及探究能力，同時還能為學生以后學習小數除法以及函數知識做準備。

本堂教學設計，通過將數學原理寄于數學活動之中，讓學生經歷自主探究的過程，促進和深化了學生對數學思想方法的理解，幫助學生構建了“商不變的性質”這一數學知識，是一個較為有效的課堂教學。

【教學設計】

教學內容：人教版課標教材小學數學四年級上冊第93頁

教學目標：

1．讓學生經歷發現、抽象、概括商不變的性質過程，理解并會用這一性質解決有關問題。

2．在發現、歸納商不變的性質過程中，培養學生觀察、比較、抽象和概括的能力。

3．培養學生積極思考、勇于探索的學習習慣，感悟“形變值不變”的辨證唯物主義觀點。

教學重點：使學生理解商不變的性質，并能用這一性質解決有關問題。

教學難點：使學生發現并歸納概括商不變的性質。

教學關鍵：引導學生發現算式之間的變化規律，用數學語言進行較為準確的歸納、概括。

教學過程：

一、創設情境，導入新課

1．多媒體課件出示“猴王分桃”的場景，猴王說：“給你6個桃子,平均分給你們3只小猴吧。”小猴一想，連連搖頭說:“太少了，太少了。”猴王又說：“好吧,給你60個桃子,平均分給30只小猴，怎么樣?”小猴子得寸進尺,撓撓頭皮,試探地說:“大王，再多給點行不行啊？”猴王一拍桌子,顯示出慷慨大度的樣子:“那好吧,給你600個桃子,平均分給300只小猴,你總該滿意了吧。”小猴子覺得自己占了大便宜開心地笑了,猴王也笑了。

2．提出問題：你覺得誰是聰明的一笑？為什么？

3．學生自由回答：猴王的笑是聰明的一笑，按照這三種分法，每只小猴得到的都是2個桃子。

4．教師啟發思考：你是怎樣知道每次分的一樣多的呢？

5．學生匯報，教師板書：6÷3=2，60÷30=2，600÷300=2。

6．提出問題：觀察幾個算式，你發現了什么？

7．學生回答：這幾個除法算式的商都是2。

二、比較歸納，探究新知

1．引導發現。

（1）提出問題：大家觀察的真仔細，你還能說出幾道商是2的除法算式嗎？

（2）學生自由匯報，教師選擇板書：12÷6=2，24÷12=2，48÷24=2，6000÷ 3000=2，……

（3）引導思考：同學們說的真好！這些算式排的太亂，誰能把他們按一定的順序排列呢？

（4）學生回答，教師板書：6÷3=2，12÷6=2，24÷12=2，48÷24=2，60÷ 30=2，600÷300=2，6000÷3000=2。

2．提出問題。

比較每個算式的被除數、除數和商：①從上到下看，是按照什么規律變化的？②從下到上看，是按照什么規律變化的？

3．集體討論，歸納性質。

（1）學生小組討論。

（2）教師引導交流。

①教師引導學生交流：從上到下看，是按照什么規律變化的？

學生舉例說：6÷3=2到12÷6=2的變化規律。教師指出：像這樣的變化過程，我們可以說：6÷3=2被除數和除數都擴大2倍，商不變。

②追問：其他幾組算式的變化規律是怎樣的？你能歸納它們的變化規律嗎？

學生說出其他幾組的變化情況后，試著歸納變化規律：被除數和除數都擴大相同的倍數，商不變。

板書：同時擴大，相同的倍數。

③教師引導學生思考：從下往上看，又是按照什么規律變化的？

④學生舉例說明，引導學生通過分析比較算式中被除數和除數，得出：被除數和除數都縮小相同的倍數，商不變。

板書：同時縮小

（3）歸納性質。

①引導歸納：你們能把剛才我們發現的這兩個規律用比較簡潔的語言概括成一句嗎？

②學生交流：被除數和除數同時擴大（或縮小）相同的倍數，商不變。

③揭示性質：這就是商不變的性質，前面要“在除法中”就更好了。這就是我們今天學習的內容——商不變的性質。（板書課題：商不變的性質）

（4）理解性質。

①教師質疑：請同學們說一說這個性質中哪些字或詞比較關鍵，為什么？

②學生回答：同時，因為……；相同的倍數，因為……（板書作重點記號）

（5）回歸情境。

思考：猴王是運用了什么規律來分桃“忽悠”了小猴子的？

三、多層練習，深化新知

1．不計算，判斷下面哪個算式與“16÷8”的商是相等的？為什么？

（16×2）÷（8×2）

（16÷2）÷（8×4）

（16×4）÷（8×5）

（16＋2）÷（8＋2）

利用這些題目，引發學生的爭論，讓大家在爭論中加深對商不變性質的理解。

2．在○里填運算符號,在□里填數。

800÷25=(800×□)÷(25×4)

2800÷400=(2800÷100)÷(400 ÷□)

36÷18=(36○□)÷(180○□)

在學生填數的基礎上,引導發現“0除外”,完善對“商不變的性質”的理解。

3.根據3120÷260=12，很快說出下面各題的商。

312÷26=

31200÷2600=

1560÷130=

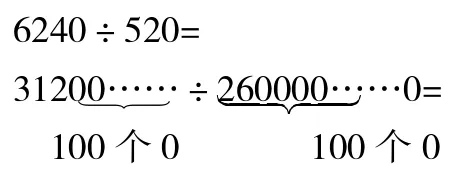
讓學生利用“商不變的性質”靈活地簡化計算。

四、課堂小結，延伸質疑

1．通過學習，你有什么收獲？

2．你能舉出一些商不變的性質在生活中的應用嗎？

3．下課后，請手里卡片上算式得數與“28÷7=4”的得數相等的同學先出教室。（課前先發了一些寫有除法算式的卡片）

【教學反思】

樸素而豐富的數學原理“商不變的性質”怎樣從學生大腦中生長出來呢？本節課進行了一些嘗試，并有了以下三點感悟：

一、探究欲望源于興趣的激發

課堂應是點燃學生智慧的火把，恰到好處的問題情境，可以暴露學生認識中的矛盾，激發學生的學習興趣，引發學生探究知識的欲望。在本節課，一開始教師先出示“猴王分桃”的趣味情境，講述了一段生動的故事，學生非常感興趣，并立即被吸引，從而認真思考故事中提出的問題。通過故事設疑，激發了學生探究新知的欲望，為后續學習做好了心理準備。

二、知識生長源于有效的建構

建構主義對學習持有這樣的觀點：知識是不能被傳遞的，而是基于主體經驗的主動建構，強調學習者的主動作用，強調學習的主動性。對于“商不變的性質”學生并不陌生，因為學生在進行整十數的口算除法時，已經有所接觸。本節課的關鍵是幫助學生完善對這一性質的認知。因此，在把握教學起點的情況下，首先通過問題情境激活已有經驗；接著讓學生自己說出商是2的除法算式，對這些除法算式進行整理、排序，引導學生觀察、思考這些除法算式的變化規律，指導學生進行描述；再引導學生抽象、概括出商不變的性質，最后通過分層練習幫助學生深化理解性質，至此，完成了幫助學生對商不變性質從模糊認識到清晰理解的認知完善過程。學生在這個過程中主動探索，知識逐步生長。這一過程也是數學規則學習從具體實例感知——語言抽象概括——具體實例運用的建構過程。

三、新知內化源于深刻的理解

抽象的數學規則必須在具體的實例中加以運用，這樣不僅能幫助學生理解數學規則，同時也發展了學生的數學應用意識。因此，在本課的鞏固練習環節中，練習作了精心設計，由易到難，由淺入深：練習1注重對性質中關鍵詞的理解，練習2引導學生發展擴大（或縮小）的倍數（0除外），練習3則運用性質進行簡化計算，而課堂小結中說一說生活中運用商不變的例子，讓學生體會數學與生活的聯系。最后，請手里卡片上算式得數與“28÷7=4”的得數相等的同學先出教室，既鞏固了知識，又檢查了效果，多種途徑幫助學生理解、內化新知。

與此同時也有幾點思考：一是學生回答“你還能說出幾道商是2的除法算式嗎？”這個問題時，說出的算式是被除數和除數同時擴大（或縮小）倍數不是整數倍的算式，該怎樣處理？是納入研究范圍還是放在一邊？二是由于學生現階段沒有學習0為什么不能做除數，對為什么不能同時乘（或除以）0缺乏理解認識，因此，這里的教學如何處理也是值得思考的問題。三是本節課我們教給學生的是什么？我們交給學生的不僅是商不變性質這個知識，更重要的是研究商不變性質的方法。學生通過觀察、比較除法算式后提出的猜想，實際是數學中的不完全歸納法，由于學生的知識水平有限沒有證明猜想，但是這種方法對于學生研究其他數學問題是很有幫助的，也許這就是“數學是思維的體操”的體現吧。

馮勝華中科技大學附屬小學邵承民武漢市硚口區武藥小學）

責任編輯 廖林