某車載導彈發射系統振動特性①

高星斗，畢世華，陳 陣

(北京理工大學 宇航學院，北京 100081)

0 引言

隨著未來高技術戰爭不斷發展的需要，對火箭導彈車載武器系統的機動性、反應能力、生存能力、發射精度和可靠性等提出了愈來愈高的要求［1］。為了保證車載導彈發射系統具有良好的動態性能和發射精度，首先必須準確計算出車載導彈發射系統的振動特性，建立起車載導彈發射系統的總體結構參數和布局與振動特性之間的定量關系，使車載導彈武器的固有振動頻率能得到合理分布，通過改變車載導彈發射系統的結構參數來改變車載導彈的振動頻率分布，以達到預定的設計要求。同時，獲取了車載導彈的特征值，即可進行車載導彈動力響應計算［2］。

車載導彈發射系統是彈性系統，工作時會產生振動。系統的振動有可能成為影響導彈發射可靠性和精度的重要因素或決定性條件［3］。因此，對車載導彈發射系統進行模態分析研究顯得非常重要。王彥平等用多重動態子結構法，分析了某型多管火箭炮的振動特性，計算了某工況下火箭炮的模態參數［4］。吳斌用動態縮聚法與雙協調子結構法相結合，計算了某型號導彈的振動特性［5］。唐靜靜等用多體系統傳遞矩陣法，計算了某自行火炮的振動特性［6］。

本文利用Pro/E軟件將建好的模型導入多體動力學分析軟件ADAMS中［7］，建立了車載導彈的多體系統發射動力學模型;分析計算了整體結構的振動模態;對比了結構計算結果及試驗結果，驗證了建模及分析方法的正確性。本文利用多體系統傳遞矩陣法［8］，解決了同時含有多個剛體和柔性聯接的車載導彈多體系統的固有振動特性這一計算難題，實現了對多聯裝車載導彈發射系統振動特性和動力響應的計算。

1 某車載導彈發射系統動力學模型

據某車載導彈發射系統的組成及動力學分析模型簡化要求，利用傳遞矩陣法并依據確定的傳遞方向，可將其由下至上依次劃分為車輪、車體(含底盤、發控艙以及附屬設備質量和轉動慣量的綜合)、回轉部分(不含起落部分)、起落部分(不含已擊發導彈和最新擊發導彈所在發射箱)，將最新擊發導彈所在發射箱尾部簡稱發射箱尾，并將它們視為各具6個自由度的剛體;最新擊發導彈所在發射箱視為空間運動彈性梁。每個部件可按自然屬性視為剛體、彈性梁和集中質量［9］。

車載導彈發射系統部件之間以各種鉸的形式連接，各種鉸根據其相關連接部件間的力學特性等效為由彈簧、扭簧、阻尼等力學元件構成。將大地視為無窮大靜止剛體，并編號為0，8個車輪和4個液壓支腿與地面的聯接，均用彈簧及與之并聯的阻尼器來等效，車體視作為空間運動的剛體;回轉部分(不含起落部分)視為空間運動剛體，編號為38;起落部分編號為40;起落架與第i個發射箱間的兩處聯接扭簧和彈簧及與之并聯的阻尼器分別編號為41+3i(i=1，2，3)、42+3i;第i個發射箱的后端面自由邊界編號為43+3i;第i個發射箱尾部編號為44+3i;第i個發射箱前支撐框與后支撐框之間的部分編號為45+3i，前支撐框前面的部分編號為46+3i;第i個發射箱的前端面自由邊界編號為47+3i。具體模型及體和鉸的編號見圖1。

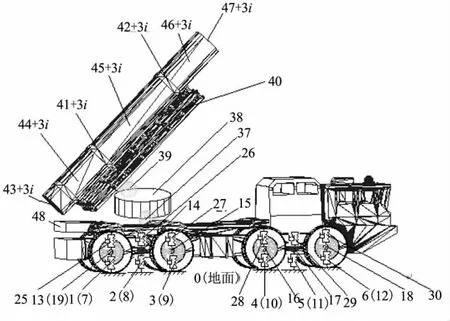
圖1 某車載導彈發射系統動力學仿真模型Fig.1 Simulation model of the vehicular missile launching system

2 車載導彈發射系統振動特性理論研究

計算復雜系統的振動特性時，可將它分割為若干個元素，各元素的特性可用矩陣來表示，把這些矩陣相乘，可反映整個系統特性的矩陣，利用兩端邊界條件，即可知道系統的振動特性［10］。

2.1 各點狀態矢量的定義

根據所建立的車載導彈系統發射動力學模型可知:該系統含有58個連結點，邊界點有18個(8個車輪和4個液壓支腿有12個接地邊界點，加上3個發射箱的前后端6個，合計18個)。因此，應定義76個狀態矢量。

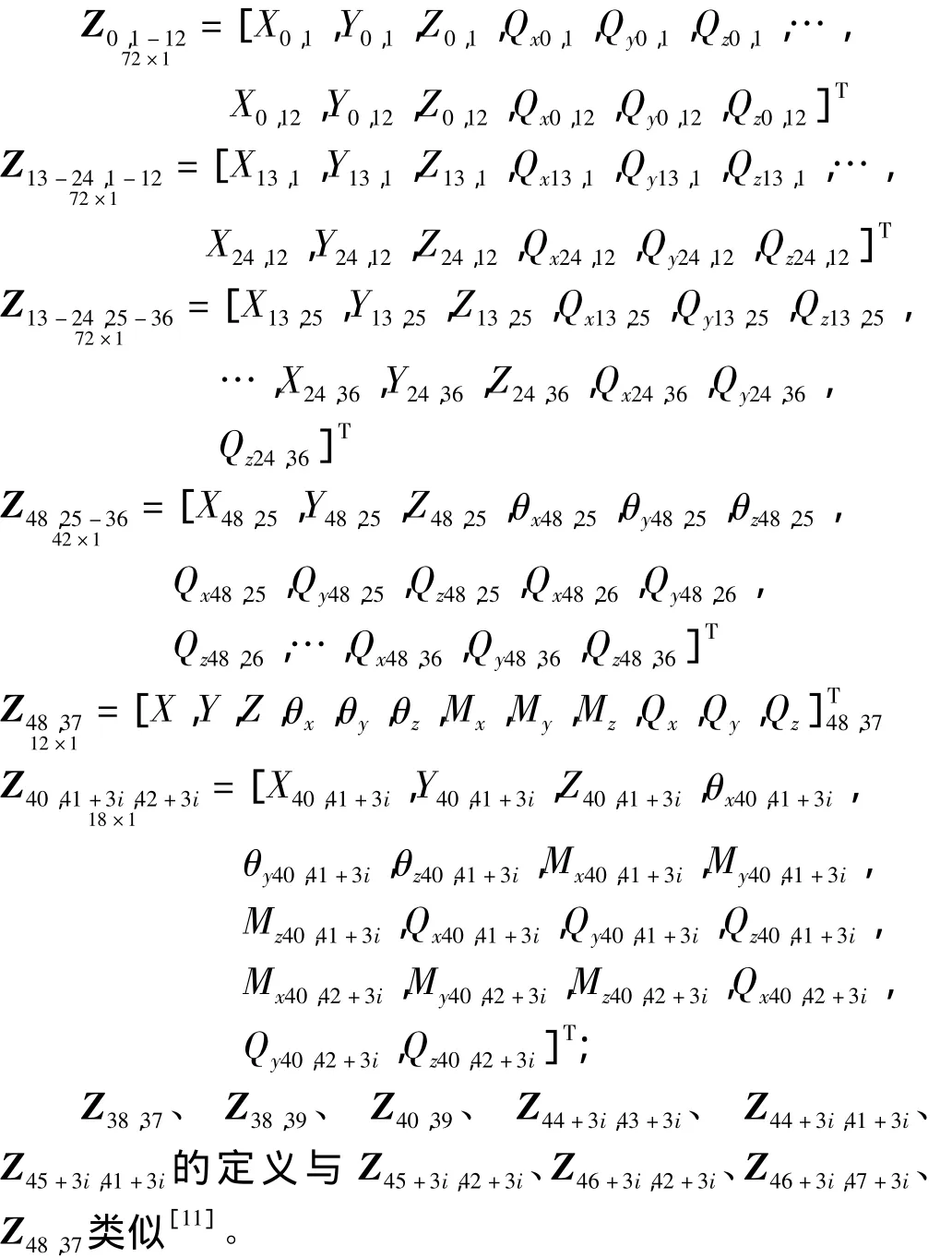
2.2 系統各元件的傳遞方程

式中 Ui表示體i或餃i的傳遞矩陣;Hα為方向射角所引起的變換矩陣;Hθ為高低射角所引起的變換矩陣［11］。

2.3 系統總傳遞方程

由以上各元件的傳遞方程可得車載導彈發射系統的總傳遞方程為

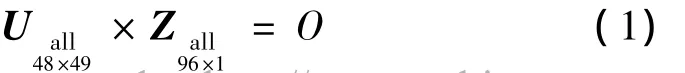
其中

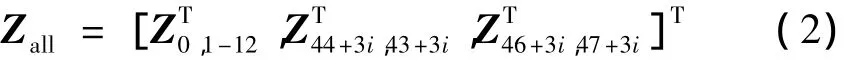
由系統邊界點的狀態矢量組成，車載導彈發射系統總傳遞矩陣為

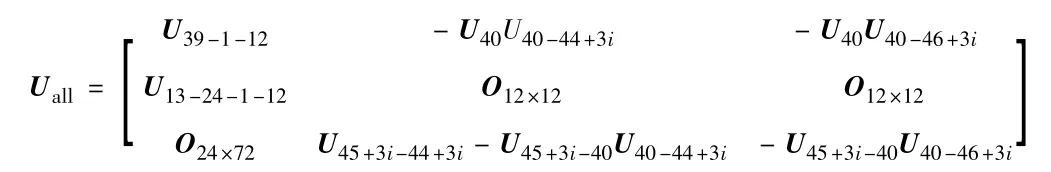
其中，Uall是48×96矩陣。

由式(2)可知，Zall是由系統的邊界點處的狀態矢量 Z0，1－12、Z44+3i，43+3i、Z46+3i，47+3i組成，對于邊界點處的狀態矢量，其一半元素由邊界條件確定;Z0，1－12中包含車載導彈發射系統8個車輪和4個液壓支腿與地面的12個接觸點在3個方向上的位移和力共72個元素，其中36個位移元素恒等于零，記去掉零元素的狀態矢量為發射箱尾點(44+3i，43+3i)和發射箱口點(46+3i，47+3i)的狀態矢量 Z44+3i，43+3i和 Z46+3i，47+3i中分別包含對應點的3個方向的線位移、角位移、力和力矩，每點12個元素中表示力和力矩的6個元素恒等于零，記去掉零元素的狀態矢量為和因此，去掉中的48個恒為零的元素，得到車載導彈發射系統的特征矢量為

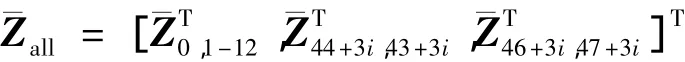
最后，可得車載導彈發射系統的特征方程為

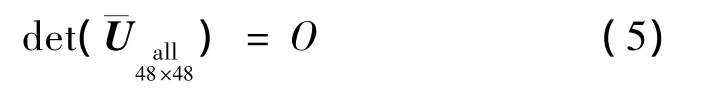
根據所建立的車載導彈發射系統的傳遞方程、傳遞矩陣和特征方程，最終可得到車載導彈發射系統的固有振動特性。

3 車載導彈振動模態試驗

為驗證所建發射動力學模型、所用參數和振動特性數值仿真的正確性，根據與相關單位合作進行的車載導彈的振動模態試驗結果，得到數值仿真計算結果與試驗結果吻合較好。試驗分為滿載、空載等4種工況，測量了其在滿載和空載等多種情況下的固有振動頻率、振型、阻尼比等模態參數。

4 車載導彈振動特性的計算實例

用本文方法和模型建立仿真系統，數值仿真了某車載導彈在方向角為0°，高低角為45°時的振動特性。在ADAMS中，對多體系系統進行模態分析一般要按兩步來執行計算:首先，計算全系統的靜平衡;然后，用所計算的靜平衡位置作為參考狀態位置，對系統進行模態分析。

由于導彈總質量接近發射系統發射箱和起落架的質量，使得導彈本身的質量對整個車載導彈發射系統振動特性的影響較大。因此，不計導彈對車載導彈發射系統振動特性影響的處理方法誤差較大。

表1給出了滿載裝彈情況下前10階固有頻率的計算結果及其與試驗結果的對比。對比表明，試驗結果與仿真結果的最大相對誤差絕對值小于10%，兩者吻合較好，驗證了所建動力學模型及本文理論的正確性。仿真計算結果前7階對應的振型如圖2所示。

從各階模態的振型來看，一階模態對應于起落部分繞耳軸轉動自由度;二階模態是發射車沿Z向平動與擺動自由度的耦合;三階模態對應著繞Y軸轉動自由度;四階模態是發射車沿X向平動與擺動自由度的耦合;五階模態對應著繞Z軸轉動自由度;六階模態對應著發射車車體繞X軸轉動自由度;七階模態是發射車車體上下垂直振動(沿Y軸移動)自由度。

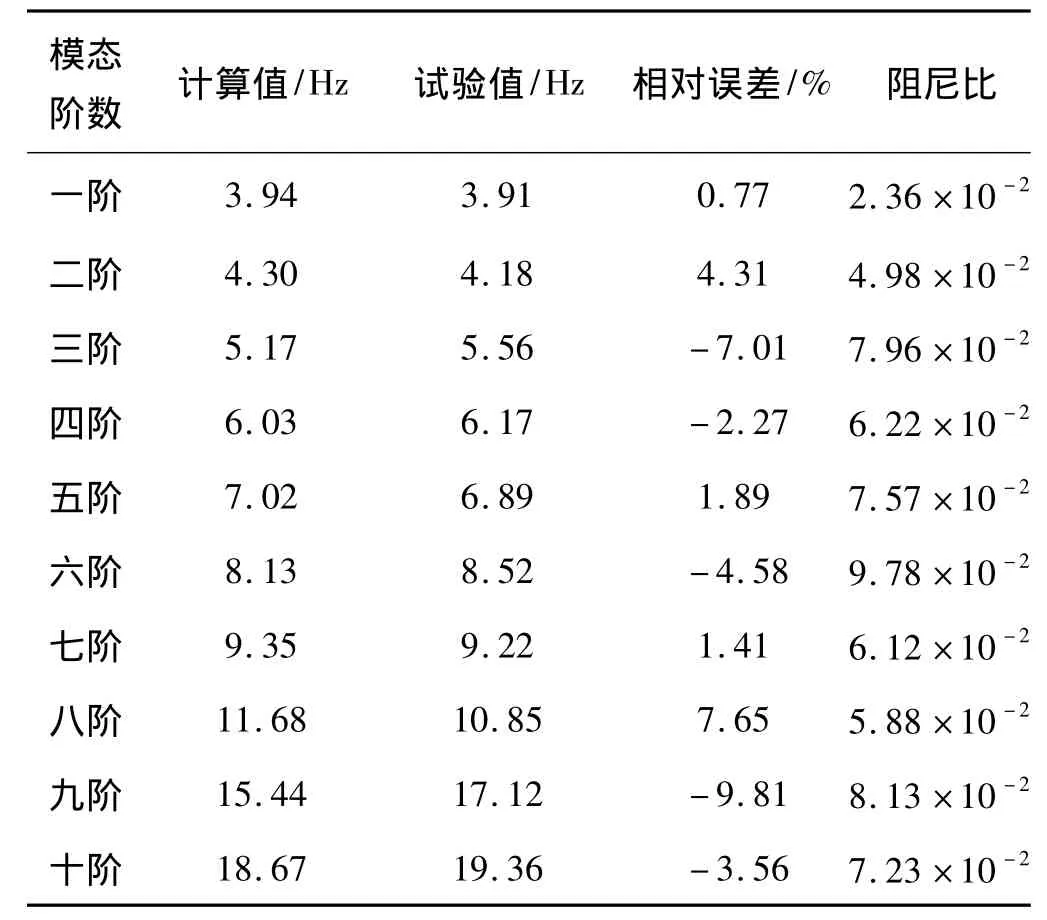
表1 滿載情況下頻率仿真結果與模態試驗結果對比Table 1 Frequency contrast between simulation and test results in the full load case

圖2 前7階的陣型圖Fig.2 Seven order vibration patters

5 結論

(1)應用多體系統傳遞矩陣法，得到了某車載導彈多體系統固有振動特性的理論解，解決了這一復雜計算難題。

(2)建立了某多聯裝車載導彈發射系統的發射動力學模型，分析計算得到了車載導彈發射系統整體結構的固有振動頻率和阻尼比，并得到了系統的前7階模態振型。從結果中可知滿載裝彈情況下發射系統的固有頻率在3～20 Hz范圍內。因此，在做設計時可避開系統的這個頻率范圍，而不致于使整個發射系統遭到共振破壞。

(3)通過與相關單位合作，進行車載導彈發射系統振動模態試驗，成功獲得了其振動特性，并與仿真計算結果進行了比較，驗證了該理論方法和仿真計算結果的正確性。

(4)用本文方法，某多聯裝車載導彈發射系統振動特性的仿真結果得到了試驗驗證，試驗結果與仿真結果的最大相對誤差絕對值小于10%，表明兩者吻合較好，驗證了所建動力學模型及本文理論的正確性。由此建立了多聯裝車載導彈發射系統整體結構的振動特性與總體布局結構參數的定量關系，從而可按預期目的通過修改多聯裝車載導彈的總體布局結構參數，達到改變振動特性，來提高多聯裝車載導彈發射系統的發射精度和動態性能。

［1］侯世明.導彈總體設計與試驗［M］.北京:宇航出版社，1996:9-13.

［2］芮筱亭，王國平.某遠程多管火箭振動特性研究［J］.振動與沖擊，2005(1):8-12.

［3］江金壽，程穎，馮慧華.車載火箭發射系統試驗模型模態研究［J］.強度與環境，2000(3):13-19.

［4］王彥平，申正賓.用動態子結構法分析火箭炮的振動特性［J］.中北大學學報，1989(2).

［5］吳斌.基于DRM的雙協調子結構法及其應用［J］.戰術導彈技術，1998(1):17-22.

［6］唐靜靜，芮筱亭，陸毓琪，等.自行火炮振動特性的計算［J］.彈道學報，2003(2):23-27.

［7］Timothy J McCoy.Wind turbine ADAMS model linearization including rotational and aerodynamic effects［J］.AIAA Journal，2004，1370:1-10.

［8］芮筱亭，黨雙喜，等.多體系統傳遞矩陣法在火炮動力學中的應用［J］.力學與實踐，1995，17(4):42-44.

［9］張太平，邵中年，周發明，等.某車載炮系統振動特性研究［J］.火炮發射與控制學報，2007(1):62-66.

［10］蔡德福.傳遞矩陣法在電機系統振動特性研究中的應用［J］.西北紡織工學院學報，1995，9(3):212-216.

［11］芮筱亭，陸毓琪，王國平，等.多管火箭發射動力學仿真與試驗測試方法［M］.北京:國防工業出版社，2003:25-56.