非凸區域上SPH計算結果后處理方法研究

鄭 俊，于開平，張嘉鐘，魏英杰

(哈爾濱工業大學航天學院，150001哈爾濱，zhengjun324203@126.com)

SPH(smoothed particle hydrodynamics)是一種基于Lagrangian描述的無網格方法［1］，其計算結果的后處理一般是直接將存儲于粒子上的數據與顏色矩陣關聯來獲得物質域上物理量分布［2］，無法得到基于網格的算法后處理的連續的等值線(面)圖、云圖、流線圖，且不易進行微積分運算以及切片上的數據可視化等.Massidda［3］指出無網格計算可視化是一項新的技術.Daniel［4］開發的面向SPH后處理的開源軟件Splash，需在Linux下編譯，主要面向天文領域，且該軟件包對于水動力學等其它領域的適用性還有待拓展.Biddiscombe等［5］基于Paraview開發了可處理SPH數據的程序，但其處理時還是直接在粒子上，并不方便，功能也不全面.無網格法計算可視化的理論［6-9］，主要是采用Delaunay三角化方法，將無網格點集進行三角化，獲得非結構化網格，然后基于非結構化網格進行后處理，可得到傳統計算可視化所得的各種圖形.但這些研究只針對于凸區域上的無網格點集，而非凸區域上的無網格計算可視化，鮮有報導.但在SPH所計算的液體飛濺、高速撞擊中的材料碎片等問題中，計算域都是非凸的，對非凸區域上的無網格點集進行Delaunay三角化將獲得一些并不屬于物質域的單元，稱這些單元為空白單元;如何方便的過濾掉這些單元，國內還沒有較系統的工作.文獻［6］采用在程序中事先指定邊界的方法來去除這些空白單元，但在SPH中，邊界處于復雜變化中，不可能通過事先指定.因此如何在復雜的非凸區域上進行Delaunay三角化并去除空白單元，從而為SPH算法提供后處理所需的網格，是非凸區域上SPH算法計算可視化急需解決的問題.

本文以凸區域上離散點集Delaunay三角化為基礎，提出一種“單元稱重”算法去除非凸區域上離散點集最小凸包三角化后形成的一些空白單元，準確得到了非凸區域SPH后處理所需要的網格，結合后處理軟件Tecplot實現了非凸區域上SPH計算結果的可視化.

SPH作為一種基于物質描述的無網格算法，在自由表面流動等領域得到了非常好的應用［2，10］，以至在流體的計算機實時動畫領域也開始采用該算法［11-12］，計算結果用很逼真的形象顯示出來.動畫領域對計算結果的處理，主要關注物質域表面的提取［10，13-14］及色澤處理，這些技術也是值得SPH算法后處理借鑒的.

1 SPH基本原理

SPH利用函數f與光滑函數w的加權積分來近似f與Dirac函數δ的卷積，從而可以近似得到f在計算域某點函數及空間導數的近似值［1］，離散后可得到

其中τj為粒子體積.利用它們，便可以將流體的動力學方程進行離散.由于本文側重的是計算可視化的探討，后文算例計算所需要的方程和參數會給出相應文獻出處，這里不再贅述.本文中所有算例的光滑函數為分段五次樣條函數［1］，初始光

2 物質域離散點集的Delaunay三角化及“單元稱重”法

對于任意一個離散點集，都存在一個最小凸包包含這些點.對該最小凸包進行Delaunay三角化，可形成由該離散點集的點作為節點的三角網格(單元)集，而且每1個三角單元的外接圓都不包含其它的節點;而由這些外接圓的圓心形成的多邊形稱為Voronoi圖［15］.離散點集的Delaunay三角化和Voronoi圖是計算幾何中最重要的算法，這里不再贅引.

2.1 凸區域離散點集上的Delaunay三角化

采用SPH粒子離散物質域之后，可以將SPH粒子集合的最小凸包進行Delaunay三角化，從而得到非結構化網格(或單元集)，并將SPH粒子作為單元節點，然后利用有限元插值方法，得到單元內任何一點處的物理量的值.對于凸區域上的離散點集(粒子集合)，也可借助Matlab中Delaunay算法來對其最小凸包進行三角化［7-8］.凸區域上離散點集的最小凸包的Delaunay三角化較為簡單，且是非凸區域上離散點集三角化的基礎.

2.2 非凸區域離散點集上的Delaunay三角化及“單元稱重”算法

對非凸區域點集直接進行Delaunay三角化會得到一些空白單元，這些單元包含任何物質.如圖1(a)所示，正方形區域的中心空洞中并沒有任何物質點，但是該點集最小凸包是包含所有粒子的正方形區域，因此該凸包也包含該正方形點集中心的空洞區域;當對該凸包進行三角化時，該空洞也同時被三角化了，如圖1(b)所示.

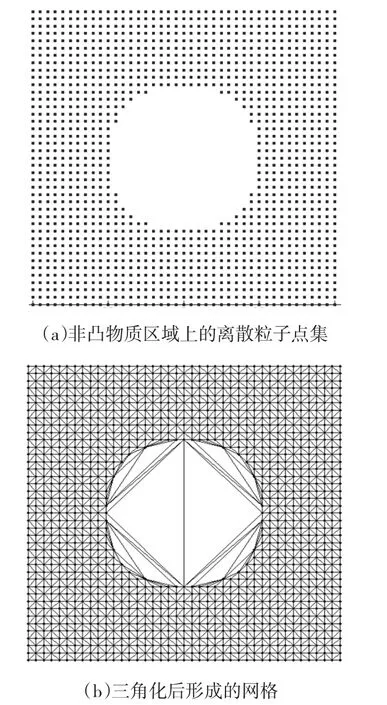
圖1 非凸區域的點集及其三角化后形成的空白單元

去除這些空白區域，文獻［6］通過事先指定邊界—比如指定空洞的周界，然后除掉處于該周界內的單元，剩下的單元就可以作為后處理的網格了.該方法對于靜變形，或材料(或計算域)不破碎、不卷曲的情況是可考慮應用的.但是在SPH領域，特別是波浪的飛濺、卷曲問題中，該方法無法應用.因此，本文提出一種“單元稱重”算法，可以去除各種復雜非凸區域上的離散點集三角化后形成的空白單元，并且其可行性在具有材料飛濺和粒子不均勻性的高速撞擊問題中得到了驗證.

2.2.1 空白單元過濾的“單元稱重”法

“單元稱重”法的基本思想是，不屬于物質域的空白單元，其質量比其它單元的質量或其節點(粒子)的質量要小很多，這類單元可以從單元集中去除.因此該算法的核心問題是，如何尋找1個方法來計算單元的質量，并提出1個比較的標準將它與周圍的粒子的質量進行比較，然后將其去除.解決這個問題，可以考慮將SPH求和近似算法式(1)結合三角單元的外心(也就是上文提到的相應三角網格的Voronoi多邊形的頂點)，具體算法如下.

每1個單元的位置用該單元的外心的位置re來表示，其中re為外心的矢徑，下標“e”表示單元的序號.而用外心處的加權質量來表征該單元的質量.因為該單元的外心正好是某Voronoi多變形的頂點，因此該單元的外接圓中將不含任何其它單元的其它節點，這確保了對該單元質量影響權重最大的是屬于該單元本身的節點;而該單元的所有節點到單元外心的距離都相等(都等于外徑)，確保了它的節點對其外心的影響權重相等.這些性質非常重要，這也是Delaunay三角化的優點.

要利用SPH求和近似得到外心處的加權質量，需要知道該單元外心處的光滑長度值.對任1個單元，可以取光滑長度為該單元所有節點的光滑長度的代數平均，即.其中j為該單元上節點的序號，h為光滑長度;利用式(1)可得單元加權質量me為

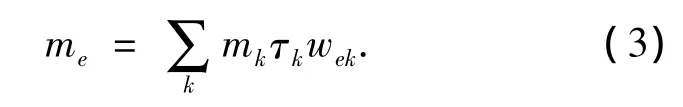
其中k為該單元外心的緊支域內支持粒子的序號.這些粒子可能不僅僅包含該單元本身上的節點，還可能包括周圍其它單元的節點;也有可能該外心的緊支域內不含任何支持粒子，甚至不含單元本身的節點—此時其加權質量為0.

通過下式—即“單元稱重”算法的定義式，來過濾掉不屬于物質域內的空白單元

因此式(4)可以表達為

式(4)可理解為，若計算所得單元的加權質量me小于該單元節點質量的平均值ˉm的一定量，那么該單元可以被過濾掉;式(6)可以理解為，若一個單元的加權質量因子βe小于事先設定的標準值βs，則這個單元應該被過濾掉.對于圖1(b)中非凸區域的離散點集三角化后形成的空白單元，利用“單元稱重”法就可以去除，如圖2所示.

由圖2可發現，當βs不同時，可以過濾掉一部分共同的空白單元.βs較小時，過濾后周界顯得光滑，如圖2(a);βs變大時，周界顯得較不光滑，如圖2(c).這是因為βs較小時，只有那些加權質量me特別小的單元被過濾掉，被過濾掉的單元較少，所以邊界處顯得光滑;而βs變大時，有些加權質量不是特別小的單元也被過濾掉;βs越大，被過濾掉的單元越多.注意到，式(3)中粒子對單元外心的權重wek與單元的外徑成反比關系，所以外徑越大的單元(也就是單元空間尺寸越大)，其加權質量自然越小.

特別是當臨界加權質量因子βs=0時，只有那些加權質量為0的單元被過濾掉，此時表現為因為單元外徑太大，該單元上的3個節點都對單元的外心的權重wek為0.考慮到SPH中粒子間存在相互作用的概念是基于wek不為0，所以可以將這些節點對其單元的加權求和稱為對外心的作用.注意到SPH中粒子間的互相作用在數學上表現為wek不為0，但在物理意義上表現為粒子間的作用力不為0.而在連續介質力學中，力的產生是因為相鄰的物質發生相對運動或變形，即力就是物質的相互作用.因此如果兩點之間不互相作用，那么可以認為這兩個點上的質量粒子沒有相互接觸.所以如果三角單元上的節點對其外心沒有作用，即wek為0，那么可認為該單元上的粒子與其外心間沒有質量接觸;而沒有質量接觸，則表明該單元內部有質量間斷，該單元就自然可被過濾掉.可見單元稱重算法是一種符合物理意義的算法.而βs＞0的含義是把單元內粒子間互相作用極其微弱的單元也過濾掉.

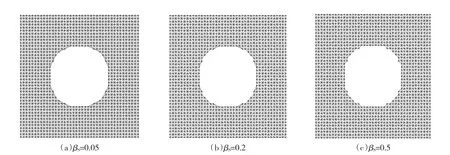
圖2 βs不同時，“單元稱重”法去除空白單元的情況

下面對單元稱重法為什么能過濾掉空白單元進行更深層次考察.主要出發點是考察空白單元的尺寸和加權質量因子βe間的關系.

2.2.2 “單元稱重”法過濾空白單元的可行性分析

首先給出單元稱重算法可行的直觀解釋.由圖1可以發現空白單元的3個節點中只要有一對節點的連線跨越了空白區域，則這個連線的距離就會比較大.而該空白單元的3個節點中，只要有2個節點之間的連線距離比較大，那么外接圓半徑就會很大，而外徑很大時，根據光滑函數的衰減特性可知，這3個節點對該單元外心處的權重wek就會迅速減小并接近于0.而圖2(a)中處于邊界附近的小單元依然可以保存下來，原因也正在于此，即它們之間的連線并未完全跨越空白區域.

定義單元的特征長度為外接圓半徑，并定義單元的特征尺度為特征長度與其光滑長度之比，記為γe.顯然，只要某單元的特征長度接近于光滑函數wek的緊支域半徑，那么單元的加權質量就為0，那些特別大的空白單元就立即被過濾掉;而那些單元特征長度大于光滑長度而接近于緊支域半徑的，因為光滑函數的衰減性質，由式(3)所得的加權質量會非常小，于是由式(4)中βs的大小決定它們是否被過濾掉.

為了給出式(4)的定性分析，在一個等邊三角形的單元上，根據式(3)和(4)，繪制出該單元本身加權質量因子βe隨單元特征尺度變化的大致關系，如圖3所示.由圖3可知，隨γe增長，曲線、橫坐標線及γe豎線圍成的曲邊三角區域越來越小.特別是當尺度因子γe接近2.5時，也就是單元尺度接近于2.5倍的光滑長度時，此時βs≈0，即只有那些加權質量me接近于0的單元被過濾掉，剩下的大多數單元被保存下來.隨著尺度因子γe的縮小，并接近1.5時，被過濾的單元數量幾乎不變，如圖中的最大曲邊三角形，此時βs≈1，也就是那些單元加權質量me小于粒子平均質量ˉm的單元基本上都被過濾了(即那些粒子對其外心作用比較弱的甚至稍強的也都被過略掉了)，保留下的單元其質量都大于其節點的平均質量.這可作為圖2中隨著臨界βs增大，被過濾的單元幾乎不變的原因，因為剩下的可被過濾的單元越來越少.

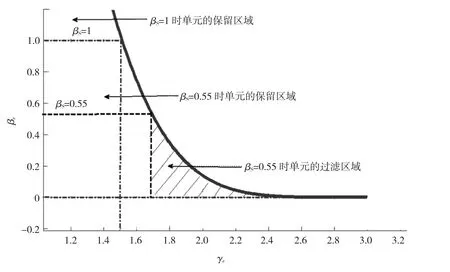
圖3 單元加權質量隨其特征尺度的變化關系

“單元稱重”法中反映一個單元是否可被過濾的參數，即加權質量因子βe，它反映了一個單元內部所含質量的多少，是單元內部粒子之間作用強弱的表現.從以上分析中還可得知，它也是單元尺度γe小或大的間接體現.也就是說，本質上講，式(6)是根據被過濾單元尺度γe來判定哪些大尺度的單元是可以被過濾掉的—這與SPH中粒子間是否是粒子作用對是由它們之間距離來判斷的思想是一致的.

臨界加權質量因子βe的合理范圍，可以根據圖3中的曲線來估計.一般地，如果尺度因子為2以上，即特征長度為2倍光滑長度以上的單元被過濾掉，那么根據圖3，就可以得到此時βs≈0.15.

3 SPH后處理的有限元插值方法及數值算例

形成網格后，就可由網格節點上所存儲的物理量的數值進行有限元插值，從而得到網格單元內各點處的相應數值.完成這個過程，可選擇自主開發程序，也可利用現有軟件，如Tecplot［16］.而要利用成熟的后處理軟件Tecplot精確處理SPH這些數據，就需要將SPH數據轉換到離散該物質域的有限元格式，從而實現有限元插值.圖4為液滴問題［17］的幾個時刻的處理結果.三維時的情是類似的.

非凸區域上的SPH算法后處理同樣如此，但是需要將離散點集三角化之后，利用“單元稱重”法將空白單元過濾掉，再將SPH數據結合過濾后的單元集用有限元格式導入到Tecplot中處理.若圖2區域上各粒子上具有F=sin(x2+y2)cos(x2-y2)的物理量，則其利用以上SPH算法的后處理方法得到的曲面與等值線云圖如圖5所示.Tecplot功能遠不限于此;它還具有微積分、切片、光照等功能.

對于大多數基于SPH的研究，本文方法已足夠使用.特別是去除非凸區域上離散點集三角化的空白單元，“單元稱重”法簡潔且適應性強.值得注意的是，“單元稱重”法不需要事先判斷該點集是否屬于非凸區域，而是直接進行單元過濾.因此只要程序中加入該算法，不但不對凸區域上點集三角化后形成的的單元有影響，而且可直接對非凸集三角化后的單元進行過濾.

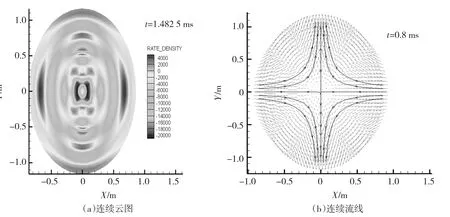
圖4 凸區域上利用有限元插值方法得到的SPH后處理結果

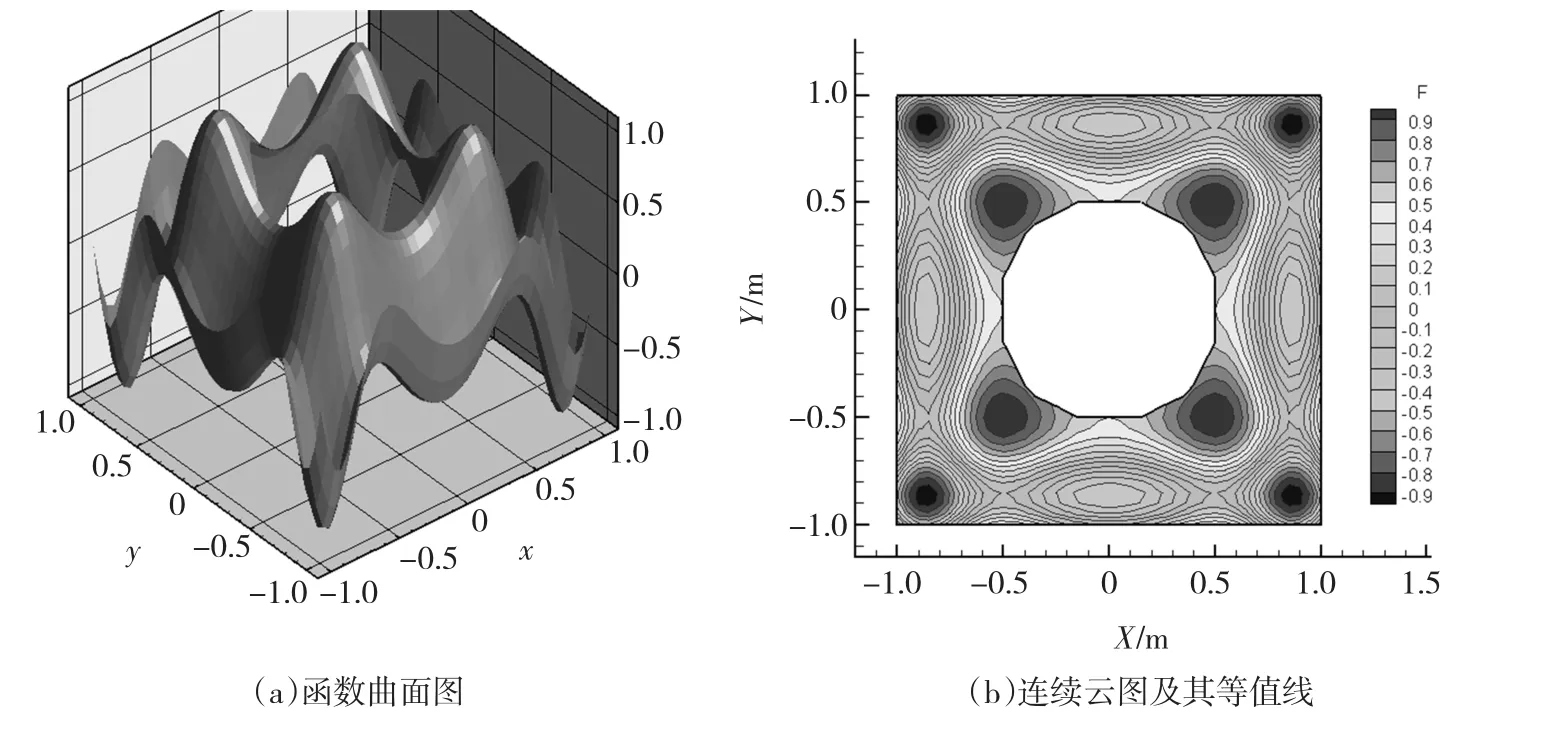
圖5 非凸區域上利用有限元插值方法得到的SPH后處理結果

3.1 “單元稱重”算法在粒子非均勻分布與材料飛濺情況的適應性

以上所計算的算例粒子分布都比較均勻，如圖4～5.為了檢驗“單元稱重”法對實際復雜情況的適用性，本文計算了一個高速撞擊問題，在該算例中具有較嚴重的粒子分布不均勻性與材料飛濺問題.控制方程同文獻［17］，計算域如圖6(a)～(c)所示，粒子的間距為5.0×10-2m，而時間步長為5.0 μs，取人工粘性常數αII=1，βII=2［17］.球形液滴以1 000 m/s初始速度向左運動.2.5 ms和12.5 ms時粒子分布、三角化后的單元集以及經過加權質量因子βs=1.0e-3過濾后的單元集，如圖6所示.

圖6 不同時刻粒子分布及在其最小凸包上三角化形成的單元集和過濾后的情形，βs=1.0e－3

4 結論

本文提出一種“單元稱重”算法，用于去除非凸區域上離散點(粒子)集的三角化后形成的空白單元.“單元稱重”法只過濾非凸區域離散點集的三角化后形成的空白單元，而對凸區域上離散點集三角化形成的單元沒有影響，該方法簡潔且對復雜的非凸區域適應性較強.利用“單元稱重”法過濾后的單元集，結合SPH計算所得數據，并將數據文件寫成有限元格式，導入到Tecplot中進行直接后處理，獲得傳統科學計算可視化所需的計算圖形，為SPH算法的后處理，提供了一種實用簡潔的途徑.該方法的適用性和可行性在具有材料飛濺和粒子不均性的數值算例中得到了驗證.

［1］LIU G R，LIU M B.光滑粒子流體動力學—一種無網格粒子法［M］.韓旭，楊剛，強洪夫，譯.長沙:湖南大學出版社，2005:1-200.

［2］OGER G，DORING M，ALESSANDRINI B，et al.Twodimensional SPH simulations of wedge water entries［J］.Journal of Computational Physics，2006，213(2): 803-822.

［3］MASSIDDA L.ARMANDO，a SPH code for CERN-some theory，a short tutorial，the code description and some examples［R］.［S.l.］:European Organization for Nuclear Research，2008.

［4］DANIEL P.Visualisation of SPH data using SPLASH-v1.9.1［EB/OL］.2007-9-12.http://www.astro. ex.ac.uk/people/dprice/splash/index.html.

［5］BIDDISCOMBE J，GRAHAM D，MARUZEWSKI P.Interactive visualization and exploration ofSPH data［C］//Second International Workshop of Smoothed Particle Hydrodynamics European Research Interest Community.Madrid:［s.n.］，2007.

［6］文建波，周進雄，張紅艷，等.基于Delaunay三角化的無網格法計算結果后處理［J］.應用力學學報，2003，4(20):600-601.

［7］田仲可.基于面片句柄對象的無網格法可視化研究［J］.計算機工程與設計，2008，29(13):3513-3515.

［8］史寶軍，袁明武，陳永強.無網格方法數值結果的可視化方法與實現［J］.工程力學，2004，21(6):51-55.

［9］ZHOU J X，WEN J B，ZHANG H Y，et al.A nodal integration and post-processing technique based on Voronoi diagram for Galerkin meshless methods［J］.Comput Methods Appl Mech Engrg，2003，192:3831-3843.

［10］BECKER M，TESCHNER M.Weakly compressible SPH for free surface flows［C］//Eurographics ACM SIGGRAPH Symposium on Computer Animation.San Diego:［s.n.］，2007:63-72.

［11］柳有權，劉學慧，朱紅斌，等.基于物理的流體模擬動畫綜述［J］.計算機輔助設計與圖形學學報，2005，17(12):2581-2589.

［12］KOUMOUTSAKOS P，COTTET G H，ROSSINELLI D. Flow simulations using particales bridging computer graphics and CFD［R］.http://www.cse-lab.ethz.ch/ teaching/classes/mulsup.html.

［13］ROSENTHAL P，ROSSWOG S，LINSEN L.Direct surface extraction from smoothed particle hydrodynamics simulation data［C］//Proceedings of the.4th High-End VisualizationWorkshop. Berlin:LehmannsMedia，2007:50-61.

［14］KIM J，CHA D，CHANG B，et al.Practical animation of turbulent splashing water［C］//In Proceedings of the 2006 ACM SIGGRAPH/Eurographics Symposium on Computer Animation.Eurographics:［s.n.］，2006: 335-344.

［15］周培德.計算幾何—算法分析與設計［M］.北京:清華大學出版社，2000:1-100.

［16］TECPLOT.Tecplot 10 Release 6 on line help［EB/ OL］.www.tecplot.Com/support.

［17］FANG J，PARRIAUX A，RENTSCHLER M，et al. Improved SPH methods for simulating free surface flows of viscous fluids［J］.Applied Numerical Mathematics，2009，59(2):251-271.