自適應反演滑模控制在火箭炮交流伺服系統中的應用

郭亞軍，王曉鋒，馬大為，樂貴高

( 南京理工大學 機械工程學院，江蘇 南京210094)

防空多管火箭炮在不同的帶彈量下，其轉動慣量及不平衡力矩大范圍變化，且發射時負載阻力矩、不同彈種共架發射的負載變化等，使得系統存在嚴重的非線性。傳統的火箭炮位置控制采用線性PI或PID 控制［1］，沒有考慮模型中的非線性特性和參數不確定性，難以保證控制品質及適應大負載、大轉動慣量及強干擾的場合。滑模變結構控制對于模型參數的不確定性具有強魯棒性，但是存在“抖振”問題［2-4］。反演控制是一種針對控制對象的變化和環境干擾影響而提出的控制策略［5］，它采用反復選擇合適的狀態空間函數作為控制輸入，通過迭代、反推和Lyapunov 函數的優化，進而完成整個控制器的設計。Zhou［6］、胡建輝［7］及王家軍等［8］設計了自適應反演速度控制器，對伺服系統的速度環進行了仿真分析，但未進行位置控制的研究。

為了使系統具有更好的控制特性，劉正華等［9］提出了自適應反演滑模的方法，并應用于三軸虛擬仿真臺，實現了系統較強的魯棒性。高劍［10］等將這種方法應用于水下航行器。

基于自適應反演滑模控制方法，研究了火箭炮俯仰運動的位置控制問題，獲得了良好的全局穩定性和跟蹤特性，降低了對外界擾動的敏感性。

1 問題描述

多管火箭炮位置伺服系統的執行元件由永磁同步伺服電動機( PMSM)構成，系統速度環和位置環控制采用數字控制，其電氣原理圖如圖1所示。其工作原理是:全炮控制臺根據火炮位置給定值與當前實際的位置，計算出誤差，并以該誤差作為自適應反演滑模控制算法的輸入，由該算法得出實際控制量，最終通過D/A 轉換器傳送到伺服放大器中，由電路放大后，通過俯仰和方位驅動器控制交流伺服電動機，從而經過減速器及回轉機構改變火箭炮的方位與仰角。

圖1 火箭炮位置伺服系統結構原理圖Fig.1 Sketch of position servo system structure of rocket gun

2 基于電流解耦控制的永磁同步電動機線性化數學模型

假設:

1)忽略飽和效應;

2)電動機氣隙磁場均勻分布，感應反電動勢呈正弦波狀;

3)磁滯及渦流損耗不計;

4)勵磁電流無動態響應;

5)轉子上無勵磁繞組;

6)采用轉子磁極位置定向的矢量控制時的定子電流勵磁分量Id=0.

根據以上假設，可寫出轉子坐標系即dq 坐標系下系統的線性化數學模型

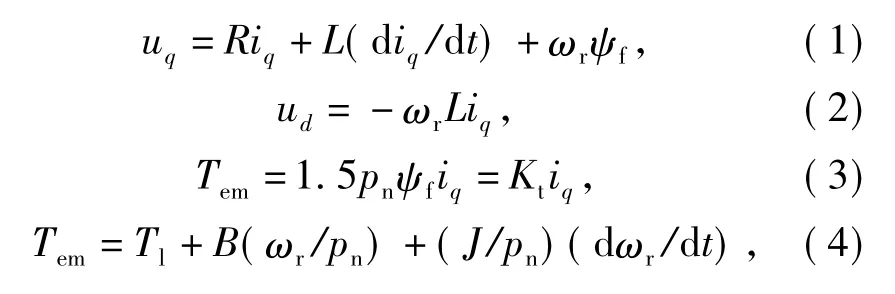
式中:ud，uq為dq 坐標系上的電樞電壓分量; iq，id為dq 坐標系上的電樞電流分量;L 為dq 坐標系上的等效電樞電感( L=Ld=Lq); R 為電樞繞組電阻; ωr為dq 坐標系的電角速度; Ψf，pn為永久磁鐵對應的轉子磁鏈和電機極對數;Kt為電磁轉矩系數; Tem，Tl分別為電磁轉矩和負載力矩; B，J 分別為阻尼系數和轉動慣量。

在PMSM 位置伺服三閉環控制系統中，由于電流環采用滯環控制方式，因此可以把包括電流環在內的PMSM、逆變器看成廣義的“被控對象”。因逆變器包括電流環內，而考慮到電磁時間常數比機械時間常數小得多，且電流環速度遠快于速度環和位置環的響應速度，故可將電流環近似簡化為比例系數為1 的比例環節［1］，自適應反演滑模控制器是將位置調節器與速度調節器合二為一。

結合目前設備中采用的減速器及回轉機構是高精度器件，忽略其間隙等因素對系統的影響，所以以上討論的俯仰系統采用半閉環控制方式是可行的。

令x1=θr，x2=ωr=，可建立火箭炮位置伺服系統的狀態空間方程

將(5)式改寫為

式中:Am=-B/J; Bm=p2nΨf/J，F( t)=(-pn/J)Tl.

3 自適應反演滑模控制器原理

3.1 反演滑模控制器設計

步驟1 首先定義位置跟蹤誤差e1，位置指令為θref，取虛擬控制量α1=c1e1，其中c1為正常數，則

定義Lyapunov 函數

定義

由(9)式和(10)式可以得到

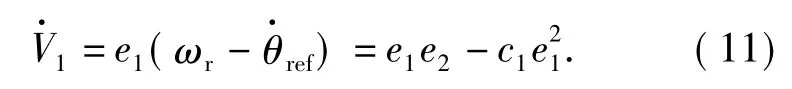
步驟2 對(10)式求導可得

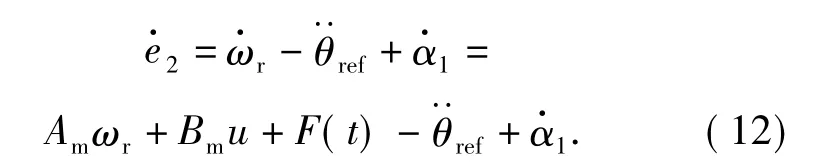
定義Lyapunov 函數

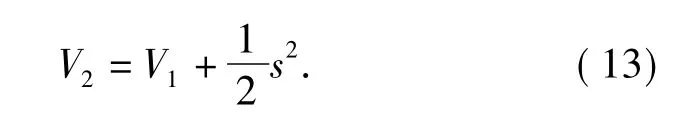
定義切換函數

式中k1＞0.

對(13)式求導得

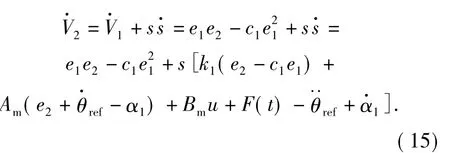
3.2 不確定上界的確定

一般控制對象的不確定因素的上界值很難預知，為了避免采用F 的上界問題，采用自適應算法預估F 值。

定義Lyapunov 函數

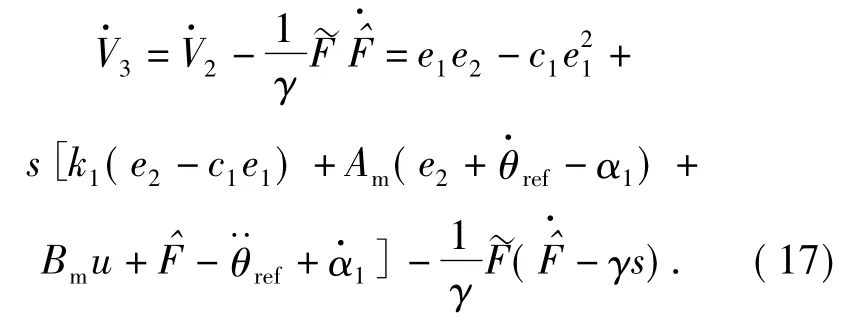
所以可設計自適應反演滑模控制器為

式中:h，β 為正常數。

自適應率為

3.3 穩定性分析

通過分析Lyapunov 函數得到系統穩定性的條件，將(18)式和(19)式代入(17)式可得

故(20)式可寫為

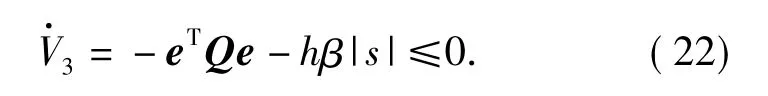
由Lyapunov 穩定性可知

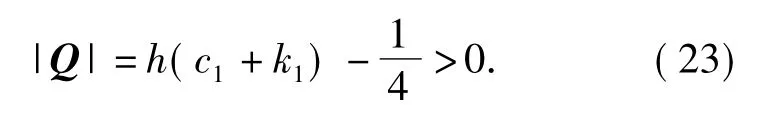
通過取h，c1和k1的值來保證Q 為正定矩陣，即≤0.

4 仿真研究

根據以上數學模型分別設計PID 控制器和自適應反演滑模控制器。仿真系統圖如圖2所示，系統主要參數:系統電機及負載轉動慣量經折算后為J=8.627 ×10-3kg·m2;系統不平衡力矩和摩擦力矩經折算后為4.86 N·m;系統外部燃氣流沖擊干擾力矩及未建模動態折算后為10 N·m，電磁轉矩系數Kt=1.11 N·m/A; 阻尼系數B=1.43 ×10-4N·m·s; 定子電阻Ra=2.6 Ω; 繞組電感Ld=Lq=50 ×10-3H;額定電流Ie=6.4 A;容許最大電流Imax=12.8 A;磁極對數Pn=4.反演滑模控制器參數取: c1=150，k1=150，h=500，β=20，γ=18.PID 控制器位置環參數取kp1=10，kI1=0.01，kD1=0.3，速度環參數取kp2=8，kI2=22.5，kD2=0.8.

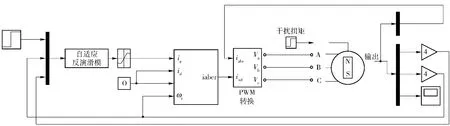
圖2 火箭炮交流位置伺服系統仿真結構圖Fig.2 Simulation block diagram of AC position servo system

利用MATLAB 軟件進行計算機仿真，結果如圖3～圖6所示，圖3在0.5 s 負載突加15 N·m 的干擾力矩，圖4為系統轉動慣量變化2 倍時的響應曲線，圖5為自適應反演滑模控制時的空載跟蹤誤差曲線，圖6為PID 控制時的空載跟蹤誤差曲線。俯仰正弦跟蹤等效正弦輸入信號為5sin(0.713 6t).

圖3 施加負載擾動時的階躍響應曲線Fig.3 Step response subjected to load disturbance

圖4 轉動慣量變化2 倍時的階躍響應曲線Fig.4 Step response in double moment of inertia

圖5 自適應反演滑模控制的誤差曲線Fig.5 Error of adaptive backstepping slide mode control

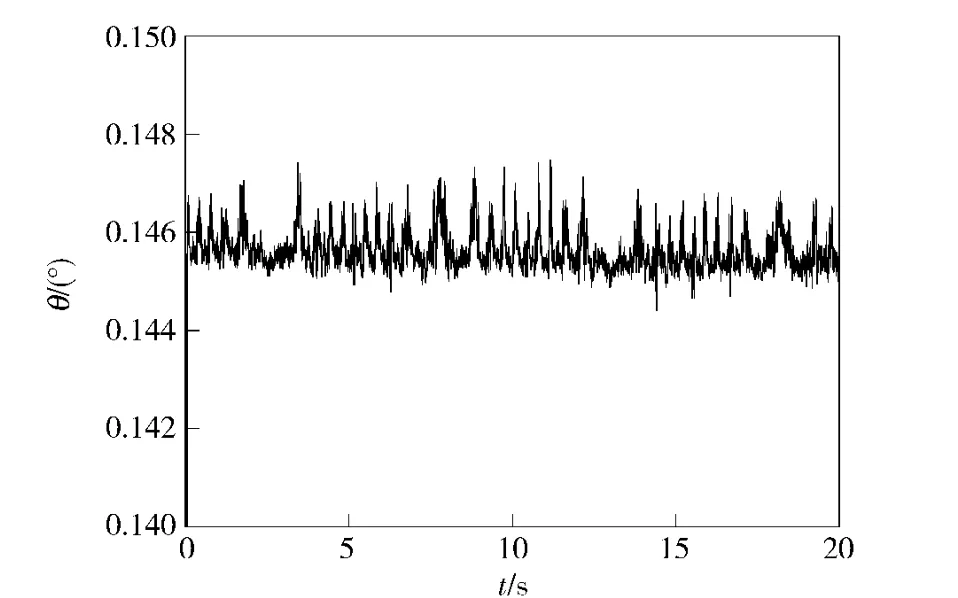
圖6 PID 控制的誤差曲線Fig.6 Error of PID control

由圖3、圖4及圖6可以看出，經典控制對系統擾動抵抗能力較差，穩定時出現了靜態誤差，同時對系統慣量的變化較為敏感，響應變慢，產生較小的超調，跟蹤誤差較大。由圖3～圖5可以看出，自適應反演滑模控制對系統負載擾動不敏感，具有較強的魯棒性，對參數的攝動無振蕩無超調，跟蹤誤差相對于PID 控制較小，具有明顯的優勢。

5 結論

將自適應反演滑模控制應用于火箭炮位置伺服系統俯仰控制，建立了基于MATLAB/Simulink 的數學模型。仿真結果表明，此控制算法有效的消除了系統靜差，對系統參數的攝動及負載干擾具有較強的魯棒性，并且獲得了較好的跟蹤效果，穩定性的理論分析及仿真研究都證明了該控制器的有效性。

References)

［1］ 朱玉川，馬大為，李志剛，等.帶積分項火箭炮最優滑模伺服控制［J］.兵工學報，2007，28(10):1272-1275.ZHU Yu-chuan，MA Da-wei，LI Zhi-gang，et al.Optimal sliding mode servo control with integral term for rocket launcher［J］.Acta Armamentarii，2007，28(10):1272-1275.( in Chinese)

［2］ 柴華偉，馬大為，李志剛，等.交流伺服系統最優內模滑模控制器設計與應用［J］.南京航空航天大學學報，2007，39(4):510-513.CHAI Hua-wei，MA Da-wei，LI Zhi-gang，et al.Design and application of optimal MC-SMC in AC Servo systems［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2007，39( 4):510-513.( in Chinese)

［3］ 閆茂德，張長青，賀昱曜.一類不確定非線性系統的狀態參考自適應滑模控制［J］.西北工業大學學報，2004，22(4):448-451.YAN Mao-de，ZHANG Chang-qing，HE Yu-yao.State reference adaptive sliding mode control for a class of nonlinear systems with uncertainties［J］.2004，22(4):448-451.( in Chinese)

［4］ 張春喜，孫立軍，朱建良，等.永磁電機的控制技術［J］.電機與控制學報，2005，9(1):15-19.ZHANG Chun-xi，SUN Li-jun，ZHU Jian-liang，et al.Control technology of permanent magnet motor［J］.Electric Machines and Control，2005，9(1):15-19.( in Chinese)

［5］ 張鵬，李穎暉，肖蕾.基于遞歸神經網絡的伺服系統自適應反步控制［J］.系統仿真學報，2008，20(6):1475-1478.ZHANG Peng，LI Ying-hui，XIAO Lei.Adaptive-backstepping control for servo system based on recurrent-neural network［J］.Journal of System Simulation，2008，20(6):1475-1478.( in Chinese)

［6］ Zhou J，Wang Y.Adaptive backstepping speed controller design for a permanent magnet synchronous motor［J］.IEE Proc-Electric Power Application，2002，149(2):165-172.

［7］ 胡建輝，鄒繼斌.永磁同步電動機自適應反步控制的建模與仿真［J］.系統仿真學報，2007，19(2):247-303.HU Jian-hui，ZOU Ji-bin.Modeling and simulation for adaptive backstepping control of PMSM［J］.Journal of System Simulation，2007，19(2):247-303.( in Chinese)

［8］ 王家軍，趙光宙，齊冬蓮.反推式控制在永磁同步電動機速度跟蹤控制中的應用［J］.中國電機工程學報，2004，24( 8):95-98.WANG Jia-jun，ZHAO Guang-zhou，QI Dong-lian.Speed tracking control of permanent magnet synchronous motor with backstepping［J］.Proceedings of the CSEE，2004，24( 8):95-98.( in Chinese)

［9］ 劉正華，吳云潔，爾聯潔，等.自適應反演滑模轉臺魯棒控制器設計［J］.系統仿真學報，2006，18(2):894-896.LIU Zheng-hua，WU Yu-jie，ER Lian-jie，et al.Design of robust controller based on adaptive backstepping and slide mode for flight motion simulator［J］.Journal of System Simulation，2006，18(2):894-896.( in Chinese)

［10］ 高劍，徐德民，李俊，等.自主水下航行器軸向運動的自適應反演滑模控制［J］.西北工業大學學報，2007，25( 4):552-554.GAO Jian，XU De-min，LI Jun，et al.Adaptive backstepping sliding mode control for surge motion of an autonomous underwater vehicle［J］.Journal of Northwestern Polytechnical University，2007，25(4):552-554.( in Chinese)