LCL濾波并網逆變電源的控制策略研究

鄧翔， 胡雪峰，2， 龔春英

(1.南京航空航天大學自動化學院，江蘇南京 210016;

2.安徽工業大學電力電子與運動控制省重點實驗室，安徽馬鞍山 243002)

LCL濾波并網逆變電源的控制策略研究

鄧翔1， 胡雪峰1，2， 龔春英1

(1.南京航空航天大學自動化學院，江蘇南京 210016;

2.安徽工業大學電力電子與運動控制省重點實驗室，安徽馬鞍山 243002)

針對LCL濾波的并網逆變電源采用直接并網電流單閉環控制時，存在系統穩定性和控制精確度等問題，提出一種控制策略。控制方案采用電網側直接入網電流有效值作為外環反饋值，橋臂側電感電流的瞬時值作為內環反饋值的雙閉環控制策略，對該方案進行系統建模并結合勞思－赫爾維茨穩定判據驗證控制系統的穩定性，給出該控制策略的理論依據和實現方法。在一臺以DSP為核心控制器件的1kVA光伏電池并網逆變電源裝置上進行實驗驗證。實驗結果表明，該控制策略既保證了系統的穩定性，又提高了入網電流的直接控制精確度，能同時實現并網逆變電源的高精確度并網電流穩態輸出波形和快速動態響應性能。

并網逆變器;LCL濾波器;控制策略;系統建模;穩定性

0 引言

可再生能源并網發電系統中，由于LCL型濾波器對高頻諧波電流可起到很大的衰減作用，更有利于并網逆變器在較低開關頻率下獲得高質量的饋網電流，因此LCL型濾波器在并網逆變電源中得到了廣泛應用［1－3］。但是，LCL型濾波器是一個三階系統，容易造成系統振蕩，對系統的控制策略提出了更高要求。文獻［4－5］己經從系統穩定性進行分析得出基于并網電流單環控制方法無法使系統穩定運行，采用橋臂電流控制方法，來間接實現對并網電流的控制時，不僅滿足并網電流的功率因數要求，而且閉環系統是穩定性的，但這種方法沒有涉及到直接饋網電流變量，所以很難做到饋網電流的精確控制，本文在此基礎上提出一種雙閉環控制策略，采用直接饋網電流的幅值有效值控制作為外環，把外環輸出與鎖相后的單位電網電壓相乘后的積作為內環給定，把橋臂輸出電流的瞬時值作為內環的反饋量并對系統進行建模和穩定性分析，期望實現對饋網電流的直接控制，又保證饋網電流具有較低的諧波含量和很高的功率因數。

1 系統模型分析

采用LCL型濾波器的單相并網逆變電源系統的原理如圖1所示。如果忽略直流母線電壓的波動且把開關元件視為理想器件，當開關頻率遠遠大于50Hz時，可以把圖1中的非線性逆變橋系統視為線性系統［6－11］。

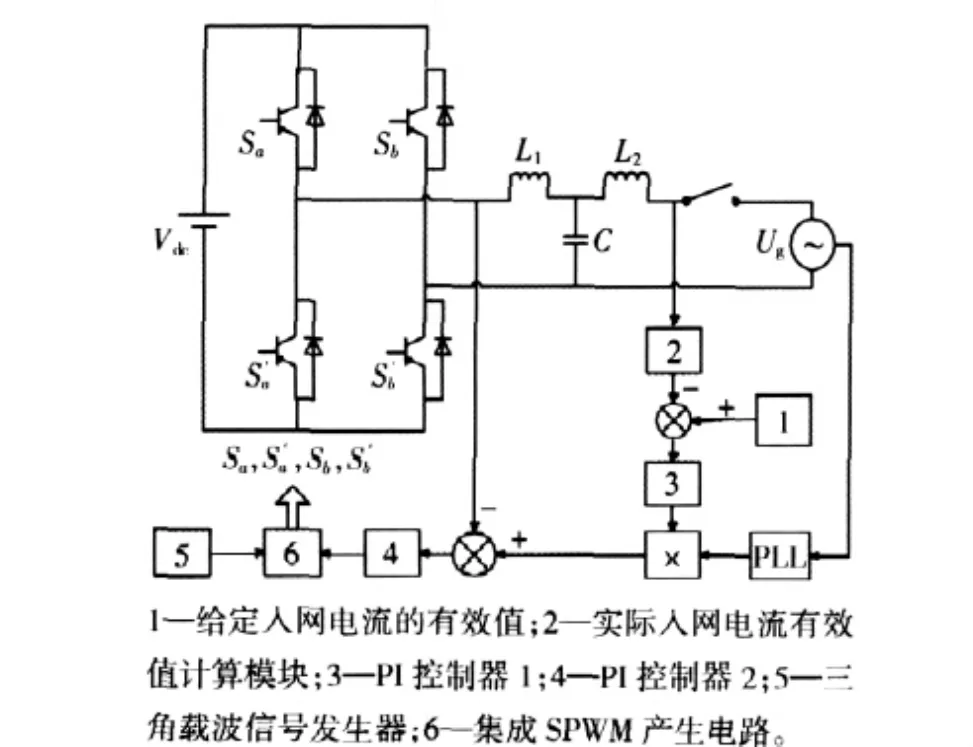
圖1 單相并網逆變電源系統Fig.1 System of single phase grid-connected inverter

假設當逆變橋臂上開關開通，橋臂下開關管關斷時，有

當橋臂上開關關斷，橋臂下開關管開通時，有

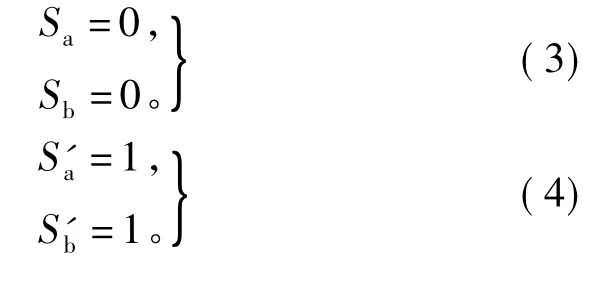
則并網逆變器的開關函數模型可表示為

那么，并網逆變器系統功率電路的開關函數模型可以描述為

根據疊加原理，分別考慮Uab(s)與Ug(s)對橋臂輸出電流I1(s)和輸入電網電流I2(s)的傳遞函數為

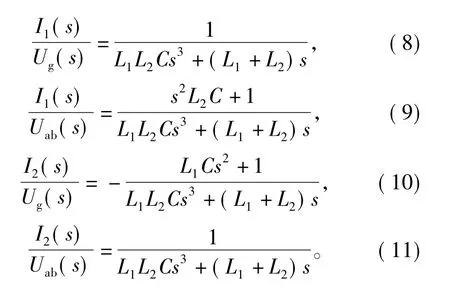
由上述并網逆變電源的數學模型可知，直接入網電流I2(s)與橋臂輸出電壓Uab(s)的傳函為三階函數，如果選擇直接控制I2(s)，則系統是一個不穩定系統［1－3］。為了改善系統的穩定性，本文首先采集電網側電感的電流，通過整流濾波后求出其有效值，然后采用直接入網電流的有效值作為控制器的外環，即外環給定為入網電流的有效值，把外環的誤差經過PI運算后，再與鎖相環所得到的電網電壓相位基準相乘后作為橋臂側輸出濾波電感電流瞬時值的給定值，從而形成一個并網電流的雙閉環控制策略，以增加系統阻尼，增強系統的穩定性。并且給出了該控制策略下系統的控制框圖。

2 控制策略的原理分析

并網逆變電源控制的終極目的就是控制直接饋網電流的幅值和相位，使饋入電網的電流符合一定的標準。本文選擇實際饋網電流的有效值作為外環，把橋臂輸出電流作為內環，構成雙閉環控制系統，如圖2所示，既直接控制了饋網電流的幅值，又能使并網電流的相位滿足要求，這樣即保證了并網電流的穩態波形質量，又具有較高的控制精確度。

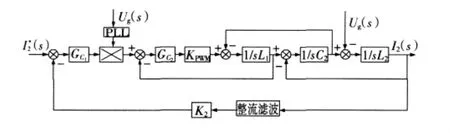
圖2 并網逆變器雙閉環控制系統框圖Fig.2 Block diagram of dual-loop controller with RMS of i2and i1feedback

2.1 穩定性分析

系統內環采用比例控制GC2=K，外環采用PI控制，GC1=KP+KI/s。為方便分析系統的穩定性，利用控制原理中控制框圖等效變換的原則，對圖2進行等效變換后得到如圖3所示的控制框圖。

圖3 基于i2和i1的雙閉環控制等效結構框圖Fig.3 Equivalent block diagram of i2and i1dual-loop control system

從控制框圖3可以看出，饋網電流不但受逆變器側電壓控制，而且與不可控制量Ug有關，如果不考慮Ug的影響，又因為系統的反饋系數看作常數時不影響系統的穩定性，所以這里為了研究系統穩定性，假設反饋系數為1，則圖3的開環傳遞函數為

為了便于分析和設計，畫出KI=0，KP變化時系統的根軌跡如圖4所示。明顯可以看出此系統是一個條件穩定系統，即該系統控制器的控制參數設計必須在某一區間才能確保系統是穩定的。

圖4 雙閉環控制系統的根軌跡Fig.4 Root locus of dual-loop control system

2.2 內環參數設計

由上述分析可得內環的開環傳遞函數為

顯然式(15)所標示的系統為一個穩定系統，被控系統是一個三階系統，其中T型濾波器的諧振頻率為

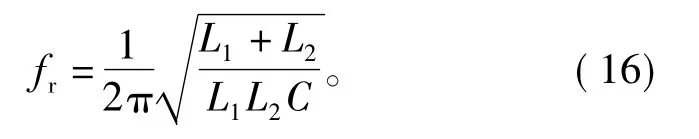
為了便于設計，本文內環使用比例控制，即GC2(s)=K，理論上K值的大小并不影響內環系統的穩定性，只影響系統的動態性能，由式(14)可知K對整個系統的穩定性有影響，又因為開環特征方程的阻尼系數

工程上常取0.6＜ζ＜0.8，如果取最佳阻尼比，即ζ=0.707，在主電路參數確定的情況下，即可計算出K值，這里在仿真試驗的基礎上取K=100。

2.3 外環參數的設計與分析

在進行有效值外環設計時，可以把內環看作一個被控對象，此時其控制框圖可等效為圖5。在實驗時由于實際系統的參數存在離散性，所以系統控制器的設計必須保留一定的相角和幅值裕度，通常工程上取相角裕度 γ為45°～60°，幅值裕度 h為5～10dB。

根據式(14)的穩定條件，要選擇一組合適的KP、KI參數，工程上有多種整定方法，本文采用振蕩法結合系統的開環Bode圖，并且綜合考慮系統的帶寬和穩態特性來設計外環控制器的參數，選擇KP=0.5，KI=100作為系統的控制器參數較為理想，此時的γ=68°

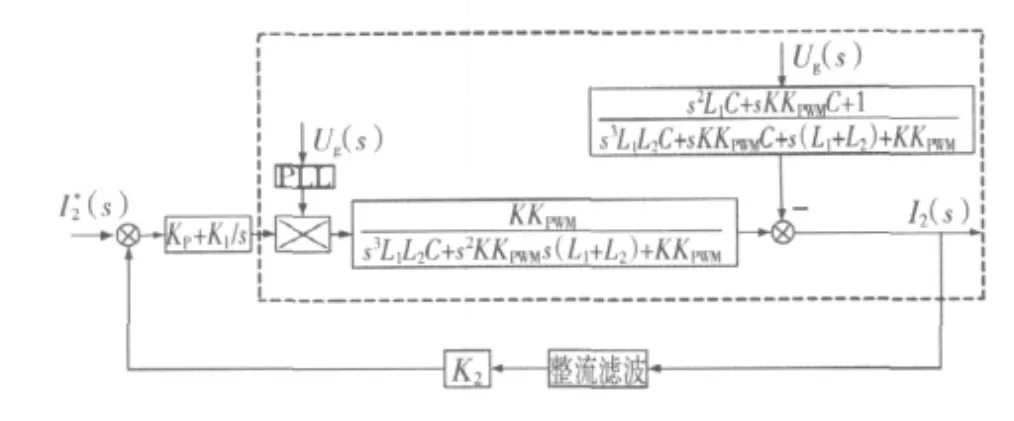
圖5 外環控制等效結構框圖Fig.5 Equivalent block diagram of out-loop control system

3 仿真研究

為了驗證所提出的控制方案的正確性，在Matlab/SIMULINK環境中對系統進行仿真，仿真參數:L1=2 mH，L2=1 mH，C=2 μF，Vdc=400 V，Ug=311sin(100πt)V，開關頻率 fs=10 kHz，圖6、圖7 分別是KP=0.5，KI=100時使用本文提出的雙閉環控制策略下給定并網電流有效值為6A的穩態波形和并網電流有效值從6 A突變到3 A，再變到6 A時的動態仿真波形。為了能直觀且清晰地看出并網電流和電網電壓之間的相位關系，把所有仿真波形中的電壓都進行了標準化處理，本文把電壓衰減到10 V，電流取實際值。從波形圖上可以看出，系統的并網電流不僅具有良好的穩態特性，而且在電流給定突變的情況下仍能穩定運行，且具有較快的動態性能。

4 實驗驗證

本文采用DSP320LF2812作為核心控制器件，研制了一臺1kVA的并網逆變器原理樣機如圖8所示，以進一步驗證上述并網逆變器的控制策略，通過自藕變壓器進行并網實驗。

圖8 系統硬件框圖Fig.8 The hardware frame of system

圖9為采用本文所提雙閉環控制時的穩態饋網電流和電壓的實驗波形，此時，饋網電流的總諧波畸變率為1.9%，并網電流功率因數為0.995。應用本文所提的雙閉環控制時，并網電流有效值由5A突變到3A時的動態實驗波形如圖10所示，實驗結果表明采用本文所提的控制策略下的并網逆變器，具有良好的穩態和動態性能。

5 結語

為提高并網逆變器饋網電流的波形質量和并網功率因數，本文針對LCL濾波的并網逆變器單獨采用并網電流單閉環直接控制時系統存在諧振尖峰，易造成系統不穩的特點，提出采用饋網電流有效值作為外環，橋臂電流瞬時值作為內環的雙閉環控制策略;建立了系統的控制模型，證明了該系統是一個條件穩定系統，且根據Routh-Hurwitz穩定判據推出了系統穩定條件。通過仿真和實驗驗證了上述控制策略的有效性。

［1］ KIM Hyosung，YU Taesik，CHOI Sewan.Indirect current control algorithm for utility interactive inverters in distributed generation systems［J］.IEEE Transactions on Power Electronics，2008，23(3):1342－1347.

［2］ BOLSENS B，DE BRABANDERE K，VAN DEN KEYBUS J，et al.Model-based generation of low distortion currents in grid-coupled PWM inverters using an LCL output filter［J］.IEEE Transactions on Power Electronics，2006，21(4):1032 －1040.

［3］ TWINING E，HOLMES D G.Grid current regulation of a threephase voltage source inverter with an LCL input filter［J］.IEEE Transactions on Power Electronics，2003，18(3):888 －895.

［4］ GONZALEZ R，LOPEZ J，SANCHIS P，et al.Transformerless inverter for single-phase photovoltaic systems［J］.IEEE Transactions on Power Electronics，2007，22(2):693 －697.

［5］ JAIN S，AGARWAL V.A single-stage grid connected inverter topology for solar PV systems with maximum power point tracking［J］.IEEE Transactions on Power Electronics，2007，22(5):1928－1940.

［6］ KOJABADI H M，YU Bin，GADOURA I A，et al.A novel DSP-based current controlled PWM strategy for single phase grid connected inverters［J］.IEEE Transactions on Power Electronics，2006，21(4):985－993.

［7］ 胡雪峰，譚國俊.SPWM逆變器復合控制策略［J］.電工技術學報，2008，23(4):88－92.

HU Xuefeng，TAN Guojun.The multiple control strategy for SPWM inverter［J］.Transactions of China Electrotechnical Society，2007，22(9):43－47.

［8］ 陳瑤，金新民，童亦斌.三相電壓型PWM整流器網側LCL濾波器［J］.電工技術學報，2007，22(9):124－129.

CHEN Yao，JIN Xinmin，TONG Yibin.Grid-side LCL-filter of three-phase voltage source PWM rectifier［J］.Transactions of China Electrotechnical Society，2007，22(9):124－129.

［9］ 胡雪峰，譚國俊.應用神經網絡和重復控制的逆變器綜合控制策略［J］.中國電機工程學報，2009，29(6):43－47.

HU Xuefeng，TAN Guojun.Integrated control strategy for inverters based on neural network and repetitive control［J］.Proceedings of the CSEE，2009，29(6):43－47.

［10］ 楊勇，索跡，祁春清，等.三相并網逆變器電感在線辨識控制［J］.電機與控制學報，201，15(3):52－57.

YANG Yong，SUO Ji，QI Chunqing，et al.Inductance online identification control for three-phase grid-connected inverters［J］.Electric Machines and Control，2011，15(3):52 －57.

［11］ 魏永清，張曉鋒，喬鳴忠.采用參考電壓調節的并聯逆變器控制技術［J］.電機與控制學報，2011，15(2):84－88.

WEI Yongqing，ZHANG Xiaofeng，QIAO Mingzhong.parallel control technique of multiple inverters based reference voltage regulation［J］.Electric Machines and Control，2011，15(2):84－88.

(編輯:張詩閣)

Study on control scheme for grid-connected inverter with LCL filter

DENG Xiang1， HU Xue-feng1，2， GONG Chun-ying1
(1.College of Automation Engineering，Nanjing University of Aeronautics ＆ Astronautics，Nanjing 210016，China;
2.Key Laboratory of Power Electronics and Motion Control of Anhui，Anhui University of Technology，Ma’anshan 243002，China)

Only single grid current closed loop is not sufficient for the stability of the grid-inverter with LCL filter.This paper proposed a dual-loop control strategy with grid current root-mean-square(RMS)and leg output current，where grid current RMS is out feedback loop，and leg output current is inner feedback loop.It verified the stability of system by using Routh-Hurwitz criterion，and system modeling and stability analysis were also presented.The proposed control scheme was verified by simulation results and experiments on a 1kVA grid-connected photovoltaic inverter based on DSP.The results show that the proposed scheme can ensure the stability of the system and the grid current performances，and achieve fast transient responses.

grid-inverter;LCL filter;control scheme;system modeling;stability

TM 464

A

1007－449X(2011)05－0037－05

2010－09－01

國家重點基礎研究發展計劃(973計劃)資助項目(2007CB210303)

鄧 翔(1973—)，男，高級工程師，研究方向為功率電子變換技術;

胡雪峰(1973—)，男，博士研究生，副教授，研究方向為新能源發電技術、電力電子與電力傳動;

龔春英(1965—)，女，教授，博士生導師，研究方向為電力電子與電力傳動、新能源發電技術。