基于粒子群算法的油品調和調度優(yōu)化研究

唐國維,趙 雪

(東北石油大學計算機與信息技術學院,黑龍江大慶163318)

在煉油生產過程中,油品調和是一項重要工序[1]。近些年,國內對于高標號汽油的各種環(huán)保油品的需求較多,而大多數(shù)煉油廠用現(xiàn)行技術生產的成品油一次合格率不高,不能滿足用戶的需求。曹萃文等[2]引入油品非線性調和模型,提出了集成控制原油線性調和、基于訂單的短期生產計劃、成品油非線性調和及庫存管理的算法;王繼東等[3]采用遺傳算法解決油品調和調度問題;趙小強[4]針對該調和問題給出了一種基于基本微粒群算法的解決方法,但粒子群算法收斂速度較慢且容易陷入局部極值點。下面,筆者引入一種動態(tài)改變權重的粒子群優(yōu)化算法,對煉油企業(yè)生產調度的油品調和決策進行了研究。

1 成品油調和優(yōu)化模型的建立

煉油生產裝置規(guī)模龐大,工藝復雜,影響煉油生產的參數(shù)和變量繁多。筆者結合煉油工藝和某煉油廠實際生產情況,選取對煉油生產有決定意義裝置的變量和參數(shù)作為決策量。一般油品調和模型以費用最低為目標。油品調和模型[5]可歸結為數(shù)學規(guī)劃問題。目標函數(shù)由調和產品的價值、調和組分的價值及調和操作費用組成。其目標函數(shù)為:

式中,Pi(i=1,…,I)表示調和產品的種類;Cj(j=1,…,J)表示調和組分的種類;t(t=1,…,T)表示時間間隔長度;BCj,t、B Pi,t分別為Cj和Pi的生產量;D Pi,Cj為Cj調和成Pi的成本;F為調和產品利潤;GPj為Pi的單位市場價;GCj為Cj的單位市場價;λPi,Cj=0或 1,表示是否有參與調和。

約束條件包括如下內容:①產品的生產量約束(min B Pi,t≤BPi,t≤max BPi,t),min BPi,t、max BPi,t分別為BPi,t的最小和最大生產量;②產品和調組份平衡關系;③產品庫存量平衡關系(VPi,t=V Pi,i-1+BPi,t-XPi,t),XPi,t為P i的需求量;VCj,t、VPi,t分別為Cj和P i的庫存量;④產品的庫存量約束分別為VPi,t最小和最大庫存量;⑤產品的質量滿足(Qm,Pi,t=f q(BPi,Cj,t,Qm,Cj,t,NPi,Cj,t)),NPi,Cj,t為Cj用于P i的比例,BPi,Cj,t為Pi所用的Cj的生產量,Qm(m=1,…,M)表示調和產品屬性種類;Qm,Cj,t、Qm,Pi,t分別為Cj和Pi的屬性值;⑥產品質量約束(min Qm,Pi≤Qm,Pi,t≤max Qm,Pi),min Qm,Pi、max Qm,Pi分別為Qm,Pi,t的屬性的最小值和最大值;;⑧組份庫存量約束(min VCj,t≤VCj,t≤max VCj,t),min VCj,t、max VCj,t分別為VCj,t的最小和最大庫存量;⑨組份質量滿足(min Qm,Cj≤Qm,Cj,t≤max Qm,Cj),min Qm,Cj和⑦組分庫存量滿足max Qm,Cj為Qm,Cj,t屬性的最小和最大值;⑩調和組份滿足

在調和模型中,對約束條件的處理很重要。為此,筆者采用罰函數(shù)方法,把優(yōu)化計算中約束優(yōu)化問題轉化為無約束優(yōu)化求解。對于非線性油品調和優(yōu)化問題采用了如下罰函數(shù):

式中,qi(x)=max{0,gi(x)};Q(qi(x))為多段賦值函數(shù),Q(qi(x))的選取規(guī)則為Q(qi(x))=10(qi(x)＜1)或Q(qi(x))=100(qi(x)≥1);r(qi(x))為罰函數(shù)的冪函數(shù),r(qi(x))的選取規(guī)則為r(qi(x))=1(qi(x)＜1)或r(qi(x))=2(qi(x)≥1);h(x)為Rn上的連續(xù)函數(shù)。

2 粒子群算法描述

粒子群優(yōu)化算法 (PSO)是一種基于群體智能的優(yōu)化技術[6],其從隨機解出發(fā),通過迭代尋找最優(yōu)解,通過適應度來評價解的品質,通過追隨當前搜索到的最優(yōu)值來尋找全局最優(yōu)。

油品調和是直接影響煉油廠經濟效益的一個關鍵環(huán)節(jié)。在油品調和過程中,成品油性質指標通常是組分性質的非線性函數(shù)。筆者在基本粒子群算法的基礎上,動態(tài)改變慣性權重[7],使迭代中的慣性權重ω隨粒子的位置和目標函數(shù)的變化而變化。

在粒子群算法中,假設Xi=(x i1,xi2,…,xiD)T表示第i個粒子,其中D是粒子的維數(shù)。其經歷的最好位置表示為Pi=(pi1,pi2,…,piD)T,而整個群體經歷的最好位置表示為Pg=(pg1,pg2,…,pgD)T,粒子i的速度為Vi=(vi1,v i2,…,v iD)T。按追隨當前最優(yōu)粒子的原理,粒子i將按式(3)改變速度,式(4)改變位置[8]:

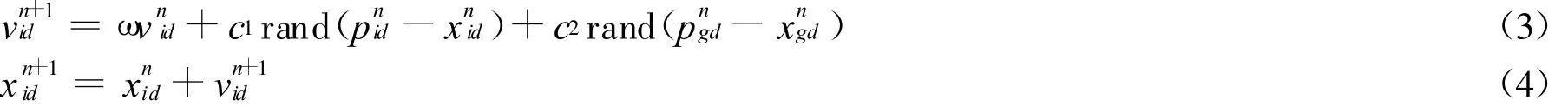
式中,n為當前的進化代數(shù);c1、c2為學習因子;rand()為分布于(0,1)的隨機數(shù)。

采用粒子平均維間距來描述種群的維多樣性。設S為種群粒子數(shù)目,xid為第i個粒子在第d維上的值,ˉx d表示所有粒子第d維上坐標值均值,則定義第d維的種群多樣性為:

式(5)用平均維間距M(d)描述了種群某一維粒子相互之間分布的離散程度,設定ω=0.8。在多樣性最差、某一維所有點聚集在一起時,可設定ω=0.1進行精細的開發(fā)。因此,得到ω的計算公式:

式中,K為壓縮因子,在 (0,1)間取值。具體算法的步驟如下:①設定算法相關參數(shù)值;②初始化種群中每個粒子的位置和速度;③評價每一個粒子,更新粒子的最優(yōu)位置與群體的最優(yōu)位置;④采用上述方法動態(tài)調整慣性權重值,并按式 (3)和式 (4)更新粒子的位置和速度;⑤判斷算法是否滿足中止條件,若滿足則算法結束;否則,轉回式 (6)。

3 成品油調和優(yōu)化過程的實現(xiàn)

以某煉油廠汽油調和為例,一重催、二重催生產的組份汽油,經過加入少量的重整汽油、乙烯芳烴和MTBE,就可以調和成各種牌號的乙醇汽油組份油。組分油和成品油的性能指標如表1和表2所示。

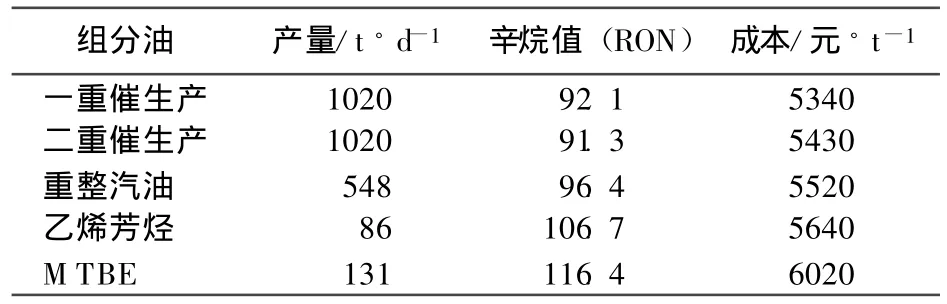
表1 組分油性能指標

表2 成品油性能指標

調和乙醇汽油組分油90#、93#、97#的產量分別為X 1、X 2、X3;調和乙醇汽油組分油90#使用一重催生產的組分汽油、使用二重催生產的組分汽油、重整汽油、乙烯芳烴、MTBE的量分別為X 11、X 12、X 13、X14、X 15;93#使用一重催生產的組分汽油、使用二重催生產的組分汽油、重整汽油、乙烯芳烴、MTBE的量分別為X 21、X 22、X23、X 24、X 25;97#使用一重催生產的組分汽油、使用二重催生產的組分汽油、重整汽油、乙烯芳烴、MTBE的量為 X31、X32、X33、X34、X35。

則:

物料平衡約束為:

收入量約束為:

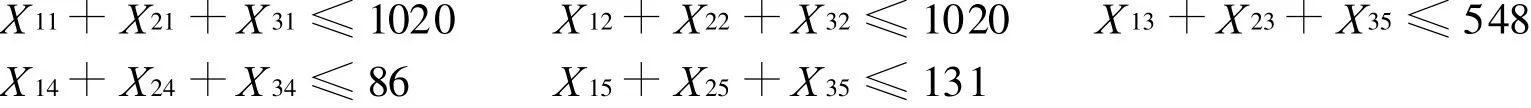
產量約束為:

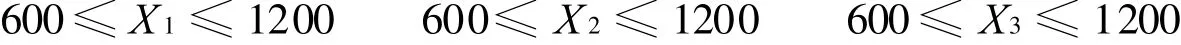
辛烷值約束為:

為了方便比較各算法的性能,將相關參數(shù)設置如下:①基本粒子群算法中,c1=c2=2;慣性權重因子ω采用線性遞減的方式從0.9減少到0.4。②在筆者引入的改進算法中,c1=c2=1.62;慣性權重按式(6)進行動態(tài)調整。2種算法分別進行最大迭代次數(shù)為G=1500和2000,種群規(guī)模P=40和80。為了減少偶然性的影響,在迭代次數(shù)相同的條件下,各算法測試均運行50次,然后取平均值。其結果如表3所示。

從表3可以看出,與基本算法相比,通過改進算法得到的調和成品油的利潤提高了10400元。這是因為改進算法略微加快了算法的收斂速度,同時有利于跳出局部極值,具有較好的全局搜索能力,從而保證了乙醇汽油的質量,使煉油廠的經濟效益得到提高。

表3 算法計算結果比較

4 結 語

結合煉油廠實際生產情況,選取有決定意義的裝置的變量和參數(shù),建立油品調和模型,以煉油廠最大利潤為目標,引入改變權重的粒子群優(yōu)化算法來解決,既保證了尋優(yōu)過程中粒子群體的多樣性,又加快了算法的全局收斂能力,保證了產品的質量,使煉油廠效益得到提高。因此,粒子群優(yōu)化算法對煉油廠改進油品調和調度方法、實施調和調度優(yōu)化有現(xiàn)實意義。

[1]蔡智.油品調和技術-煉油工業(yè)技術 [M].北京:中國石化出版社,2006.

[2]曹萃文,顧幸生.非線性油品優(yōu)化調和在煉油廠中的應用 [J].化工自動化及儀表,2005,32(6):12-15.

[3]王繼東,王萬良.基于遺傳算法的汽油調和生產優(yōu)化研究 [J].化工自動化及儀表,2005,32(1):6-9.

[4]趙小強,榮岡.基于微粒群優(yōu)化算法的不確定性調和調度 [J].中國化學工程學報,2005,13(4):535-541.

[5]薛美盛,李祖奎,吳剛,等.成品油調和調度優(yōu)化模型及其應用 [J].石油煉制與化工,2005(11):64-48.

[6]Kennedy J,Eberhart R C.Partical Swarm Optimization[A],Proceeding of the 1995 IEEE International Conference on Neural Network[C].Perth,Australia,1995:1942-1948.

[7]王啟付,王戰(zhàn)江,王書亭.一種動態(tài)改變慣性權重的粒子群優(yōu)化算法 [J].中國機械工程,2005,16(11):945-948.

[8]龍文,梁昔明,董淑華,等.動態(tài)調整慣性權重的粒子群算法 [J].計算機應用,2009,29(8):2240-2242.