有限部分變換半群的幾類平凡子半群

秦美青

(菏澤學(xué)院數(shù)學(xué)系,山東菏澤274015)

設(shè)X是集合,集合X上的所有部分變換在一般映射的合成運算下做成的半群稱為部分變換半群[1],記為PX。下面,筆者主要給出當集合X是有限集時,部分變換半群RX的子半群S為R-平凡子半群、L-平凡子半群、J-平凡子半群的充要條件。

1 基本概念

定義1[2]設(shè)S為半群,ρ為S上的等價關(guān)系,若對每個a,b∈S,aρb?a=b,則等價關(guān)系ρ稱為平凡的。

定義2[3]設(shè)S為半群,若對每個a∈S,存在m,r∈IN,使得am+r=am,則稱半群S為周期的,特別地,若對每個a∈S,r=1,則半群S稱為非循環(huán)的。

引理1[4]設(shè)S是一個周期半群,則:

1)S是R-平凡的當且僅當對每個a,b∈S,存在m ∈IN,使得(ab)ma=(ab)m。

2)S是L-平凡的當且僅當對每個a,b∈S,存在m∈IN,使得(ab)m=b(ab)m。

3)S是J-平凡的當且僅當對每個a,b∈S,存在m ∈IN,(ab)ma=(ab)m=b(ab)m。

2 主要結(jié)果

2.1 PX的R-平凡子半群

設(shè)S是PX的子半群,α∈ PX。Fix(α)={x ∈ domα,|xα=x},Fix(S)={Fix(α)|α∈ S}。

定理1 設(shè)S是PX的子半群,則S是R-平凡的當且僅當對每個α,β∈S,有Fix(αβ)=Fix(α)∩Fix(β)。

證明 設(shè)S是R-平凡的。因為X是有限集,所以S是周期半群。任取 x∈ Fix(αβ),則x∈dom(αβ)。由 dom(αβ)=(imα∩ domβ)α-1?domα,故 x ∈ domα。因為 x ∈ Fix(αβ),所以 x=xαβ∈ dom(αβ),這樣 x=xαβ=(xαβ)αβ=x(αβ)2,又因為 x=x(αβ)2∈ dom(αβ),所以 x=xαβ=[x(αβ)2]αβ=x(αβ)3,依次類推有 x=xαβ =x(αβ)m,再由引理 1 知 x=xαβ =x(αβ)m=x(αβ)mα=xα,即 x ∈ Fix(α)。因為x=xα且xα∈ domβ,所以 x=xαβ=xβ,即 x ∈ Fix(β)。從而對任意 x ∈ Fix(αβ),有 x ∈ Fix(α)且 x ∈Fix(β),故 Fix(αβ)?Fix(α)∩ Fix(β)。

任取 x ∈ Fix(α)∩ Fix(β),則 x ∈ domα∩ domβ且xβ =x=xα∈ domβ,這樣 xαβ =xβ =x,即x ∈ Fix(αβ),故對任意 x ∈ Fix(α)∩ Fix(β),有 x ∈ Fix(αβ),從而Fix(α)∩ Fix(β)?Fix(αβ),這樣就有Fix(αβ)=Fix(α)∩ Fix(β)。

反之 ,設(shè) α,β ∈ S 且 αRβ,則存在 γ,δ∈ S,使得 α=βγ,β=αδ。因為:所以 domα=domβ。任取 x ∈ domα=domβ,則 xα=xαδγ,即 xα∈ Fix(δγ)。再由對每個 α,β∈ S,有Fix(αβ)=Fix(α)∩ Fix(β),故 xα=Fix(δ)∩ Fix(γ),從而 xα=(xα)δ=xβ,即對任意 x ∈ domα=domβ有 xα=xβ,從而 α=β,故S 是R-平凡的。

2.2 PX的L-平凡子半群

定義3[5]設(shè)α∈PX,則由等價關(guān)系W(α)={(x,y)∈domα×domα|xαs=yαt,對某個s,t≥0}確定的等價類稱為α的軌跡。α的所有軌跡做成的集合記為Ψ(α)。

定義4[6]設(shè) Xi∈ Ψ(α),集合{x ∈ Xi|xαr=x,對某個r＞0}稱為 Xi的kernel,記為K(Xi)。

定理2 設(shè) α∈PX,則 α是非循環(huán)的當且僅當對每個Xi∈ Ψ(α),|K(Xi)|=1。

證明 設(shè) α∈PX是非循環(huán)的。任取x∈K(Xi),由K(X i)得定義知,存在 s＞0,使得 xαs=x,則(xαs)αm+1-s=xαm+1-s,從而 xαm+1=(xαm)α1-s,因為 α是非循環(huán)的 ,所以 xαm+1=xαm,則s=1,故 xα=x。若存在y ∈ K(Xi),則 x,y ∈ Xi?Ψ(α),即存在s1,s2 ＞0,使得 x=xα=…xαs1-1=xαs1=yαs2=yαs2-1=… =yα=y,從而|K(Xi)|=1。

反之,假設(shè)對每個Xi∈ Ψ(α),|K(Xi)|=1。因為|K(Xi)|=1,所以任意 x ∈ K(Xi),有 x=xα,否則 ,存在 r ＞0,使得 xαr=x,這樣 xαr+1=xα,即(xα)αr=xα,從而 xα∈ K(X i)與|K(Xi)|=1矛盾 。對任意 x ∈ K(X i),顯然存在m,使得xαm+1=xαm,不妨設(shè)m充分大。任取 y且滿足(x,y)∈ W(α),則存在 s,t ＞0,使得 xαs=yαt。

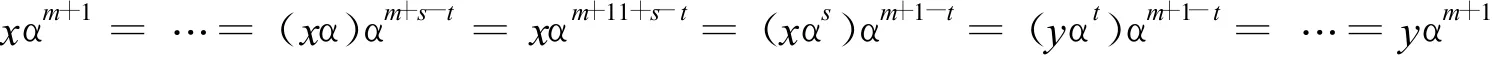
相似可證 ,xαm=yαm。因為 xαm=xαm+1,所以 yαm=yαm+1,故 αm=αm+1,從而 α∈ P X 是非循環(huán)的。

從定理2容易得出若α是非循環(huán)的,則(x,y)∈W(α),當且僅當 xαm=yαm,其中,m為充分大整數(shù)。

定理3 設(shè)S是P X的子半群,則S是L-平凡的當且僅當對每個α,β∈S,有W(αβ)=W(α)∨ W(β)。

證明 在整個證明過程中m表示充分大整數(shù)。假設(shè)S是L-平凡的,則S是非循環(huán)的且對每個α,β∈S,有(αβ)m=β(αβ)m。設(shè)(x,y)∈ W(αβ),則 x,y ∈ dom(αβ)?domα且 x(αβ)m=y(αβ)m。因為S 是非循環(huán)的且 x ∈ domα,xα∈ domβ,所以 xαm+1=xαm,即(xα)αm=xαm,故(x,xα)∈ W(α)。因為(xα)βm=(xα)βm+1=(xαβ)βm,所以(xα,xαβ)∈ W(β)。因為(xαβα)αm=(xαβ)αm+1=(xαβ)αm,所以(xαβ,xαβα)∈W(α)。依次類推有(x(αβ)m-1α,x(αβ)m)∈ W(β)。這樣就有(x,x(αβ)m)∈ W(α)∨ W(β)。相似可證(y,y(αβ)m)∈ W(α)∨ W(β)。因為 x(αβ)m=y(αβ)m,所以(x,y)∈ W(α)∨ W(β),從而 W(αβ)?W(α)∨W(β)。因為 x ∈ dom(αβ)m=domβ(αβ)m=dom(βα)mβ ?dom(βα)m且S 是非循環(huán)的子半群,所以(βα)m=(βα)m+1,故 x ∈ dom(βα)m+1。進一步有 x(βα)m+1=xβ(αβ)mα=x(αβ)mα=y(αβ)mα=y(βα)m+1,故(x,y)∈ W(βα),從而 W(αβ)?W(βα)。相似可證 W(βα)?W(αβ),這樣就有 W(βα)=W(αβ)。不妨設(shè) x,y ∈dom(αβ)m=domβ(αβ)m?domβ,且(x,y)∈ W(β),則 x(αβ)m=xβ(αβ)m=xβm(αβ)m=yβm(αβ)m=y(αβ)m,這樣有(x,y)∈ W(αβ),從而 W(β)?W(αβ)。相似可證 W(α)?W(βα)=W(αβ),故 W(α)∨W(β)?W(αβ),這樣就有 W(αβ)=W(α)∨ W(β)。

反之 ,假設(shè)對每個 α,β ∈ S,有W(αβ)=W(α)∨ W(β),則 W(α)=W(α2)=W(α3)= …,從而 S 是非循環(huán)的。事實上,若對任意 x ∈ domα,有 xαr=x且xα≠x,則對每個 s,t≥0,有 x(αr)s=x ≠xα=xα(αr)t,這樣有(x,xα)∈ W(α)但(x,xα)? W(αr)與 W(α)=W(αr)矛盾。因為對每個 x ∈ domβ和每個 α,β∈ S 有(x,xβ)∈ W(β)?W(αβ),則 x ∈ dom(αβ)m且又因為S 是非循環(huán)的,所以對每個 x ∈dom(αβ)m,有 x(αβ)m=xβ(αβ)m,即(αβ)m=β(αβ)m,故 S 是L-平凡的 。

2.3 PX的J-平凡子半群

定理4 設(shè)S是P X的子半群,則S是J-平凡的當且僅當對每個α,β∈S,有:

證明 首先說明因為X是有限集,所以S是有限半群,從而是周期半群,故在S上J=D。

假設(shè)S是J-平凡的。任取α,β∈S且αRβ,則αJβ。因為S是J-平凡的,從而α=β,故S是R-平凡的,由定理 2知 Fix(αβ)=Fix(α)∩ Fix(β)。相似可證 ,任取α,β∈ S 且αLβ,則 αJβ。因為 S 是J-平凡的,從而α=β,故 S 是J-平凡的,由定理3知 W(αβ)=Fix(α)∩ Fix(β)。

反之 ,假設(shè)每個 α,β∈ S,有 Fix(αβ)=Fix(α)∩ Fix(β),W(αβ)=Fix(α)∩ Fix(β),任取 α,β∈ S,且αJβ ,則存在 γ∈ S,使得 αRγ,γLβ,由假設(shè)知,Fix(αβ)=Fix(α)∩ Fix(β),W(αβ)=Fix(α)∩ Fix(β)。再由定理2和定理3知α=β=γ,從而S是L-平凡的。

[1]Saito T.J-trivial subsemigroupsof finite full transfirmation semigroups[J].Semigroup Forum,1998,57:60-68.

[2]How ie J M.P roudu ctsof idem potent in finite full transformation sem igroups[J].Proc Royal Soc Edinburgh A,1980,86:243-254.

[3]Umar A.On the sem igroups of order-decreasing finite full transformations[J].Proc Royal Soc Edinburgh A,1992,120:129-142..

[4]How ie J W.An introduction to sem igroup Theory[M].London:Academ ic Press,1976.

[5]秦美青,許新齋.關(guān)于部分變換半群的一類子半群 [J].山東師范大學(xué)學(xué)報 (自然科學(xué)版),2009,24(1):6-9.

[6]許新齋,許四軍,毛娟,等.關(guān)于序半群的結(jié)構(gòu)與理想[J].山東師范大學(xué)學(xué)報(自然科學(xué)版),2008,23(1):4-6.