一類新的6維李代數及其相關的Liouville可積哈密頓系統＊

郭福奎,馮濱魯,魏 媛,張玉峰

(1.山東科技大學,山東 青島 266510;2.濰坊學院,山東 濰坊 261061; 3.濱州學院,山東 濱州 256600;4.中國礦業大學,江蘇 徐州 221116)

1 引言

近年來可積系統理論有了迅速的發展,文獻[1-4]中給出了尋求可積系統的方法。其中一種方法是著名的Lax法,它是由屠規彰教授提出的[5],后來稱之為屠格式。在本文中我們將利用屠格式得到新的可積系統。因此,我們簡單的介紹一下屠格式。

設G是數域C上的矩陣李代數。令G=G?C(λ,λ-1)是其相應的loop代數,其中 C(λ,λ-1)表示一組關于參數λ的洛朗多項式。G中基元的階數可定義為deg(x?λn)=n,x∈G。

首先,記靜態零曲率方程

的解為V=V(λ),且Vx(n)=(λnV)++Δn滿足

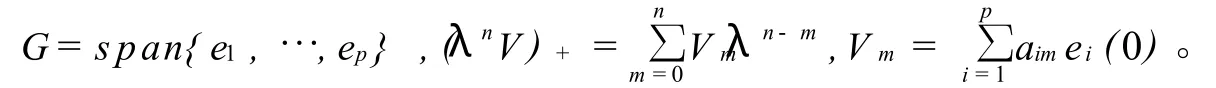
其次,利用零曲率方程

可以得到Lax可積方程族

最后,根據方程(1)我們可以得到哈密頓算子J和循環算子L,因此方程(4)可以寫成哈密頓形式

其中 Hn(n∈Z)表示方程(5)的守恒密度,可以由跡恒等式[5]

計算得到,其中〈A,B〉表示矩陣的跡,例如〈A,B〉=tr(AB),?A,B∈G。由文獻[5]的論述可知,如果JL =L＊J,那么Lax可積方程族(4)是Liouville可積的。

可積系統一個重要的擴展方向是可積耦合,可積耦合是在文獻[6-7]提出的,并作了相關的研究。對可積耦合的研究不僅可以幫助我們探討可積系統的對稱,還可以幫助我們發現不同進化方程的可積方程族之間的關系。例如在文獻[8]中我們構造了一個可積模型(實際上是可積耦合)把著名的A KNS方程族和KN方程族聯合在一起。郭福奎教授和張玉峰教授在文獻[9]中提出一種簡便有效地推導可積耦合的方法,其要求李代數G可以分解成兩個直和子代數G1,G2它們滿足

其中⊕表示直和,[,]表示李括號。自然我們會想到探討可積耦合的一些性質,例如哈密頓結構。然而利用跡恒等式(6)是得不到哈密頓結構的。因此,我們提出一種有效的工具即二次型恒等式[10]來得到可積耦合的哈密頓結構。這個恒等式是推廣的跡恒等式,也就是說跡恒等式是二次型恒等式的一種特殊的情形。為了便于閱讀本文,我們先來回顧一下二次型恒等式。

其中 a,b∈G,F=(fij)s×s是常數對稱矩陣。我們要求(8)滿足以下關系

其中U,V滿足Vx=[U,V],Λ∈G。關于W的兩個約束條件為

我們可以得到

都是方程(1)的解,所以存在常數滿足

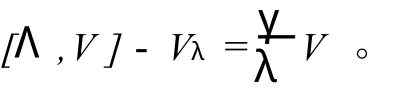
由(15)可以推導出二次型恒等式

本文中,介紹了一類新的6維李代數V6,其具有顯著的特點,例如它不滿足關系式(7)。因此,利用V6和屠格式所生成的可積系統不是可積耦合。下面,我們會推導出兩類新的進化方程的Liouville可積方程族并根據二次型恒等式得到它們的哈密頓結構。

2 一類新的李代數和兩類可積方程族

設

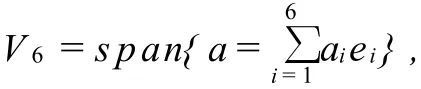
其中ei(i=1,2,3,4,5,6)為V6的一組基,并滿足下面的換位運算

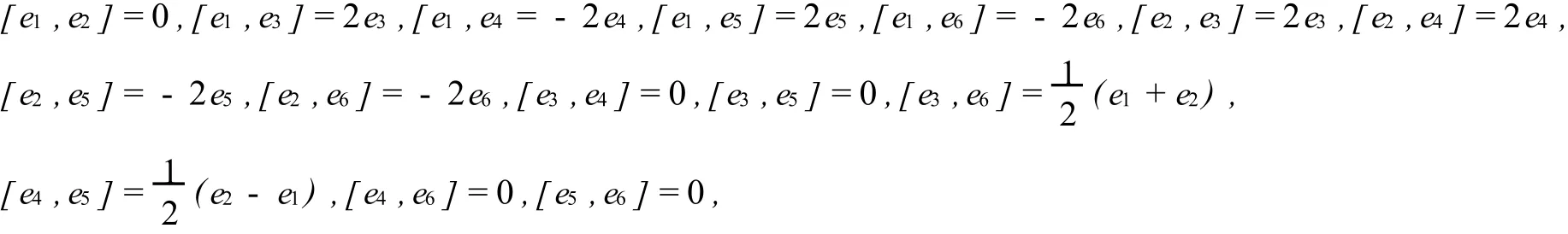
其中[a,b]=ab-ba,a,b∈V6。

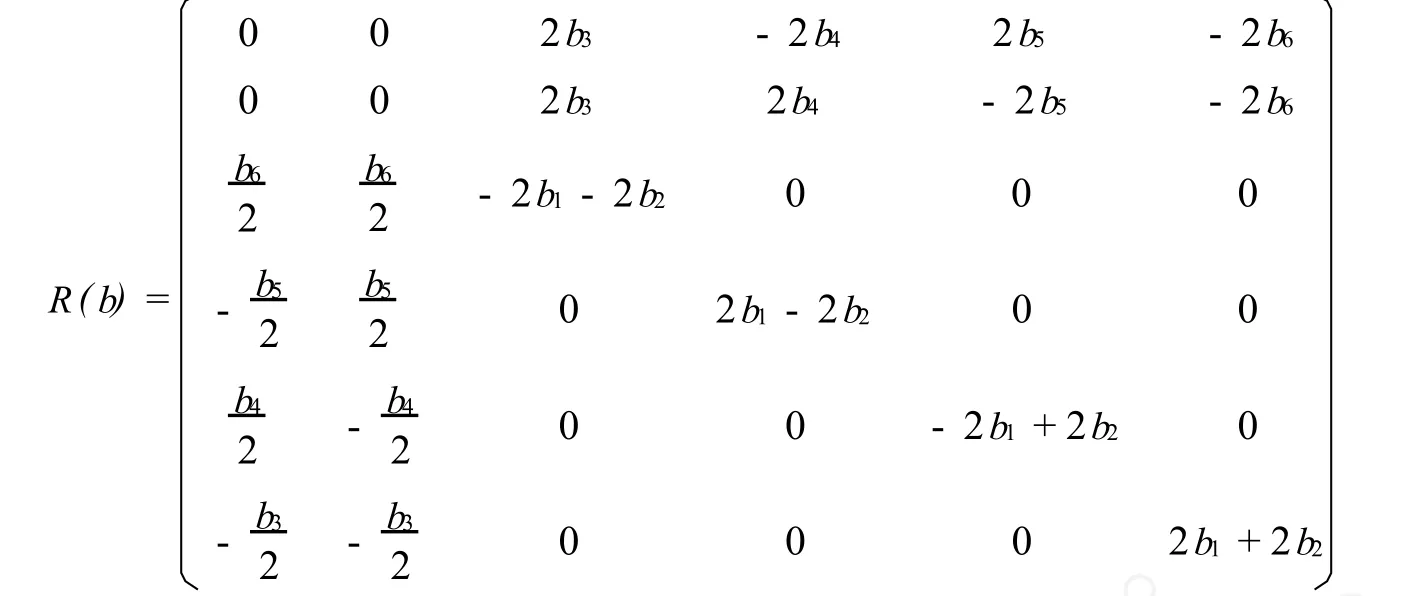
其滿足等式

如果取

易驗證方程(13)成立,即

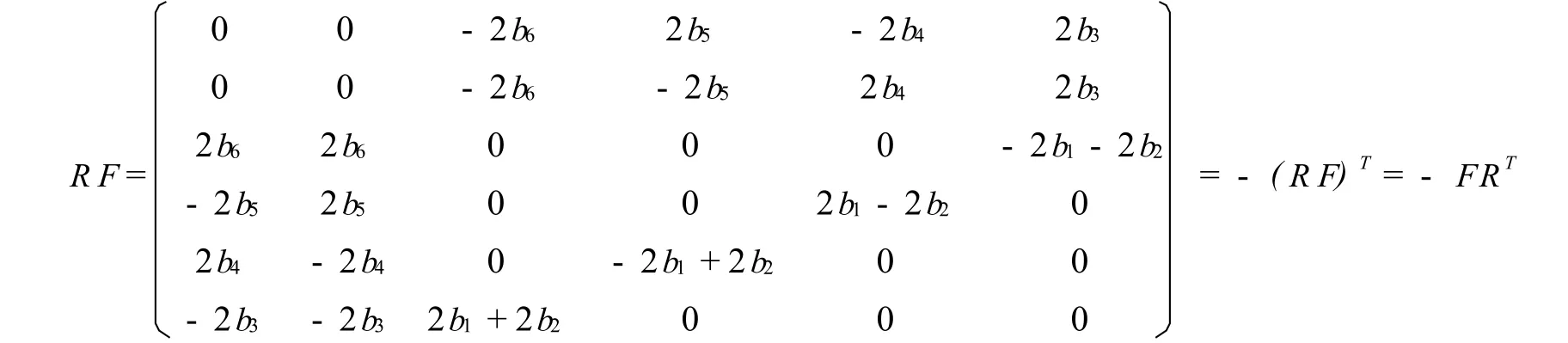
由(18)式我們可以得到下面的函數

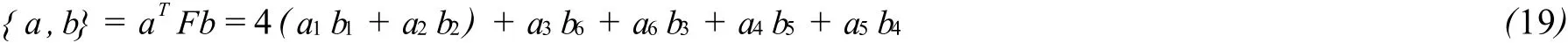
接下來,將利用李代數V6構造其Loop代數來得到兩類新的Liouville可積方程族,并利用屠格式和二次型恒等式得到其哈密頓結構。

例1 第一類可積方程族

考慮下面的Loop代數和其應用

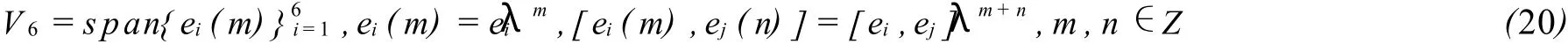
設

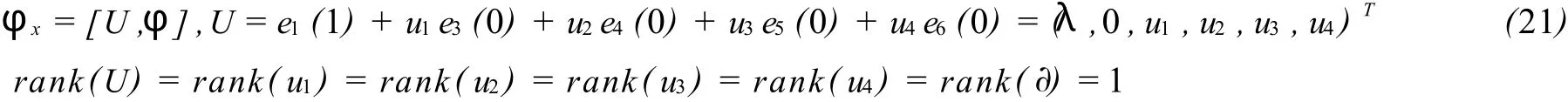
(21)和(22)式的相容性條件確定的靜態零曲率方程即

其中V的解如下

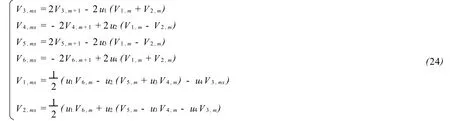
取

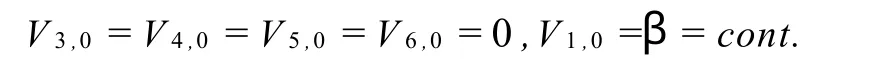
由(24)可得

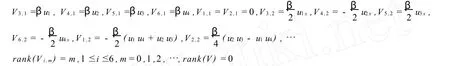
令

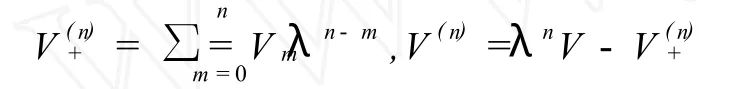
則方程(23)可分解為下面的形式

上式左端所含基元階數≥0,右端所含基元階數≤0。因此,我們可以得到

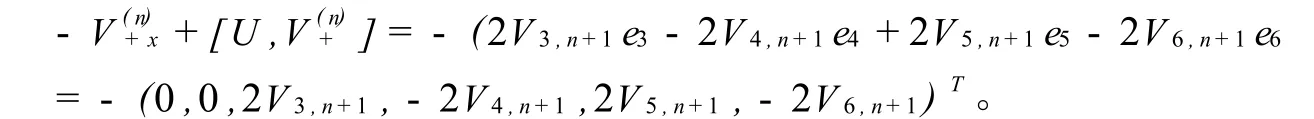
確定進化方程的Lax可積方程族

由(24)容易得到遞推關系

其中

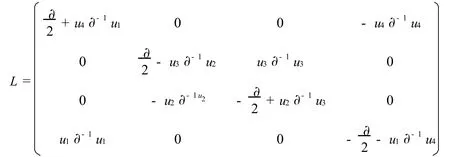
下面,推導(27)式的哈密頓結構。

記

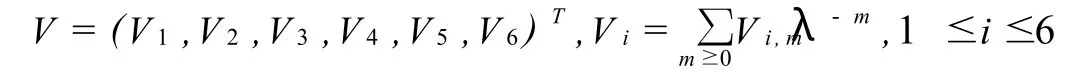
直接計算可得

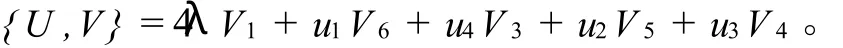
把上式代入二次型恒等式(16)可得

根據文獻[11]中求常數γ的方法,可以得到

比較(29)式中λ-n-2的系數可得

溝通交流是集體備課的核心，也是其區別于個人備課方式的最大特征.集體備課可以實現集中備課組所有老師的智慧與成果，實現取長補短，共同提高.在主要發言人對整節課的教學環節進行設計之后，備課組長就可以組織所有老師開展交流，對方案的不足進行補充，比如新課導入的方式、重難點的突破路徑、習題的設計與選擇等.

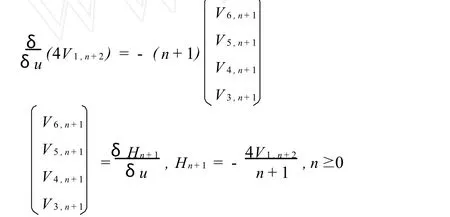
這樣,方程族(27)可寫成哈密頓結構

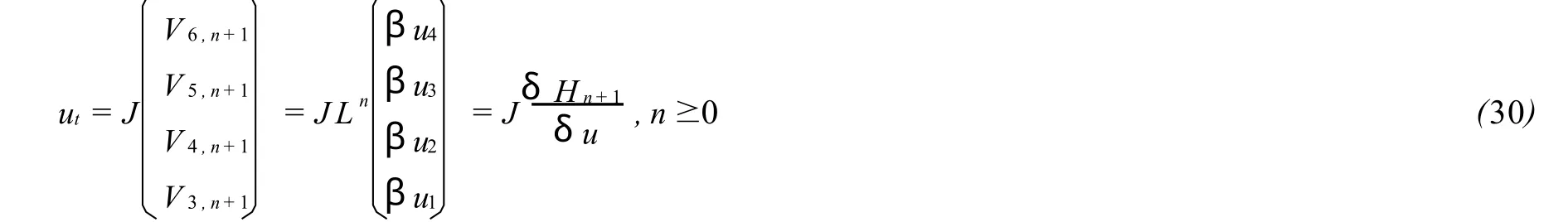
依照文獻[5],任一 Hk(k≥1)是(30)的守恒密度且任意的 Hm,Hm是兩兩對合的。經過復雜的計算可得 JL=L＊J。因此,方程族(30)是Liouville可積的。

例2 第二類可積方程族

在這一部分中我們將考慮如下不同于(21)和(22)中Lax等譜問題的U和V

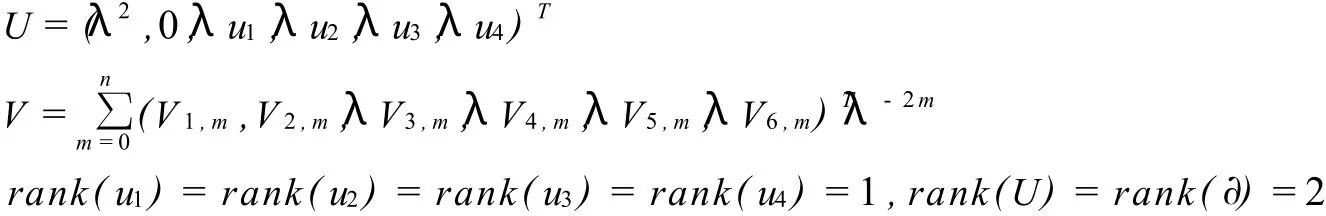
解方程

可得Vi,m的遞推關系

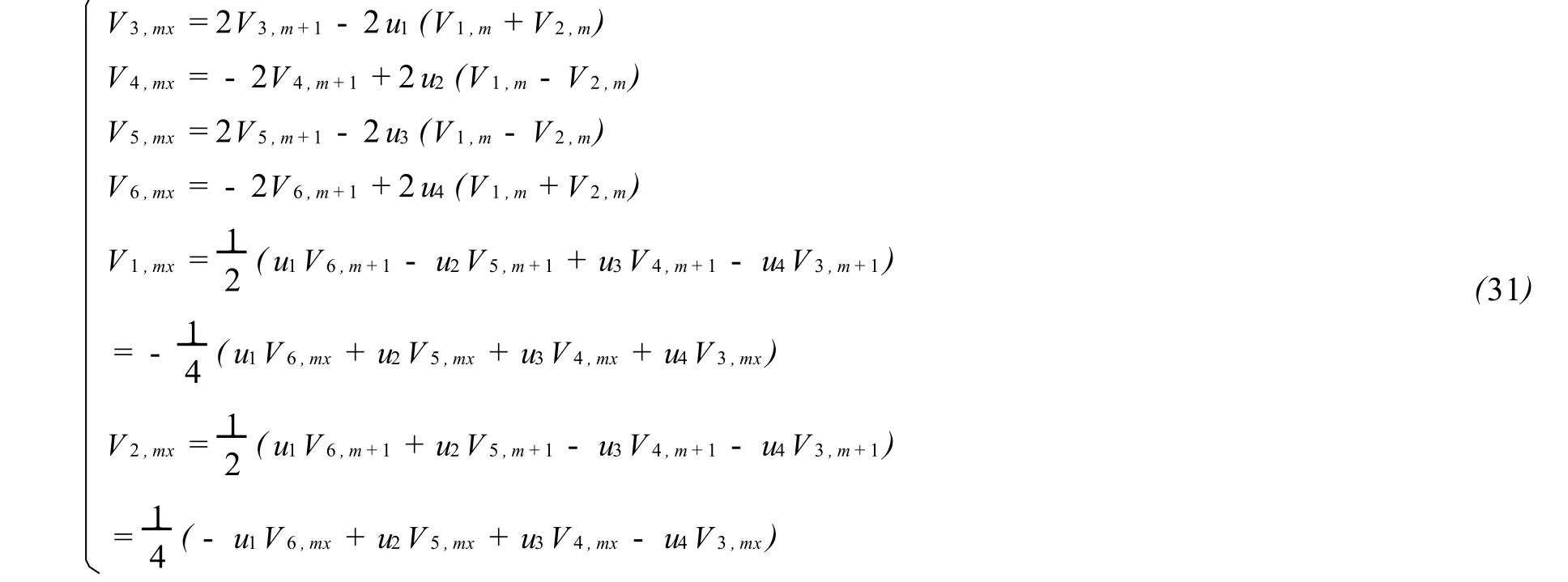
取

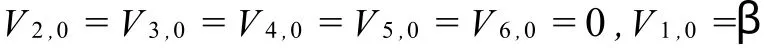
由(31)可得

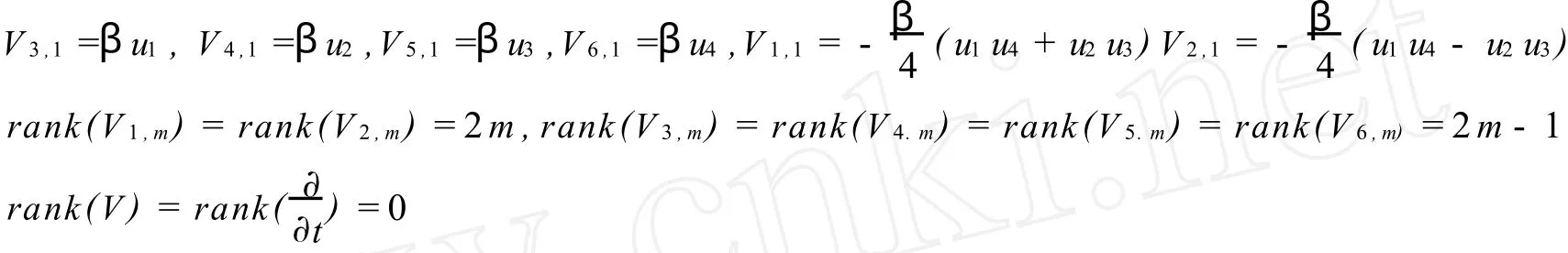
記

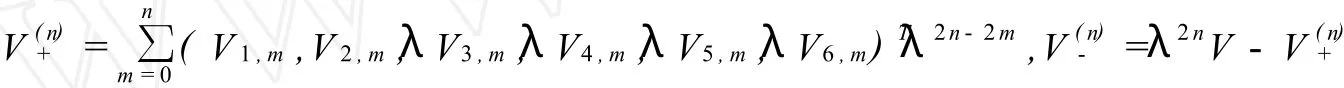
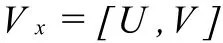
可寫成

上式左端所含基元階數 ≥0,右端所含基元階數≤1。因此,我們可以得到

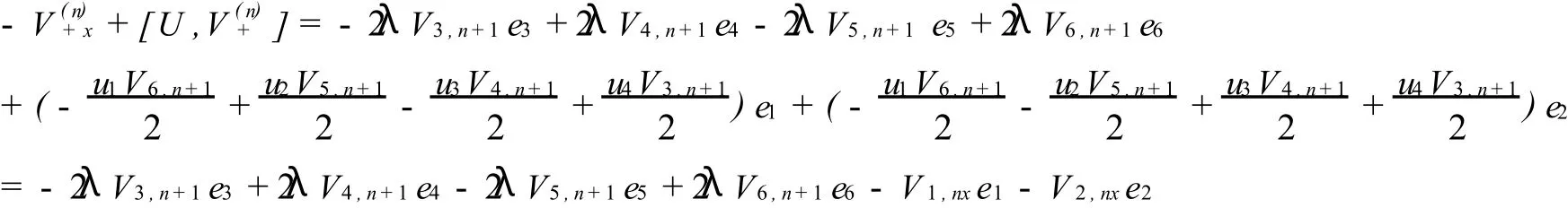
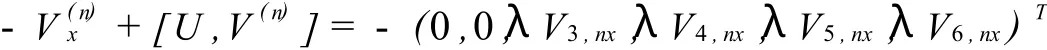
由零曲率方程

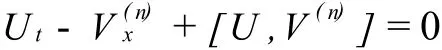
可得

由(31)式可得到下面的遞推關系

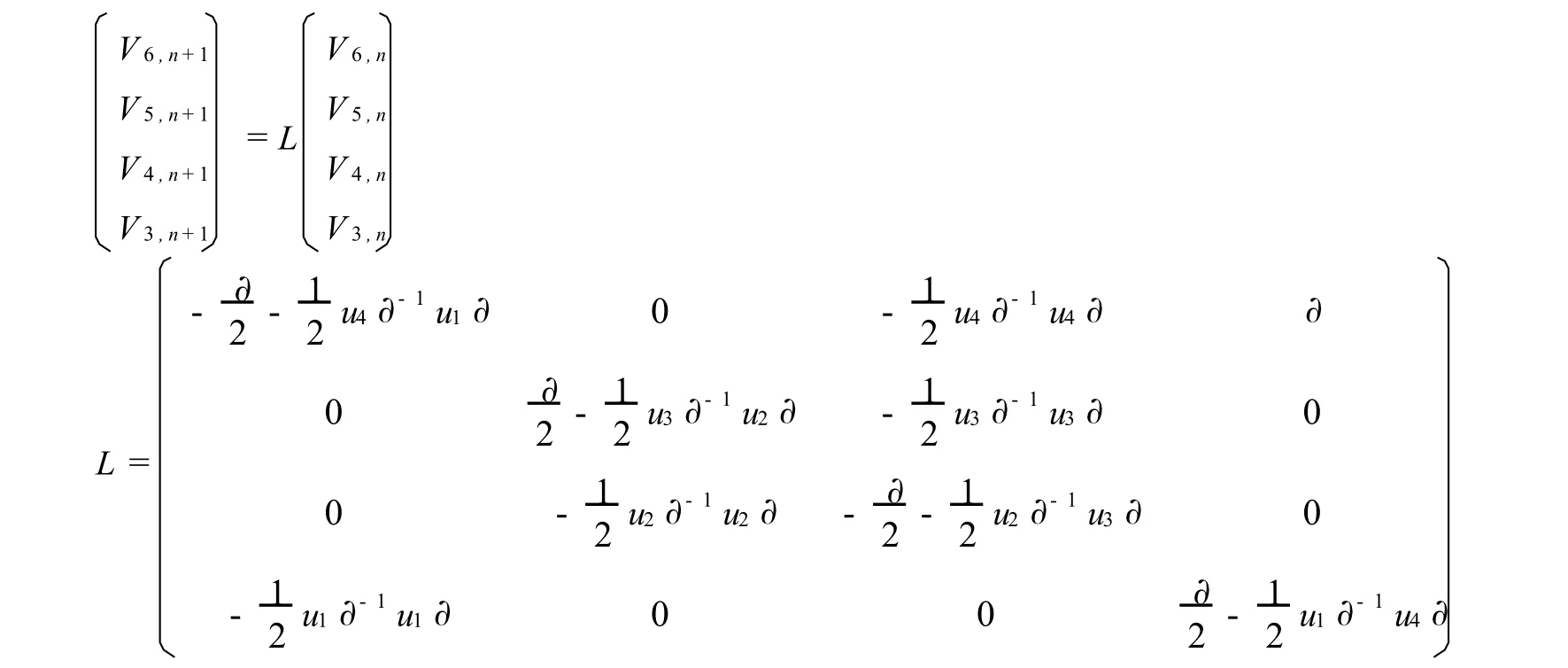
通過計算可得

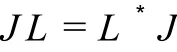
因此,Lax可積方程族(33)是Liouville可積的。

接下來利用二次型恒等式推導(33)式的的哈密頓結構。

記

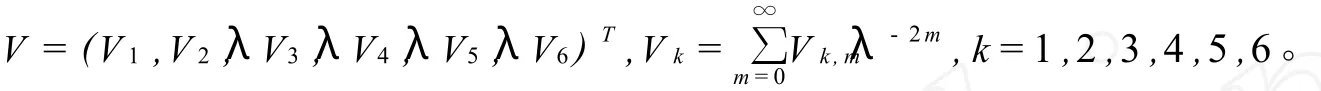
容易計算得

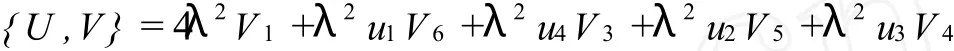
把上式代入二次型恒等式可得

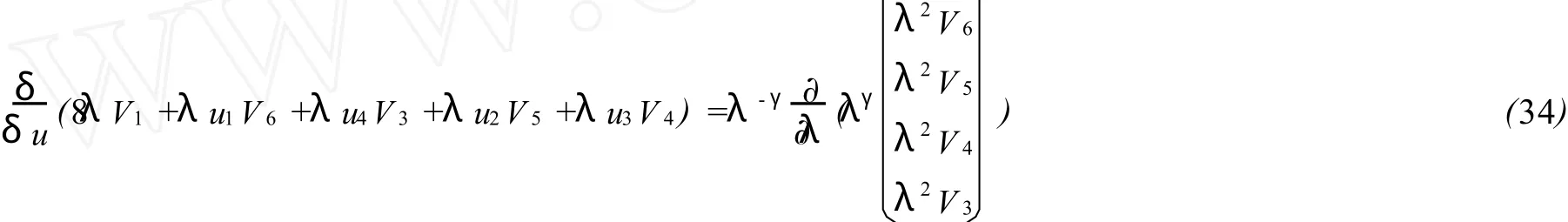
根據文獻[11]中求常數γ的方法,可得

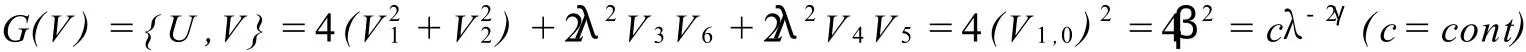
因此γ=0。

比較(34)式中λ-2n-1的系數可得

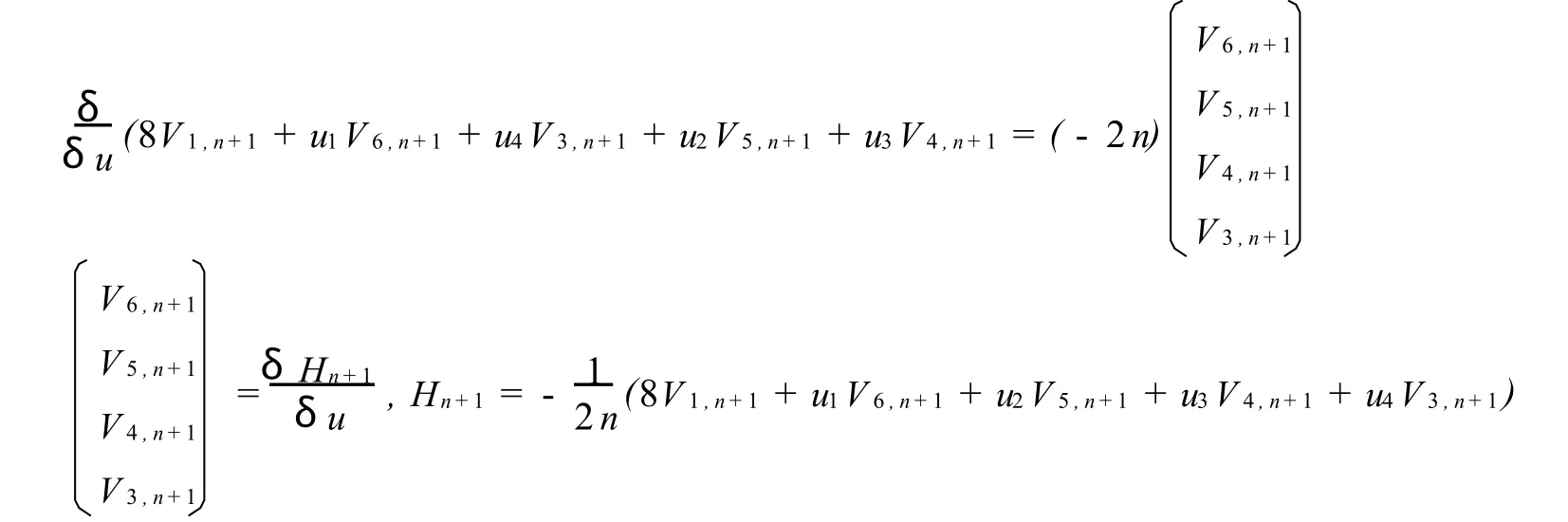
因此,方程族(33)可寫成下面哈密頓結構

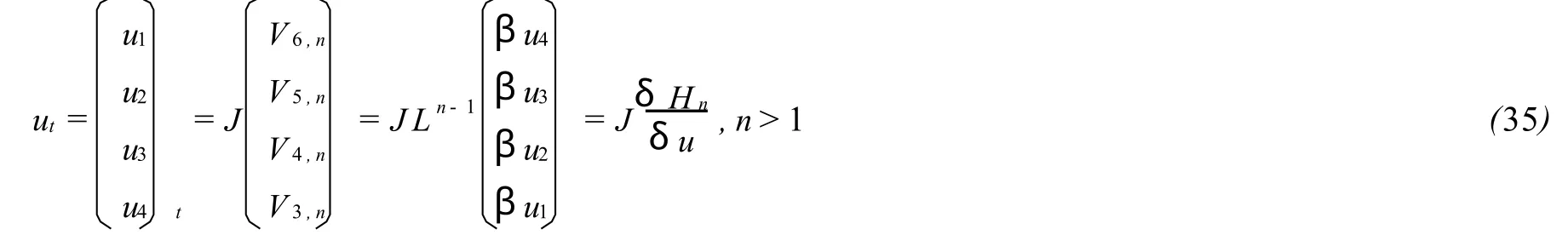
記 H1=-4V1,1,可得

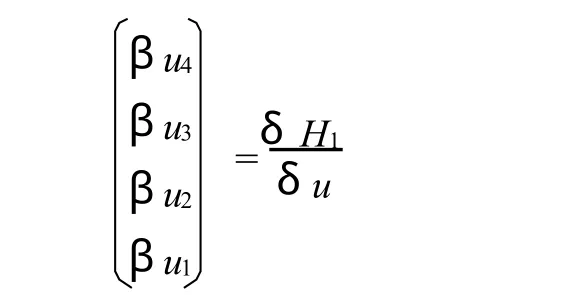
因此(35)式對于n≥1是成立的。

3 結論

本文介紹一類新的6維李代數并構造了兩類相應的Loop代數。作為其應用得到了兩類進化方程的可積方程族并利用二次型恒等式得到其哈密頓結構。利用本文的李代數還可以建立其他的Loop代數并利用本文的方法得到其他的新的可積系統。因此本文的方法有廣泛的應用。

[1]Newell A C.Solitons in mathematics and physics[M].Philadelphia:SIAM,1985.

[2]Ablow itz M J,Segur H.Solitons and inverse scattering transfo rm[M].Philadelphia;SIAM,1981.

[3]Wadati M,Konno K,Ichikawa Y H.A Generalization of inverse scattering method[J].J Phys Soc Jpn,1979,(46):1965.

[4]Wadati M,Konno K,Ichikawa Y H.New integrable nonlinear evolution equations[J].J Phys Soc Jpn,1979,(47):1698.

[5]Tu G Z.The trace identity,a powerful tool for constructing the Hamiltonian structure of integrable systems[J].J Math Phys,1989,30(2):330.

[6]Ma W X,Fuchssteiner B.Integrable coup lings of the hierarchies of evolution equations[J].Solitons and Fractals,2003, (16):263.

[7]Ma W X.Integrable coup lingsof soliton equations by perturbations I.A general theory and app lication to the KdV hierarchy[J].Methods and App lications of Analysis,2000,(7):21-56.

[8]Guo F K,Zhang Y F.A unified exp ressing model of the AKNSand its expanding integrablemodel[J].Chaos Solitons and Fractals,2004,19(5):1207.

[9]Guo F K,Zhang Y F.A type of expanding integrable model of the A KNS hierarchy[J].Acta Physica Sinica,2002(51): 951.

[10]Guo F K,Zhang Y F.The quadratic-form identity fo r constructing the Hamiltonian structure of integrable systems[J]. J Phys A,2005,(38):8537.

[11]Guo F K,Zhang Y F.Two unified fo rmulae[J].Phys Lett A,2007,366:403.