一種可變規格板材下料的優化方法

陳 奇，曹德列，饒運清

CHEN Qi, CAO De-lie, RAO Yun-qing

（華中科技大學 數字制造裝備與技術國家重點實驗室，武漢 430074）

0 引言

零件在一批大小和成本不同的板材上下料（可變規格板材下料）的問題普遍存在于板材加工類企業下料生產中。可變規格板材下料對板材規格不限定，可以是不同形狀、不同大小的矩形板材或者不規則板材，以及存在內部缺陷的非完整板材。由于需要統籌兼顧大小和成本不同的板材，可變規格板材下料相對于傳統同規格板材下料能獲得更為節省的下料方案。

可變規格板材下料注重于板材選擇和排樣布局的統籌最優，是一種組合優化問題，具有較高的復雜度。當前板材下料方面的研究多針對單張板材限定長寬或不限長度或者針對多張相同板材[1~4]，研究具體的排放算法而未能有效考慮不同規格板材的使用情況。Remesh Babu[5,6]等利用遺傳算法給出了多張不同板材時的排樣優化方法，然而目標函數只分析了材料面積未計入板材的使用數量，同時也沒有涉及到板材成本不同的情況。從可變大小二維裝箱問題的角度，Teodor Gabriel Crainic[7]利用箱子單位大小的成本進行分析，但是沒有優化箱子的序列選擇也沒有協調優化箱子之間的裝箱效果。

由于該類組合優化問題屬于NP-難問題，不存在多項式時間的算法，但遺傳算法在求解這類問題上效果突出。鑒于此，本文針對可變規格板材下料問題，以下料方案對應的成本最優為目標，利用遺傳算法優化板材序列和零件序列，并在解碼過程以模擬退火方式對排樣板材間零件加以優化調整提高板材總體利用率，得到最終下料方案。

1 問題分析

有m種大小和成本各異的板材B1，B2，…，Bm，每種 NB1，NB2，…，NBm張，每種成本為 C1，C2，…，Cm。板材的單位質量成本不完全相同。現需要將n個零件P1，P2，…，Pn全部排放在板材上，任一板材都能完全覆蓋任一零件，板材為所給板材中的一張或幾張，要求下料方案最優。

下料生產存在各種成本，和板材數量相關的有板材啟動成本、工人上下料作業成本等。傳統以最大化板材利用率為目標的研究具有一定局限性。板材選擇使用需要以合理方式權衡板材利用率和板材使用數量。本文以板材成本統一考慮板材利用率和使用數量。為增強對板材使用數量的控制，引進板材加工過程的中間成本。中間成本包括板材啟動成本和工人上下料作業成本。本文下料方案成本由板材成本和中間成本兩部分構成。

余料在下次下料時仍可使用，計算板材成本時相應扣除。余料成本利用原板材成本按余料面積占原板材面積百分比計算。設可用余料面積與板材面積比值為ηi，則余料成本為ηiCi。設中間成本相同，為Cs。數學模型為：

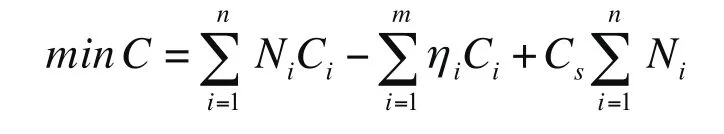
式中，Ni為板材Bi使用數量，Ni＜NBi。n為使用的板材種類，m為生成的余料數量。式中ηi和板材利用率相關，ηi越大利用率越高，所用板材相對越少，材料成本相對越低。

2 優化方法

可變規格板材下料一般流程如圖1所示，下料優化需要確定使用何種板材、每種板材的使用數量、每張板材上排放哪些零件、板材的使用順序以及零件的排放方式。零件序列按板材序列依次排樣，排樣結果為一張板材對應一組零件以及一種布局方式。排樣之后，每張板材排放哪些零件、零件的排放方式已知。板材使用種類和每種板材的使用數量受板材序列的影響，板材序列確定后二者相應確定。在既有排放算法基礎上，為進一步優化排樣效果，文章的關鍵任務是可變規格板材下料的板材序列優化、板材間排樣效果協調優化以及在此基礎上的總體優化處理。

圖1 下料流程圖

2.1 板材序列優化

板材選用是要從不同形狀、不同大小的矩形板材或者不規則板材以及存在內部缺陷的非完整板材中選擇合適的板材組合，并按最優順序使用。板材按序列依次使用，最佳的板材使用方案是一種板材序列的最佳組合方案。

下料優化是板材和零件的序列優化與布局優化。遺傳算法具有較強的全局搜索能力、魯棒性強，對于組合優化中的NP完全問題的求解非常有效。本文利用遺傳算法產生最佳板材序列，同時產生最佳零件序列。板材的利用率、使用數量等因素通過成本在目標函數中反映。

2.2 板材間排樣效果協調優化

零件序列按板材序列依次排樣，并通過向后搜索合適零件對可能存在的孔洞空域加以填充。排樣受零件面積的影響，排樣后期隨小型零件的減少，孔洞空域逐步增加。一張板材完全排滿后再排放下一張會使后續板材利用率逐漸降低。如果在當前限制某些后續搜索零件的插入，后續的排樣效果可以趨于更優。

排樣一般從板材左下角開始，排放過程會在板材右端和上端留下一些空域。如果在該零件組中增加或刪除一個零件重新排樣，排樣結果會發生較大變化。當增加一個或多個零件時，由于使用的零件不一樣，排樣布局效果發生改變，原空域部分可以得到填充，排樣結果可以趨于更優。

排樣結果為一張板材對應一組零件以及一種布局方式。優化以初始排樣結果為基礎展開，向著下料更優的方向進行，即增大余料提高利用率降低成本。協調優化是一個不斷調整排樣效果的過程。為增強優化調整得到解的可行性，調整方向以參與排樣的有效板材序列中某一張開始向后推動。

板材序列中參與排樣的板材為序列前Li張。取[1, Li-1]內隨機整數RB作為當前板材調整號，以RB號板材為基礎向后調整，RB號以前排樣情況不變。為避免產生多張余料，調整前RB及其后續所有板材連同對應零件重新排樣。調整時，RB號板材上無法再追加新零件，調整過程為減少其已有零件數量。同時為不破壞排樣過程帶來的擇優插入和避免調整結果惡化，每次調整量不宜過大，調整量取[0, a]內隨機整數RP。本文取a＝3，RP取RB板材對應零件組的后RP個。RB號板材及其調整后剩余零件重新排樣，RP個零件加入后續零件序列并在后續板材上重新排樣。

如果調整效果不優，以當前調整結果為基礎進一步調整存在更優的可能性，可以按概率接收作為新的基礎解。但當調整數量過多時以該結果為基礎無論怎樣調整，效率都低，此時接收概率降低。模擬退火隨著溫度降低，接收概率逐漸減小，最后系統收斂于某一能量最小的狀態，該狀態即可作為目標函數的全局優化值。解碼過程按模擬退火技術進行排樣再優化，步驟如下：

第一步：設置初始溫度；

第二步：設置循環計數器起點；

第三步：獲得[1, Li-1]內隨機整數RB，作為零件調整基礎板材序號，并就RB及后續板材連同對應零件重新排樣；

第四步：獲得[0, a]內隨機數RP，作為基礎板材上零件調整個數，按調整策略進行排樣優化調整；

第五步：如果當前結果更優，接收該結果，否則按概率接收；

第六步：如果步數小于終止步數，增大步數，轉向第三步；

第七步：如果未達到冷卻狀態，繼續降溫，轉向第二步；否則，輸出結果。

板材間排樣效果協調優化不追求每張板材布局最大化，通過排樣零件在不同板材間的優化協調提高總體利用率，尋求總體的布局更優。

2.3 基于遺傳算法的下料優化處理

根據圖1及問題分析，下料問題需優化板材序列、零件序列以及板材間排樣效果。本文優化方法以遺傳算法為基礎，在遺傳算法處理過程，將板材序列優化和零件序列優化結合起來。遺傳算法采用目標函數作為適應度函數，解碼過程對初始排樣結果按2.2中的方法對初始排樣結果協調優化。算法流程如圖2所示。

圖2 算法流程圖

2.3.1 種群初始化

遺傳算法染色體包括兩段，一段為零件序列，一段為板材序列。為便于序列化操作，所有零件和板材均從1開始標號。

零件序列部分采用隨機初始方式，部分采用有序初始方式[8]。有序初始方式首先將零件按面積非增序排列，面積相等時按長度非增序排列，對序列中每個標號隨機賦予“+”“-”表示旋轉方向，生成帶符號的有序種群。

板材序列主要由板材隨機排序生成。其中，板材序列中的m個序列，每個序列前NBi項為一種板材Bi，其余項按剩下板材單位質量成本非降序排列。另外1個序列直接按板材單位質量成本非降序排序。

2.3.2 遺傳算子

1）選擇算子

遺傳算法采用輪盤賭選擇，根據每條染色體的適應度的比例來確定該個體的選擇概率。

2）交叉算子

零件序列和板材序列交叉操作均采用LOX交叉。LOX是一種改進的次序雜交，能盡可能多的保留基因間的相對位置。操作時，先從兩父代P1、P2中選擇交叉點，交換選中的基因子串；然后將原P1(P2)中與P2(P1)子串不同的基因依次填入P1(P2)中非子串基因位置構成后代。如圖3，在選擇交叉位置3、7后按操作步驟進行得到子代C1、C2。

圖3 LOX交叉

3）變異算子

零件序列變異過程包括序列順序變異和旋轉方向變異，前者采用逆序變異，后者采用均勻變異。板材序列變異操作采用逆序變異。逆序變異根據選中的兩個變異點，將變異區間內基因順序顛倒產生新個體。

排樣時不是每張板材都參與排樣，而是依板材序列排樣直至零件全部排完。板材序列中只有序列前面一部分起實際作用。為提高板材序列交叉變異效果，交叉變異針對參與排樣板材序列部分展開。設板材序列中參與排樣的板材為序列前Li張。交叉操作時Li取兩序列較小者，并以此值作為變異位置基礎。交叉、變異過程兩位置之一的取值范圍限定在[1, Li]。

2.3.3 終止條件

按算法流程循環，直到下料方案滿足優化目標或達到預定的進化代數，停止計算，輸出結果。

3 算例驗證

算例以矩形排樣為例，排放算法采用文獻[8]中基于最低水平線的擇優插入算法。該方法在排樣過程按最低水平線法形成空洞時向后搜索合適零件插入當前序列位置并填入空洞。根據文章分析和算法框架，選用幾種大小和成本各異的板材以及相關零件進行實驗。板材材質為Q235，板厚20，不同規格之間單位質量成本不同。板材的大小、數量、成本等信息見表1。算例中設中間成本10，余料長度大于300時余料有效。

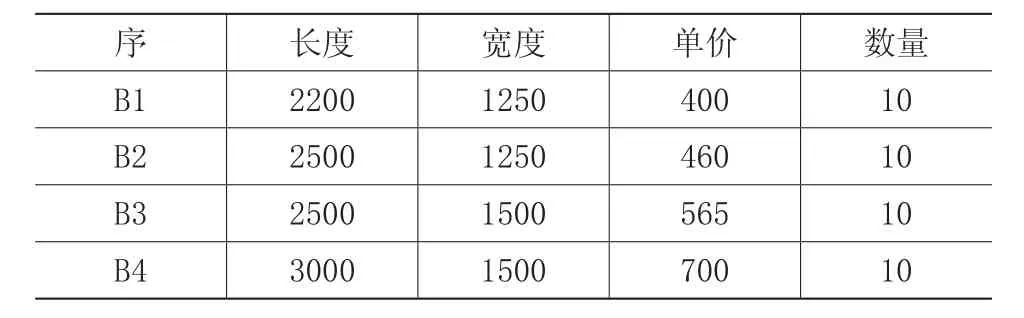
表1 板材信息

每種板材單獨排樣時所耗板材數量、利用率及成本如表2所示。

表2 同規格板材下料

表2中余料1是直接排樣后剩下的余料長度，余料2是進行排樣效果協調優化后剩下的余料長度。零件序列按板材序列依次排樣，余料出現在最后一張板材。其中B1、B4板材余料在排樣協調優化前后均小于300，視作廢料處理。成本按協調優化后使用情況計算。從表2可以看出，板材間排樣效果協調優化效果有效。

采用可變規格板材下料優化方法的結果如表3所示。

表3 可變規格板材下料

優化結果為板材B1使用3張、B2使用2張，順序為B2B1B1B2B1。其中B2無余料，最后一張B1板材余料長度941。總體優化成本為1998.9，較表2中同種規格板材下料成本更優。

單張板材利用率不高時，板材間排樣協調優化效果較為明顯。算例中所用矩形零件大小相差各異且較為明顯，同時數量不一。在算例中排樣效果再優化體現出其有效性。由表可以看出，本文方法能夠有效處理可變規格板材選用，并有效進行零件排樣效果再優化。

4 結論

本文針對可變規格板材下料優化問題，在板材的選擇使用過程中考慮板材利用率和使用數量兩因素，利用遺傳算法實現板材選用優化；在遺傳算法處理過程，將板材序列優化和零件序列優化結合起來，并在解碼過程以模擬退火方式對排樣板材間零件加以優化調整提高板材總體利用率。實驗表明，本文所論述的方法具有較強可行性，能夠有效降低下料成本。基于本文方法開發的優化模塊已嵌入到排樣軟件系統中，取得了良好的應用效果。利用本文提出的思路和方法，還可根據實際需求進一步研究在成本中考慮加工成本、庫存成本、延期交貨成本等因素的情況。

[1]陳學松,曹炬,方仍存.一種求解矩形件排樣問題的啟發式算法[J].鍛壓技術,2004,(05).

[2]陳仕軍,曹炬.矩形件優化排樣的一種啟發式算法[J].計算機工程與應用,2010,(12).

[3]張立馳,李健.基于遺傳算法的二維排樣問題求解新策略[J].南通職業大學學報,2009,(03).

[4]張麗平,李松.二維優化排樣方法及實現技術[J].計算機應用與軟件,2009,(04).

[5]A.Ramesh Babu, N.Ramesh Babu.Effective nesting of rectangular parts in multiple rectangular sheets using genetic and heuristic algorithms[J].Int J Prod Res, 1999,37(7)∶1625-1643.

[6]A.Ramesh Babu, N.Ramesh Babu.A generic approach for nesting of 2-D parts in 2-D sheets using genetic and heuristic algorithms[J].Computer-Aided Design, 2001,33(12)∶879-891.

[7]Teodor Gabriel Crainic, Guido Perboli, Walter Reiand.Efficient lower bounds and heuristics for the variable cost and size bin packing problem[J].Computers & Operations Research, 2011, 38(11)∶1474-1482.

[8]趙新芳,崔耀東,楊瑩等.矩形件帶排樣的一種遺傳算法[J].計算機輔助設計與圖形學學報,2008,(04).