旋轉折射光楔對控制模型在機載光電探測設備中的應用分析

時光煜，李明月，孫輝輝

(中航工業洛陽電光設備研究所，河南洛陽 471009)

旋轉折射光楔對控制模型在機載光電探測設備中的應用分析

時光煜，李明月，孫輝輝

(中航工業洛陽電光設備研究所，河南洛陽 471009)

在現代機載光電探測設備中，旋轉折射光楔對起著擴大探測視場和搜索范圍的重要作用。首先基于幾何光學和光的標量衍射理論對旋轉折射光楔對的折光特性進行了數學分析;然后結合其在機載光電探測設備中的功能要求，研究了一種旋轉光楔對控制模型，并基于該控制模型設計了旋轉折射光楔對的控制算法;最后，通過仿真實驗證明了該控制算法的正確性和可靠性。

機械光電探測設備;旋轉折射光楔對;控制模型;控制算法

0 引言

機載光電探測設備主要用于對空、對地探測，將飛機航線前方或左右景物形成圖像供平顯或多功能顯示器顯示，以增強飛行員對空地態勢的感知能力。為了擴大觀察范圍和實現對目標的快速搜索定位，要求機載光電探測設備具備方位掃描功能和在“上”、“下”、“左”、“右”、“中”5個探測方位之間實現快速切換的功能。旋轉折射光楔對(下文簡稱“光楔對”)是較常使用的光學元件，通過控制光楔對的旋轉，在光路中能起到偏折光線的作用。由于其具有控制靈活、機械運動平穩、振動噪聲小、掃描效率高，結構緊湊等優點，光楔對已被廣泛應用于性能先進的機載光電產品中［1］。

1 光楔理論概述

光楔就是頂角很小的折射棱鏡，在光路中能起偏折光線的作用，如圖1所示。

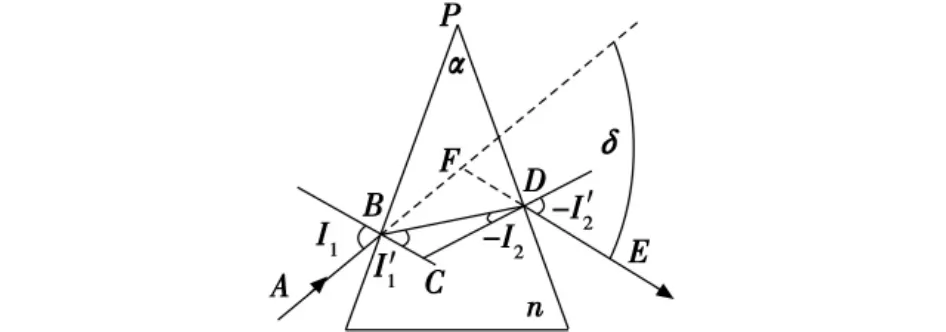
圖1 光楔對光線的偏折作用Fig．1The refractive property of light for dual-wedge prism system

光楔的工作面是兩個折射面，兩折射面的交線稱為折射棱，兩折射面間的二面角稱為折射棱鏡折射角，用α表示。垂直于折射棱的平面稱為主截面。由于沿折射棱方向的分量對光線的折射沒有貢獻，光線只在平行于主截面的方向發生折射［2］，為簡化討論，本文只討論光線在主截面內的折射情況。

在圖1中，光線AB沿主截面方向入射到折射棱鏡上，經兩折射面的折射，出射光線DE與入射光線AB的夾角δ稱為偏向角。設棱鏡折射率為n，光線在兩折射面上的入射角和折射角分別為I1、I1'和I2、I2'，可得入射角I1和偏向角δ之間的關系式［3－4］為

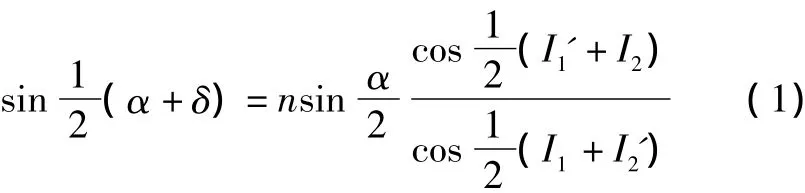
當I1為有限小時，由于α通常很小，可將式(1)簡化為

兩個相同的光楔一起使用，稱為光楔對。將其繞同一軸相對轉動，即一個光楔逆時針旋轉φ角，另一個光楔同時順時針旋轉φ角，折射光束就會在一定的范圍內變動，且有如下關系式［5－6］成立將式(3)整理后得:

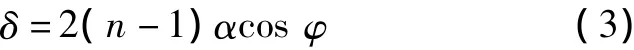
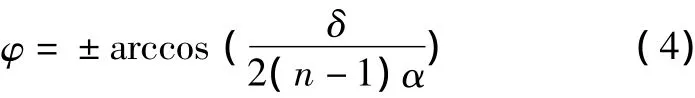
式(4)描述了光楔對產生的總偏向角δ與轉角φ之間的函數關系。

2 光楔對控制模型

在機載光電探測設備中，根據光楔對能對入射光線產生偏折作用的原理，通過控制光楔對的相對旋轉，可以實現對于光楔導向范圍內任意方向的探測功能。

在旋轉折射光楔對控制模型中，輸入量為機載光電設備的探測方位矢量(u，ξ)，其中u，ξ分別表示方位、俯仰角度;輸出量是光楔對的旋轉角度(φ0，φ1)，其中φ0，φ1表示光楔對的旋轉角度。

2．1 坐標系的建立

建立如圖2所示的“下左前”坐標系，即X軸方向垂直向下，Y軸方向水平向左，Z軸方向水平向前。設圖2中光楔對的主截面位于ZOX平面中，折射棱鏡折射角為α，折射棱為n，光楔對當前位置為初始零位。光線L2位于機載光電探測設備的外部，自右向左入射光楔對，出射光線L0平行于OZ軸向。

在圖2所示的坐標系中，光線矢量可以有兩種表示方法:1)使用光線的方位角和俯仰角(u，ξ)來表示，優點是物理意義清晰明確，便于終端用戶接受、操作; 2)使用光線與OZ軸向的夾角及其在XOY平面投影與OX軸夾角(δ，β)來表示，優點是便于建立數學模型，簡化數值運算。其中，δ為非負數，β從Z軸箭頭方向看進去逆時針為正。

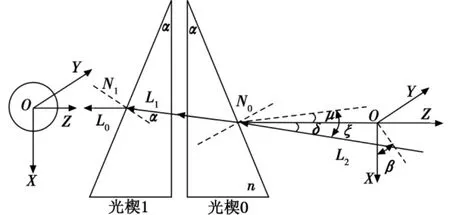
圖2 旋轉折射光楔對控制模型中坐標系的建立Fig．2The coordinate system of control model of dual-wedge prism

2．2 光楔對的旋轉角度計算

由于在建模過程中對于矢量光線的表示方法不同(控制模型輸入參數采用第1)種表示方法，而光楔對轉角的計算中使用第2)種表示方法)，因此，需要進行光線的矢量變換，以統一表示形式，方便數值運算。由圖2可知有如下函數關系式成立。

將式(5)整理后得

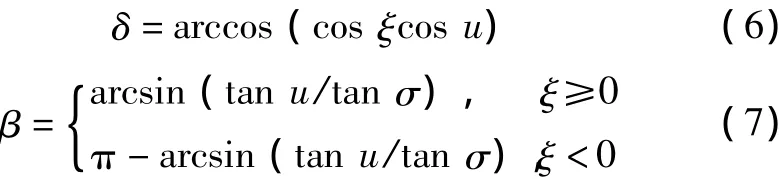
式(6)、式(7)描述了光線矢量從(u，ξ)到(δ，β)的轉換關系。

結合第1節的光楔理論知識，對于給定的輸入參量(δ，β)，可將待求解的光楔對的轉動角度(φ0，φ1)重寫為

其中:φ可由式(4)求得，不妨取正值，表示光楔對的相對轉角部分;β可由式(7)得到，表示光楔對的相同轉角部分。將φ、β代入式(8)可得:式(9)、式(10)描述了從光楔對控制模型中的輸入(u，ξ)到輸出(φ0，φ1)之間的函數映射關系。

2．3 約束方程

光楔對的光束導向范圍是一個關于旋轉軸對稱的圓錐立體角，即折射光線只能位于這個圓錐立體角之內，可用最大導向角δmax表示光楔對對于光線的導向能力。δmax的大小取決于光楔的折射角α和材料的折射率n，可表示為

3 光楔對控制算法

為了能夠對飛機的前方進行大范圍搜索，擴大探測范圍，要求機載光電探測設備具備掃描功能和對特定方位的快速觀察功能，將詳細討論實現上述功能的光楔對控制算法。

3．1 方位掃描控制算法

方位掃描控制算法首先根據當前機載光電設備的探測俯仰角度ξ和光楔對的導向范圍，確定掃描的水平軌跡;然后將掃描軌跡離散化，取出N個等步長的位置點，并計算出每個點處的方位矢量(u，ξ);緊接著根據式(6)、式(7)分別對這N個點進行矢量變換，即實現從(u，ξ)到(δ，β)的變換;接下來將(δ，β)代入到式(9)、式(10)中，求解出光楔對的轉動角度(φ0，φ1);最后發送指令給光楔對控制電機，控制光楔對旋轉到指定角度(φ0，φ1)。光楔對的方位掃描控制算法流程圖參見圖3。

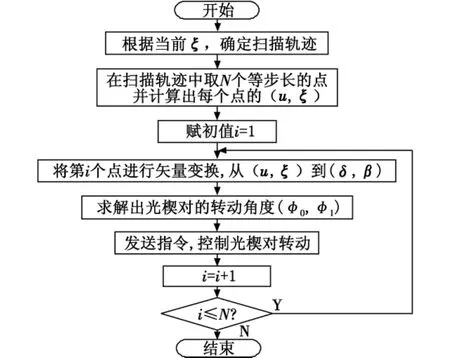
圖3 方位掃描控制算法流程圖Fig．3The flow chart of azimuth scanning algorithm

3．2 快速觀察控制算法

快速觀察算法就是在如圖4所示的“上”、“下”、“左”、“右”、“中”5個探測方位之間實現快速切換，滿足光楔對的旋轉角度盡量小的要求。另外，還希望兩個光楔的旋轉方向能夠盡量相反，以改善光楔對旋轉過程中視頻畫面的視覺效果。本文采用人工智能理論中狀態空間搜索的方法，從初始狀態節點出發，根據上述的規則約束，在狀態空間中搜索出一條解路徑，從而得出光楔對的最佳轉動角度［7－8］。

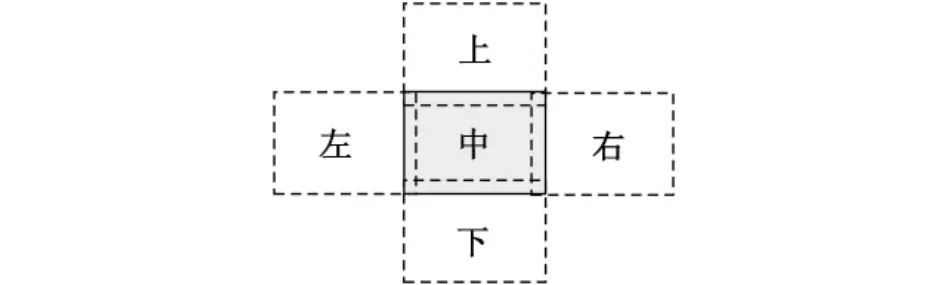
圖4 快速觀察示意圖Fig．4The sketch of quick watching

設光楔對的當前位置為P0(φ0，φ1)，目標位置為Pd(φd0，φd1)。光楔i(i=0，1)的當前位置φi可以重寫為

其中:ri為整數;θi∈［0，2π)。

為了滿足光楔轉動角度盡量小的要求，rdi取值空間為{ri－1，ri，ri+1}，相應φdi取值空間記為(φ1di，φ2di，φ3di)。這樣，目標位置的狀態空間便有9種不同的排列組合，分別記為Pijd(φid0，φjd1)(i，j=1，2，3)。

如果進行全狀態搜索，至少需要進行9次運算，運算量大，相應的運算時間較長。本文采用搜索深度為2級的有代價寬度優先搜索方法［9－10］，如圖5所示，僅需6次運算就可以找到最優解。

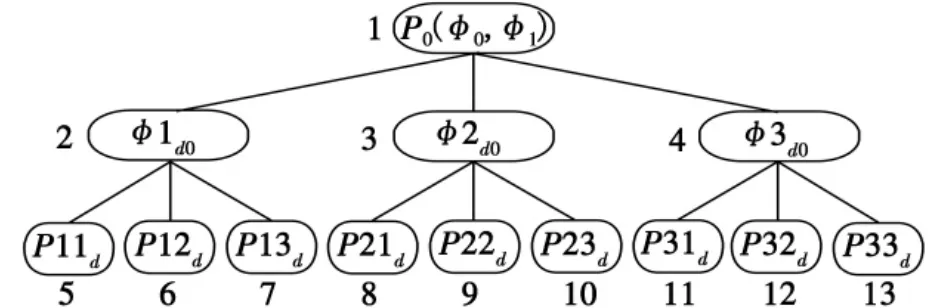
圖5 狀態空間搜索樹Fig．5A state space searching tree

在圖5中順次將每個節點編號，其中節點1表示光楔對初始角度(φ0，φ1)。第一級求解光楔0的轉動角度，定義式(9)為其代價函數;第二級求解光楔1的轉動角度，定義式(10)為其代價函數。建立Open表，用于記錄搜索過程中尚未考查的節點和新生成的節點，Open表的節點域可定義如下，示意圖見圖6。

圖6 Open表節點域定義示意Fig．6Node threshold of OPEN table

其中:j表示當前節點編號;i表示父節點編號;gj表示節點j的代價函數值;Sj表示節點狀態，取值空間為(0，1)，1表示該節點被選用，0表示未被選用。

狀態空間搜索算法如下:

1)初始化Open表，把初始節點(編號1)放入Open表中，且令g1=φ0，S1=1;

2)將Open表的第一個節點移出，并依據圖5所示的搜索樹擴展子節點2、3、4，依次放入Open表中;

3)依次將節點2、3、4從Open表中移出，計算函數值gj(j=2，3，4)，選取|g1－gj|最小的節點將其狀態標識Sj置1，設該節點為m，其余節點的Sj清零;

4)將節點m擴展子節點，并將新擴展的子節點依次放入Open表中;

5)依次從Open表中移出節點，計算函數值gj，選取|gm－gj|值最小的兩個進行比較，如果差別小于某特定值(例如小于10°)，則選取滿足(gj－φ1) (gm·g1)＜0的節點，否則選取|gm－gj|值最小的節點，設選中的節點為n，令Sn=1，其余節點的Sj清零;

6)將狀態標識Sj=1(j=1，2，…，13)的節點從搜索樹中順次找出，即成功找到了解路徑。

4 數值仿真及其分析

仿真實驗中選取光楔材料的折射率n=3．42，光楔頂角α=5．2°。由約束方程(13)可得最大導向角δmax=25．1680°。

首先，對光楔對的方位掃描控制算法進行Matlab數值仿真，分別選取俯仰角ξ為±11．46°(約合±0．2 rad)，方位角在導向范圍內往返掃描，掃描步長len設為2°(約合0．0349 rad)，掃描起始方位角位置為u= 0、方向為負。仿真結果參見圖7、圖8，圖中星號表示光楔0的轉角φ0，菱形表示光楔1的轉角φ1，實線表示方位角度u。實驗結果證明光楔運動平滑連續，控制效果良好。

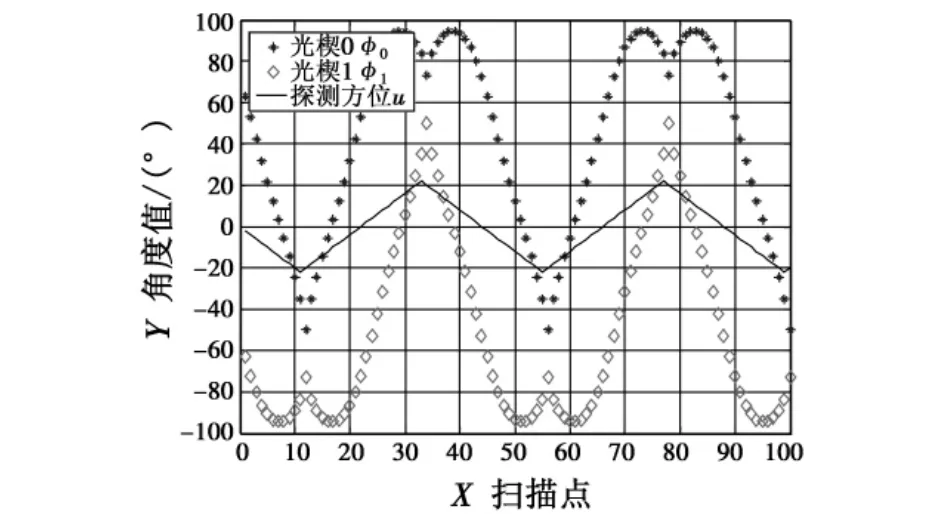
圖7 光楔對掃描仿真圖(俯仰角為11．46°)Fig．7The simulation diagram of dual-wedge prism system with pitch angle as 11．46°

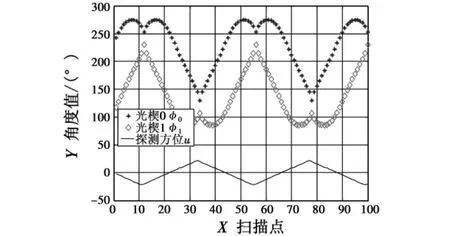
圖8 光楔對掃描仿真圖(俯仰角為－11．46°)Fig．8The simulation diagram of dual-wedge prism system with pitch angle as－11．46°

然后，將光楔對快速觀察控制算法進行仿真。在仿真實驗中，設“上”、“下”、“左”、“右”、“中”5個快速觀察位置的坐標(u，ξ)分別為(0，－18°)、(0，18°)、(21°，0)、(－21°，0)、(0，0)，快速觀察位置的切換次序為“中—上—下—左—右—中”，使用光楔對的快速觀察控制算法，在狀態空間中搜索出相應的解路徑，仿真結果參見表1。

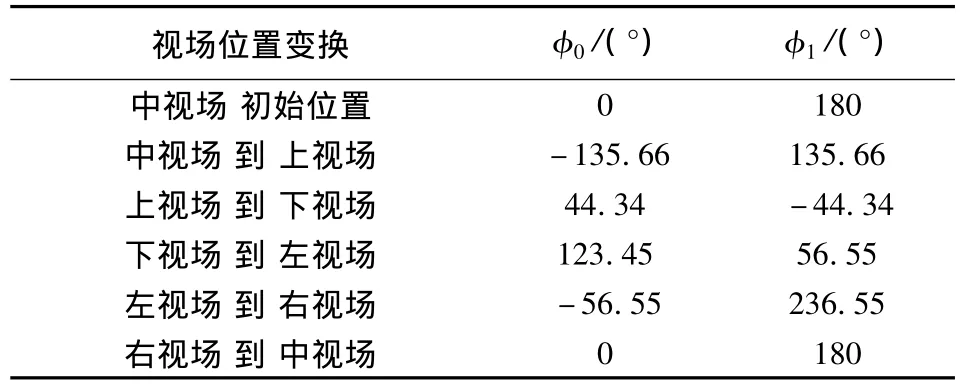
表1 快速觀察控制算法得到的解路徑Table 1The result of the quick watching algorithm

由表1所示的仿真結果可知，在各種快速觀察位置的切換過程中，控制效果符合預期的要求。

5 結論

文章首先基于幾何光學和光的標量衍射理論對旋轉折射光楔對的折光特性進行了數學分析，然后結合其在機載光電探測設備中的功能要求，研究了一種旋轉光楔對控制模型，并基于該控制模型設計了旋轉折射光楔對的控制算法。最后，通過仿真實驗證明了該控制算法是正確、有效的。

［1］郁道銀，談恒英．工程光學［M］．北京:機械工業出版社，2006．

［2］賀磊，袁家虎，李展，等．雙光楔高精度角度發生器設計［J］．光電工程，2002，29(6):46-49．

［3］玻恩M，沃耳夫E．光學原理［M］．北京:科學出版社，1978．

［4］徐斌．雙光楔實現外腔半導體激光器波長精密調諧研究［J］．激光與紅外，2008，38(5):444-446．

［5］韋中超，熊言威，莫瑋，等．旋轉雙光楔折射特性與二維掃描軌跡的分析［J］．應用光學，2009，30(6):939-943．

［6］楊輝．光測設備引導數據的誤差分析［J］．電光與控制，2010，17(7):83-86．

［7］王萬森．人工智能原理及其應用［M］．北京:電子工業出版社，2007．

［8］冷勁夫．單源路徑搜索算法的實現及比較［J］．地理空間信息，2010(3):154-156．

［9］馬蓉平．搜索推理技術與寬度優先搜索的實現［J］．赤峰學院學報:自然科學版，2009，25(3):42-43．

［10］陸釗．基于狀態空間表示的邏輯問題及其寬度優先搜索算法實現［J］．中國科教創新導刊，2007(467): 82-83．

Application of a Rotary Dual-Wedge Prism System Control Model in Airborne Photoelectronic Equipment

SHI Guangyu，LI Mingyue，SUN Huihui
(Luoyang Institute of Electro-Optical Equipment，AVIC，Luoyang 471009，China)

In airborne photoelectronic detection equipment，rotary dual-wedge prism system plays an important role for enlarging the detection scope and searching range．First，the refractive property of the dual-wedge prism system was analyzed according to the theories of geometrical optics and scalar diffraction．Then，a control model was established for the dual-wedge prism system considering the functional requirements of it in airborne photoelectronic equipment，and the control algorithms were given based on the model．The correctness and reliability of the control model and control algorithms were proved through simulation．

airborne photoelectric detection equipment;rotary dual-wedge prism;control model;control algorithm

V271．4

A

1671－637X(2011)12－0052－04

2010－12－03

2011－03－02

時光煜(1984—)，男，河南輝縣人，碩士生，研究方向為控制理論與控制工程。