如何解決“繩”和“彈簧”的突變類問題

張強

(奎屯市第一高級中學 新疆 奎屯 833200)

在中學物理中“繩”和“彈簧”都是一種理想化的物理模型.以輕質“繩”和輕“彈簧”為載體，設置復雜的物理情境，考查力的概念、物體的平衡、牛頓定律的應用及能的轉化與守恒，是歷年來高考命題的重點，幾乎每年高考試題均有所見.因此在高考復習中也引起了教師和學生的足夠重視．

大多數學生對此類問題涉及的知識要點不能深化理解，思維不夠靈活而導致容易出錯．而一些缺少經驗的教師通常又講不透徹涉及的知識要點，無法引導學生用創新思維去靈活運用解決這類問題．下面筆者通過多年積累的一些經驗，談談如何引導學生解決“繩”和“彈簧”的突變類問題．

首先要掌握“繩”和“彈簧”具有的基本特性.在中學物理中涉及到的“繩”和“彈簧”都是一種理想化的物理模型，都是輕質“繩”和輕“彈簧”，不計質量或者說質量和重力均可視為零.除此以外各自具有以下基本特性.

(1)對于“繩”來說，同一根繩的兩端及其中間各點的張力大小相等，繩只能受拉力，不能承受壓力(因繩能變彎曲)；繩對物體拉力的方向總是沿著繩指向繩收縮的方向，無論繩所受拉力多大，繩子的長度認為不變，即不考慮或忽略繩子的形變；若突然燒斷(或剪斷)繩的瞬間，繩子的拉力立即消失，即繩子中的張力可以突變．

(2)對于“彈簧”來說，同一彈簧的兩端及其中間各點的彈力大小相等，彈簧既能承受拉力，也能承受壓力(沿著彈簧的軸線)；由于彈簧受力時，發生形變需要一段時間，形變恢復也需要一段時間，在瞬間內形變量可以忽略；因此，在分析瞬時變化時，可以認為彈力大小不變，即彈簧的彈力不發生突變．

其次要靈活應用力與加速度的瞬時對應關系.由牛頓第二定律知，加速度是由合外力決定的，即有什么樣的合外力就有什么樣的加速度相對應．當合外力恒定時，加速度也恒定；合外力隨時間變化時，加速度也隨時間改變，且瞬時力決定瞬時加速度．可見，確定瞬時加速度的關鍵是正確確定瞬時作用力.因此“繩”和“彈簧”具有的基本特性的最后一點就是解決這類突變問題的關鍵．

下面通過幾道由淺入深的例題來詳細分析和討論如何解決“繩”和“彈簧”的突變類問題．

【例題1】天花板上用細繩吊起一個質量為m的小球,小球保持靜止，如圖1(a)．當突然燒斷(或剪斷)細繩的瞬間，下面小球的加速度為多大？

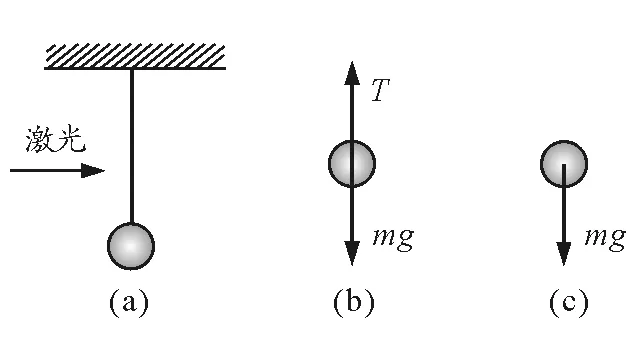
圖1

解析：以小球為研究對象，做燒斷(或剪斷)前和燒斷(或剪斷)時的受力分析.

剪斷前小球保持靜止，小球受兩個力，拉力T、重力mg，如圖1(b).有

T-mg= 0

剪斷細繩的瞬間，繩子的拉力立即消失，小球只受一個力，重力mg，如圖1(c)，有

mg=ma

解得a=g， 方向豎直向下.

【例題2】同時用細繩和輕質彈簧掛起一個質量為m的小球,小球保持靜止，如圖2(a)．當突然燒斷(或剪斷)細繩的瞬間，下面小球的加速度為多大？

解析：以小球為研究對象，做細繩燒斷(或剪斷)前和細繩燒斷(或剪斷)時的受力分析.

剪斷前小球保持靜止，小球受兩個力，彈力F彈、重力mg，如受力圖2(b).有

F彈-mg=0a=0

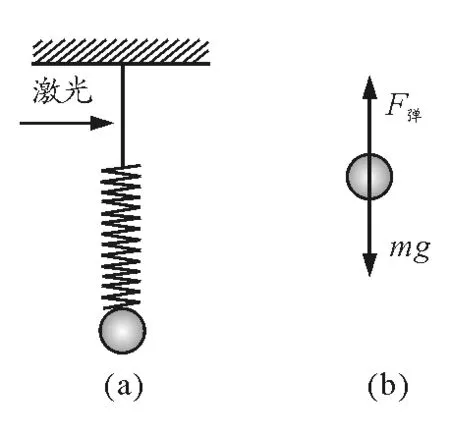
圖2

剪斷細繩的瞬間，繩子的拉力立即消失，但彈簧彈力大小不變，即彈簧的彈力不突變，小球仍受兩個力，彈力F彈和重力mg，如圖2(b).有

F彈-mg=0a=0

小球的瞬時加速度仍然為零.

【例題3】用輕質彈簧掛起一個質量為m的小球,小球保持靜止，如圖3(a).現用一束激光射向輕質彈簧，在燒斷輕質彈簧的瞬間，下面小球的加速度為多大？

解析：以小球為研究對象，輕質彈簧突斷前和輕質彈簧突斷時的受力情況一樣，如圖3(b).

彈簧突斷前

F彈-mg=0a=0

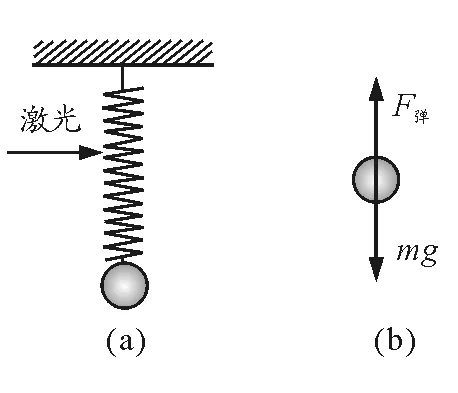
圖3

由于同一彈簧的兩端及其中間各點的彈力大小相等，彈簧突斷時，兩段彈簧的形變量都未來得及改變，彈簧彈力大小不變，即彈簧的彈力不突變，小球仍然滿足

F彈-mg=0a=0

小球的瞬時加速度仍然為零.

對于用激光打彈簧或彈簧突斷的問題，大多數學生包括教師都會產生疑慮：彈簧突斷前整根彈簧對物體的彈力和彈簧突斷瞬間下半段彈簧對物體的彈力能相等嗎？彈簧突斷瞬間畢竟變成兩根不同的彈簧，彈簧的勁度系數發生改變，兩根彈簧的形變量也不同，彈簧突斷的瞬間下半段彈簧對物體的彈力還等于物體的重力嗎？這個結論讓學生一時無法接受.如果學生能接受和理解，這類彈簧突斷的問題就非常簡單了，甚至題目一出答案直接就看出來．那么如何在教學中 突破這個問題？下面筆者介紹一種創新性思維方法來突破這個問題．

方法：用打斷后的兩段彈簧通過輕繩串聯等效替代即將打斷的原彈簧(圖4).用激光打斷彈簧就相當于直接打斷中間的輕繩．在打斷前，兩段彈簧的彈力相等都等于小球的重力.當打斷輕繩的瞬間，繩子的拉力立即消失，但彈簧B對小球的彈力大小不變，彈簧的彈力不突變，小球仍受兩個平衡力.有

F彈-mg= 0a=0

小球的瞬時加速度為零.

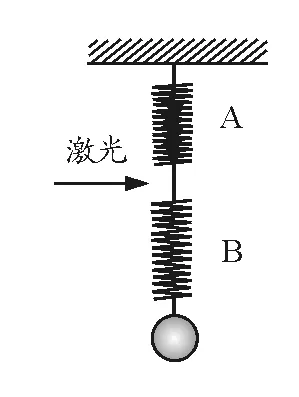
圖4

今后再遇到彈簧突斷的問題，就可以事先用打斷后的兩段彈簧通過輕繩的串聯來等效替代即將打斷的原彈簧，彈簧突斷的問題就轉化成了連接下半段彈簧的輕繩突斷的問題，這個問題就又回到了例題2．用這種創新性思維的方法來突破這個問題使復雜的問題變得淺顯易懂，學生也容易接受，更具有說服力．

【例題4】如圖5(a)，天花板上用細繩連接A球后懸于O點，A、B兩球由一輕彈簧相連保持靜止，A、B兩球質量都為m.如果將細繩燒斷，則在繩斷瞬間，兩球的加速度分別為多大？如果將彈簧燒斷瞬間，兩球的加速度又分別為多大？

解析：以A、B兩球分別為研究對象，做燒斷前和燒斷時的受力分析．

燒斷前A、B靜止，如圖5(a);A球受三個力，拉力T、重力mg和彈力F彈，如圖5(b)；B球受兩個力，重力mg和F彈′，如圖5(c)，取向上的方向為正.

A球T-mg-F彈=0

(1)

B球F彈′-mg=0

(2)

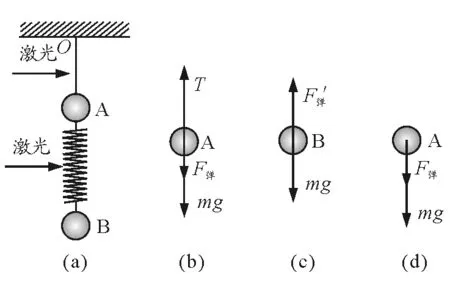
圖5

由式(1)、(2)解得

T=2mgF彈=F彈′=mg

(1)將細繩燒斷時，A球受兩個力，因為繩的拉力T立即消失，而彈簧有形變，瞬間形變不改變，彈力還存在．如圖5(d)，A球受重力mg、彈簧給的彈力F彈．同理，B球受重力mg和彈力F彈′．

A球 -mg-F彈=maA

(3)

B球F彈′-mg=maB

(4)

由式(3)解得aA=-2g(方向向下)

由式(4)解得aB=0

錯解：細繩燒斷時，以(A+B)為研究對象，系統只受重力，處于完全失重狀態，所以加速度為g，則A、B球的加速度為g．出現上述錯解的原因是研究對象的選擇不正確.由于細繩燒斷時，A球受力發生改變，B球受力不變，A、B球具有了不同的加速度，不能做為整體研究．

(2)將彈簧燒斷瞬間，彈簧有形變，瞬間形變不改變，彈簧彈力大小不變．因此彈簧燒斷瞬間A、B兩球受力情況不變．由圖5(b)，A球受三個力，拉力T、重力mg和彈力F彈；如圖5(c)，B球受兩個力，重力mg和F彈′．

A球T-mg-F彈=0

B球F彈′-mg=0

解得aA=0aB= 0

【例題5】如圖6(a)所示，一質量為m的物體系于長度分別為L1、L2的兩根細繩上，L1的一端懸掛在天花板上，與豎直方向夾角為θ，L2水平拉直，物體處于平衡狀態．

(1)現將細繩L2剪斷，求剪斷時物體的瞬時加速度多大.

(2)若將圖6(a)中的細繩L1改為長度相同、質量不計的輕彈簧，如圖6(b)所示,其他條件不變.求剪斷細繩L2時物體的瞬時加速度多大.

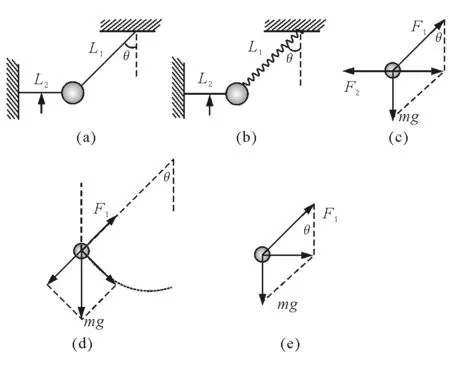
圖6

解析：(1)如圖6(a)，以質量為m的物體為研究對象，細繩L2剪斷前受力情況如圖6(c),物體受三個力,即細繩L1、L2的拉力分別為F1、F2和重力mg,物體處于平衡狀態，此時滿足

當細繩L2剪斷瞬間，繩L2的拉力F2突然消失，繩L1上張力的大小發生了突變，物體在細繩L1的拉力F1、重力mg的作用下將沿弧線下擺，如圖6(d).

此瞬間

F1=mgcosθ

F合=mgsinθ=ma

解得

a=gsinθ

(2)如圖6(b)，當細繩L2剪斷瞬間，繩L2的拉力F2突然消失，彈簧L1的形變量未來得及發生變化，彈力F1的大小和方向都不變，此時物體只受重力mg和彈力F1兩個力，如圖6(e)，物體所受的合力與F2等大反向.由牛頓第二定律得

F合=mgtanθ=ma

所以

a=gtanθ