高壓下β硼電輸運行為中的晶界效應

楊 潔，張冬梅

(1.空軍航空大學基礎部，吉林 長春130022；2.吉林大學 原子與分子物理研究所，吉林 長春 130012)

1 前言

多晶樣品的晶界不同于單晶，因為這些晶界可能在決定材料的物理性質方面起主要作用.因此，探究晶界如何顯著地影響材料的電輸運行為非常重要.單頻交流電阻測量方法可用于對單晶和純的流體樣品的研究，但對多晶或液體混合物樣品卻不適用.對后者而言，變頻交流阻抗譜方法在幾十年前就廣泛應用于分離晶粒內部和晶界對總阻抗的貢獻[1，2]，但是這種方法還未清晰地揭露出晶界在這些復雜樣品中起何種作用，對晶界貢獻的解釋仍有分歧.如Shankland等人[1]以及后來的Kariya等人[3]發現，對橄欖石而言，晶界為提高其電導率；相反，Schock等人[4]研究了高壓下的多晶橄欖石粉末，認為晶界電導率對樣品總的電導率有非常小的影響.此外，Haak[5]認為在560℃到1150℃范圍內，多晶橄欖石的電導率比單晶高；并且，單晶和多晶橄欖石樣品的電導率在1400℃左右會聚到一點，他認為此種現象可能歸因于離子傳播路徑的增加.可見，所有對橄欖石電學性質的研究已經表明，晶界對總電阻有貢獻，但此貢獻對總阻抗而言是正面亦或負面仍不確定.隨著變頻交流阻抗譜方法的發展，晶粒和晶界貢獻的分離已可通過測量它們的相對比率來實現[6-8].

在材料科學領域，硼及富硼化合物占有很重要的位置，因為富含硼的物質有很高的硬度[9]和高溫超導等現象[10].基于以上這些原因，硼成為最近幾十年實驗和理論研究的熱點.Werheit等人[11]認為硼樣品中的載流子為空穴，傳輸模式為跳躍傳導.Erements等人[12]通過實驗證明，β硼在幾個開爾文的溫度下將由半金屬變為超導體；而Papacnstantopoulos等人[13]則通過第一性原理計算發現了β硼的超導現象；趙等人[14]利用第一性原理研究了β硼的壓致金屬化.盡管對β硼的研究已有很多，但晶界對β硼電輸運性質的影響幾乎未被討論過.基于此，本文利用金剛石對頂砧變頻交流阻抗譜測量方法，進行了高壓下多晶β硼樣品的實驗研究，旨在揭露晶界在總阻抗中的作用及晶界處電輸運的傳導機制.β硼具有較大的斜方結構，每個晶胞里包含105個硼原子，二十面體位于斜面體的每一個頂角處和每一個邊的中心，中間的團簇沿對角線排列.

2 實驗

本工作采用Mao-Bell型DAC產生高壓，交流阻抗譜測量采用Solartron1260二終端頻響分析儀.電極的制備過程在以前的工作中有詳細的介紹[15].頻率范圍為10μHz～30MHz，交流電壓選用0.1V，測量過程中保持室內溫度穩定.實驗最高壓力為27.5GPa.

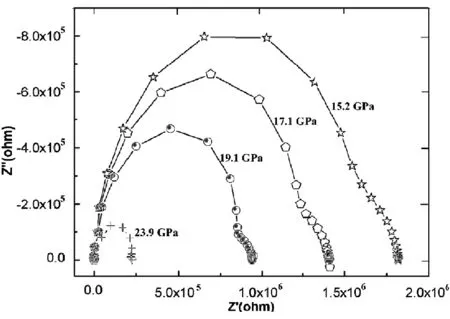
圖1 高壓下β硼的阻抗譜

3 實驗結果及分析

圖1展示的是不同壓力下β硼的交流阻抗譜，壓力點分別為15.2，17.1，19.1，23.9GPa，橫軸為阻抗實部，縱軸為阻抗虛部.圖譜左側為高頻部分.電阻值為曲線與橫軸的截距.最好的情況下，阻抗譜會展示出三部分分離的貢獻，高頻區為晶粒貢獻，中頻區為晶界貢獻，低頻區為電極貢獻[16].然而，本實驗只出現兩個半圓弧，分別對應著兩個傳導過程：左邊為晶粒傳導，右邊為晶界傳導[16]，而電極的貢獻沒有觀察到.

由圖1可以明顯的發現以下三點：(1)晶粒電阻和晶界電阻均隨壓力而減小，表明帶隙隨壓力而減小；(2)23.9GPa處的阻抗譜與其它三個壓力點明顯不同，對應著β硼電導率的顯著增加，可歸因于晶粒表面缺陷的變化；(3)23.9GPa處，晶界傳導幾乎消失.在23.9GPa阻抗譜獨特的模式依賴于粒子間的范德瓦爾斯力(FVDW).

依據Hamaker[17]的理論，FVDW不僅存在于單獨的原子或分子間，而且存在于粒子之間.Hamaker利用London推測的附加假定[18]，獲得了FVDW的數學表達式，對于距離H，由兩種不同物質1和2組成，半徑分別為R1和R2的兩個固體球形粒子，FVDW表示為：

FVDW=AR/6H2

(1)

其中，A=π2q1q2λ1，2，為Hamaker常數，R為半徑的幾何平均值，R=R1R2/2(R1+R2).在A的表達式中，q1和q2分別為兩種相互作用粒子的原子密度，λ1，2為London-范德瓦爾斯常數，其值依賴于原子數量.對于本實驗，A和R值均不改變，因此，FVDW只和H2的倒數成比例關系.

存在于兩種粒子間的范德瓦爾斯力屬短程作用力，當兩種粒子的間距足夠小時出現.在我們的模型中，β硼晶粒屬于此類粒子.隨著壓力的增加，晶粒間距逐漸減小，其表面懸鍵開始相互作用.隨著距離的減小，這種相互作用逐漸增強，當壓力達23.9GPa時導致范德瓦爾斯力和懸鍵相互作用的出現.這使得β硼晶界對載流子的散射減弱，導致23.9GPa時阻抗特性的異常變化.這一基本的物理圖象對β硼樣品是有效的，也可能適用于所有種類的多晶樣品，電阻變化的幅度可能依賴于晶粒表面缺陷、懸鍵的種類和數量甚至位錯的類型.

為深入分析晶界在電輸運性質中的作用，圖2給出了不同壓力下阻抗虛部隨頻率的變化關系，由此可得出弛豫頻率.虛部隨壓力迅速減小，表明晶界對β硼電輸運的貢獻減弱.弛豫頻率依賴于載流子狀態，壓力會使β硼載流子態發生不對稱，進而影響弛豫頻率.阻抗虛部隨頻率的變化表現為兩個相反的趨勢，大的趨勢表現為鐵核導性特征，小的頻率趨勢則表現為典型的容性特征[19].因此，β硼阻抗虛部主要為導性特征，同時伴隨著小的容性部分.

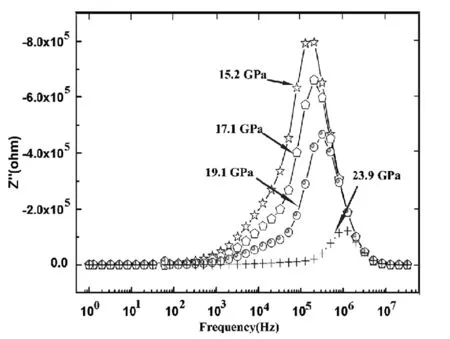
圖2 高壓下β硼阻抗虛部隨頻率的變化

利用Zview阻抗分析軟件對實驗數據進行擬合，可以得到晶粒電阻Rg和晶界電阻Rgb.設RT為總電阻，即RT=Rg+Rgb，則Rgb/RT隨壓力的變化(如圖3所示)反映了晶界電阻對總電阻的貢獻.

當壓力達23.9GPa時，圖3中的曲線出現微小的下降，此時晶界對總電阻的貢獻僅為7%.前面已經提到，在23.9GPa處，β硼晶界對電荷載流子的散射減弱，晶界對載流子的較小貢獻可解釋如下：晶界處存在許多缺陷能級，例如空位，糾纏態等局域態的電荷陷阱能級，它們將捕獲晶體內的電荷載流子.在純的β硼中空穴傳輸是主要的傳導機制，因此在其晶界處的陷阱能級將從近臨的晶粒處俘獲空穴載流子，從而導致晶粒內部空穴的消耗和晶粒邊界處載流子的積累.因此體電阻對總電阻的貢獻比晶界電阻大.

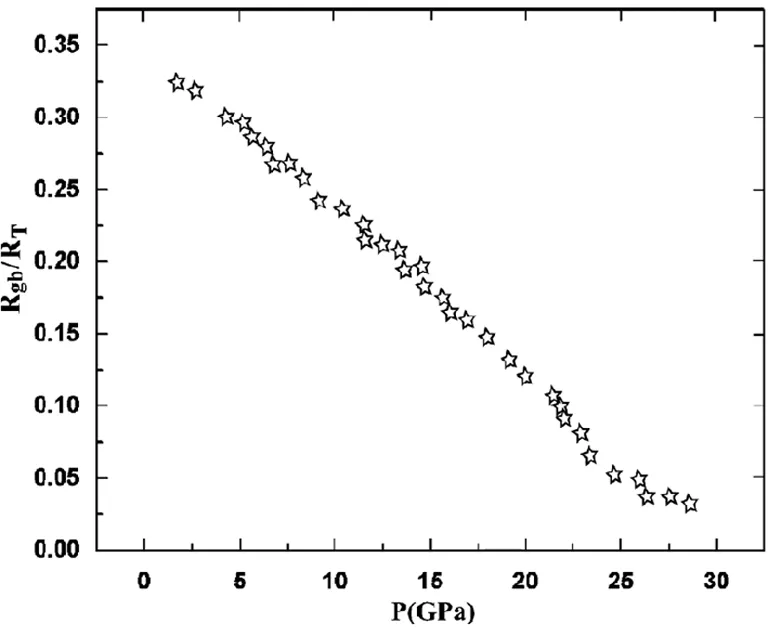
圖3 β硼中Rgb/RT隨壓力的變化關系

4 結論

本文利用交流阻抗譜測量方法，系統討論了高壓下晶界效應對β硼電輸運性質的影響，結果表明：晶粒電阻和晶界電阻均隨壓力逐漸減小，晶粒電阻對β硼總阻抗起主要作用；晶界電阻對總電阻的貢獻隨壓力逐漸減小，當壓力達23.9GPa時，隨著范德瓦爾斯力及晶界相互作用的出現，晶界傳導幾乎消失.

[1]T.J.ShanklandandH.S.Waff.Partialmeltingandelectricalconductivityanomaliesintheuppermantle[J].JournalofGeophysicalResearch.1977，82:5409-5417.

[2]J.FleigandJ.Maier.Microcontactimpedancemeasurementsofindividualhighlyconductivegrainboundaries:GeneralaspectsandapplicationtoAgCl[J].PhysicalChemistryChemicalPhysics，1999，1:3315-3320.

[3]K.A.KariyaandT.J.Shankland.Electricalconductivityofdrylowercrustalrocks[J].Geophysics，1983，48:52-61.

[4]R.N.Schock，A.G.Duba，H.C.Heard，andH.D.Stromberg.Theelectricalconductivityofpolycrystallineolivineandpyroxeneunderpressure[J].High-PressureResearch:ApplicationsinGeophysics，1977：39.

[5]V.Haak.inHigh-PressureResearchesinGeoscience[G]//W.Schreyer，editor.E.Schweizerbart'scheVerlagsbuchhandlung，Stuttgart，1982：407.

[6]J.E.Bauerle.Studyofsolidelectrolytepolaizatinbyacomplesadmittancemethod[J].JournalofPhysicsandChemistrofSolids，1969，30(12):2657-2670.

[7]E.LilleyandJ.E.Strutt.BulkandGrainBoundaryIonicConductivityinPolycrystalline''-Alumina[J].PhysicaStatusSolidiA，1979，54(2):639-650.

[8]M.J.Verkerk，B.J.Middelhuis，andA.J.Burggraaf.Effectofgrainboundaryesontheconductivityofhigh-purityZrO2-Y2O3ceramics[J].SolidStateIonics,1982，6(2):159-170.

[9]V.V.Brazhkin，A.G.Lyapin，andR.J.Hemley.Harderthandiamond:dreamsandreality[J].PhilosophicalMagazineA，2002，82(2):231-253.

[10]J.Nagamatsu，N.Nakagawa，T.Muranaka，Y.Zenitani，andJ.Akimitsu.Superconductivityat39Kinmagnesiumdiboride[J].Nature，2001，410:63-64.

[11]H.WerheitandH.G.Leis.OntheConductivityMechanismof-RhombohedralBoron[J].PhysicaStatusSolidiB，1970，41(1):247-253.

[12]M.I.Eremets，V.V.Struzhkin，H.K.Mao，andR.J.Hemley.SuperconductivityinBoron[J].Science，2001，293:272-274.

[13]D.A.PapaconstantopoulosandM.J.Mehl.First-principlesstudyofsuperconductivityinhigh-pressureboron[J].PhysicalReviewB，2002，65:172510.

[14]J.J.ZhaoandJ.P.Lu.Pressure-inducedmetallizationinsolidboron[J].PhysicalReviewB，2002，66:092101.

[15]C.Y.He，C.X.Gao，Y.Z.Ma，M.Li，A.M.Hao，X.W.Huang，B.G.Liu，D.M.Zhang，C.L.Yu，G.T.Zou，Y.C.Li，H.Li，X.D.Li，andJ.Liu.Insituelectricalimpedancespectroscopyunderhighpressureondiamondanvilcell[J].AppliedPhysicsLetter，2007，91:092124.

[16]M.K.Kazimierczuk，G.Sancineto，G.Grandi，U.Reggiani，andA.Massarini.IEEETrans[J].Magn，1999，35:4185.

[17]H.C.Hamaker.TheLondon-vanderWallsattractionbetweensphericalparticles[J].Physica.1937，4(10):1058-1072.

[18]F.London.Thegeneraltheoryofmolecularforces[J].TransactionsoftheFaradaySociety，1937，33:8b.

[19]M.M.BülbülandS.Zeyrek.Frequencydependentcapacitanceandconductance-voltagecharacteristicsofAl/Si3N4/p-Si(100)MISdiodes[J].MicroelectronicEngineering，2006，83(11-12):2522-2526.