橋梁阻尼測試與分析方法研究

劉漢夫

(中國鐵道科學研究院鐵道建筑研究所，北京 100081)

橋梁阻尼測試與分析方法研究

劉漢夫

(中國鐵道科學研究院鐵道建筑研究所，北京 100081)

研究了兩種橋梁阻尼特性系數的測試與分析方法，說明了各自方法的特點和適用條件，導出了兩者的轉換關系。著重討論了頻率分辨率對阻尼比系數的精度影響，通過實例提出了阻尼比系數的精度判別標準。

對數衰減阻尼 阻尼比 功率譜密度 頻率分辨率 采樣量 分析點數

作為結構特性之一，結構阻尼的測試和分析一直受到工程界的重視。如果說結構的其它固有特性，例如結構自振頻率、振型等，還可以通過結構計算得到，則結構的阻尼卻只有通過實測才能得到。在很多考慮阻尼的結構動力響應分析中，缺乏完備準確的結構阻尼實測資料是導致分析與實測結果誤差加大的一個重要原因。

在橋梁結構阻尼的測試方面，也有很多亟待解決和澄清的問題，比如有的測試結果給出的是“對數衰減阻尼系數”，而有的給出的是“阻尼比系數”，這兩者之間有什么關系，每種方法有什么樣的適用條件以及如何保證阻尼分析結果的足夠精確等等。應該看到:僅僅得到一個結果遠遠不是試驗的目的，問題的關鍵是試驗者還必須能夠證明試驗結果的正確和有效。只有做到這一點，測試結果才是成功的、有意義的。

1 兩種阻尼特性系數的方法分析

1.1 對數衰減阻尼

《鐵路橋梁檢定規范》(1978年舊版及2004年新版)規定的就是這種方法，它是利用橋梁振動的衰減曲線，采取振幅按對數的衰減來代表橋梁的全部阻尼，參見圖1。

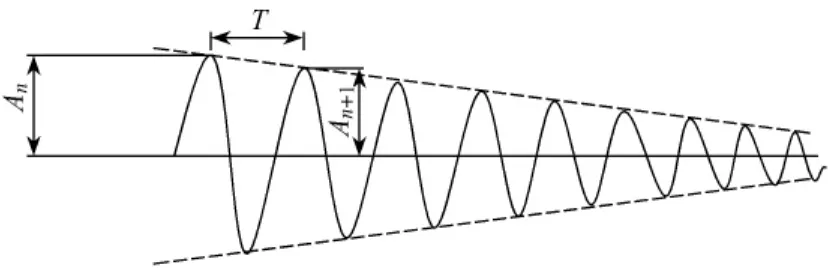
圖1 橋梁振動的衰減曲線示意

對數衰減阻尼系數γ定義為

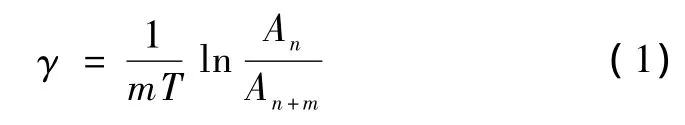
式中，γ為m個振動周期上的對數衰減阻尼系數平均值; m為振動周期的個數;T為單個振動周期的時間;An為第n個波幅的單振幅;An+m為第n+m個波幅的單振幅。

1.2 根據半功率帶寬法得到的阻尼比系數ξ

ξ在動力學上稱之為相對阻尼系數。對如圖2這樣一個振動系統的幅頻響應曲線，c為系統共振頻率響應點，a、b為半功率點，反映在幅頻曲線上即是共振頻率f0對應幅值y0的0.707倍處的兩個點。根據幅頻曲線的有關分析可以證明阻尼比

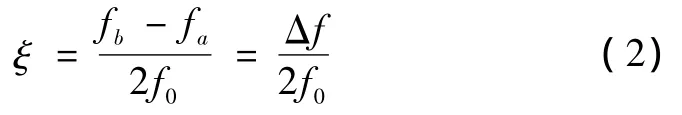
式中fa，fb及f0的意義見圖2。

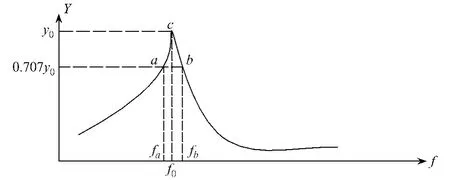
圖2 利用幅頻曲線分析阻尼比示意

1.3 對數衰減阻尼系數γ與阻尼比系數ξ的關系

對這兩種從不同側面反映系統阻尼的物理量，籠統地冠以所謂“阻尼系數”是不夠嚴密的。其實，它們均有不同的適用場合，也有一定的轉換關系，現以單自由度系統的振動推導它們的關系。

有阻尼單自由度系統振動微分方程的一般形式為

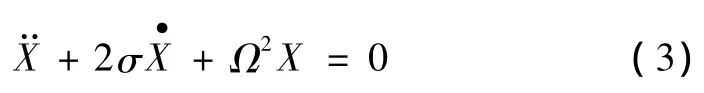
式中，σ為振動衰減系數，是阻尼效果的一種表達形式，可以證明，σ與相對阻尼系數ξ的關系為:σ=ξΩ; Ω為單自由系統無阻尼自由振動的固有圓頻率。

方程(3)中的振動衰減系數σ實際上就是對數衰減阻尼系數γ，證明如下。微分方程(3)的通解為

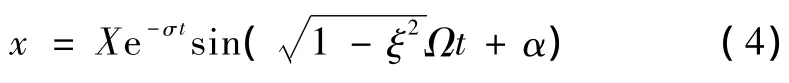
假定t=t1時波幅達到第n個峰值An;在t=t1+mT(T為衰減振動的周期)時波幅達到第n+m個峰值An+m，則:An/An+m=Xe－σt1/Xe－σ(t1+mT)=eσmT

由此可得

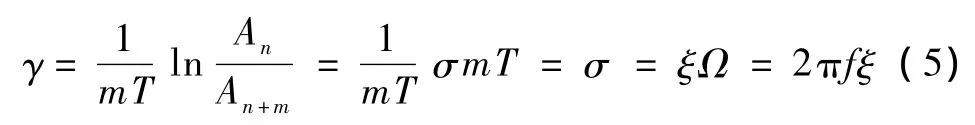
式(5)即為結構振動的對數衰減阻尼系數γ與阻尼比系數ξ之間的關系式。應該注意γ的量綱是rad/s，而ξ是個無量綱的值。

2 兩種阻尼特性系數的正確應用

2.1 對數衰減阻尼系數γ

從以上分析可以看出，對數衰減阻尼是一種較初級，而且簡單易行的分析方法。在20世紀70年代末，由于頻譜分析技術在我國鐵路橋梁測試界應用得還不很成熟，所以被當時的《鐵路橋梁檢定規范》所采納。該方法細致分析起來尚有很大的局限性。

1)嚴格地說，阻尼應該是針對某種振型的阻尼才有意義。對數衰減阻尼往往只是根據一個點的振動測試結果得出，無法判斷實際發生的振型，這樣的數據應用到理論分析中會造成很大的不便。

2)對于稍復雜一些的結構，由于實際結構上某一點的振動往往是多種振型的疊加，必須采用模態分析的方法，把各種振型分離開來，對每種單獨的振型分析阻尼才有意義。

3)從理論上說，對數衰減阻尼分析法只適用于實際上只有一種振型出現的簡單結構，比如跨度比較短的簡支結構。一般來說，列車余振條件下，這種結構出現的多是唯一的一階撓曲振型，這時可以用對數衰減阻尼法來分析結構在該振型條件下的阻尼，并根據式(5)得到理論分析中最感興趣的ξ值。

值得注意的是，ξ值一般是根據結構脈動試驗分析而得，它體現的是結構在微振動條件下的結構阻尼情況，某種振型條件下的ξ值應該是個不變量。而γ值是根據橋梁結構的強迫激勵后的衰減振動分析而得，體現的是結構在較大幅值振動條件下的阻尼。由于實際結構的約束是與其變形的大小相關的，因此實際上結構的阻尼特性也與其變形的強弱相關，所以在不同振幅衰減條件下γ值有可能表現的不是一個常值。理論上說，只有微小衰減振動條件下所得的γ值，才可以根據式(5)換算到ξ值。

4)理論分析中往往關心結構在多種振型條件下的阻尼系數ξ值，顯然對數衰減阻尼分析法是不能完成這項工作的。

2.2 根據半功率帶寬法得到的阻尼比系數ξ值

這種方法無疑比對數衰減阻尼法前進了一大步，但是，在應用的過程中牽涉到許多模態分析識別和ξ值分析精度的認證技術。應用得好，會給理論分析者提供相當準確的各模態條件下的阻尼比ξ值;反之，應用不當會造成分析結果的重大偏差。

根據式(2)，影響ξ值的量有兩個:半功率點的帶寬Δf與系統的共振頻率值f0，而這兩個量的精度是與譜分析過程中的頻率分辨率Δfs相關的。應該說頻率分辨率Δfs越高，即譜線間隔越密ξ值的精度就越高。當Δfs取值達到足夠小的時候，ξ值應該趨于穩定。

提高頻率分辨率的途徑有兩個:其一是在數據采樣時采用較低的采樣頻率，對于大型低頻結構采樣前可以通過加低通模擬濾波器的方法使采樣頻率降低下來。其二是加長數據的分析點數，最好在采樣時采樣量要達到幾十k甚至更長的數據量。分析時利用一些成熟的分析軟件進行FFT分析，至于一次FFT分析是使用部分數據還是使用全部數據，要看ξ的計算值是否達到穩定。理論上說，只有ξ值達到穩定，才有理由認為阻尼的測試與分析是成功的、可信的。

根據文獻［1］，當Δf≥2Δfs時，ξ計算值接近穩定，這可以說是判別ξ值精度的一個粗略標準，究竟ξ值的分析精度是否達到要求，尚需根據前后兩次不同分析點數的FFT分析結果來判定。

3 分析實例——頻率分辨率對ξ值的影響

3.1 汕頭海灣大橋測試簡介

汕頭海灣大橋全長2 500 m，其中主橋為長760 m的懸索結構，采用54 m+452 m+154 m三跨雙鉸預應力混凝土加勁箱梁結構體系，主纜間距5.7 m。在主橋的自振特性脈動試驗過程中，測試系統參數設置如下:

1)由于測試的目的是得到無阻尼自由振動條件下結構的固有頻率，而位移、速度和加速度三者只有速度的共振頻率等于系統的無阻尼自振頻率，因此試驗中拾取的必須是速度信號;

2)低通濾波器的截止頻率設置為10 Hz;

3)采樣頻率設置為40 Hz;

4)每點采樣數據量控制在30 k左右。

3.2 豎向某階模態振型ξ值的測試與分析示例

現僅以主橋中跨中上游的豎向振動為例說明問題，試驗中通過測試系統衰減檔的控制，把速度信號的最大單向電壓量響應值控制在－3～+3(V)范圍內。

從1～1 024數據點的功率譜密度分析可以粗略地看出:振動成份主要集中在0.24～4.15 Hz的頻帶上。如果僅從1～1 024點的譜密度分析上看，譜密度最大值落于2.495 Hz頻點處，見圖3至圖6及表1。當然，該頻率點處的橋梁振型可以根據多點的自譜與互譜分析得到。現要著重說明的是，在各種不同的分析處理模式下，該頻率點及ξ值的變化規律。

根據以上分析可得結論如下:

1)影響ξ值的主要因素是譜分析過程中的頻率分辨率Δfs，在本例中得以反映的就是:在Δfs值小于0.003 906 Hz時(分析點數達到10 240以上時)，ξ值才趨于穩定。

2)傳統的1 024點譜分析，由于分析點數的限制，很難確保阻尼分析中的足夠頻率分辨率，僅僅根據1 024點的1次或多次平均譜分析，ξ值的計算精度將嚴重不足。

3)從圖3、圖4的對比上看，在大型結構的脈動試驗譜分析過程中，對于幾十k甚至更長的實驗數據記錄，如果僅僅是采用1 024點多次平均計算，只會對譜峰的高低對比有影響，對提高ξ值的計算精度效果不佳。

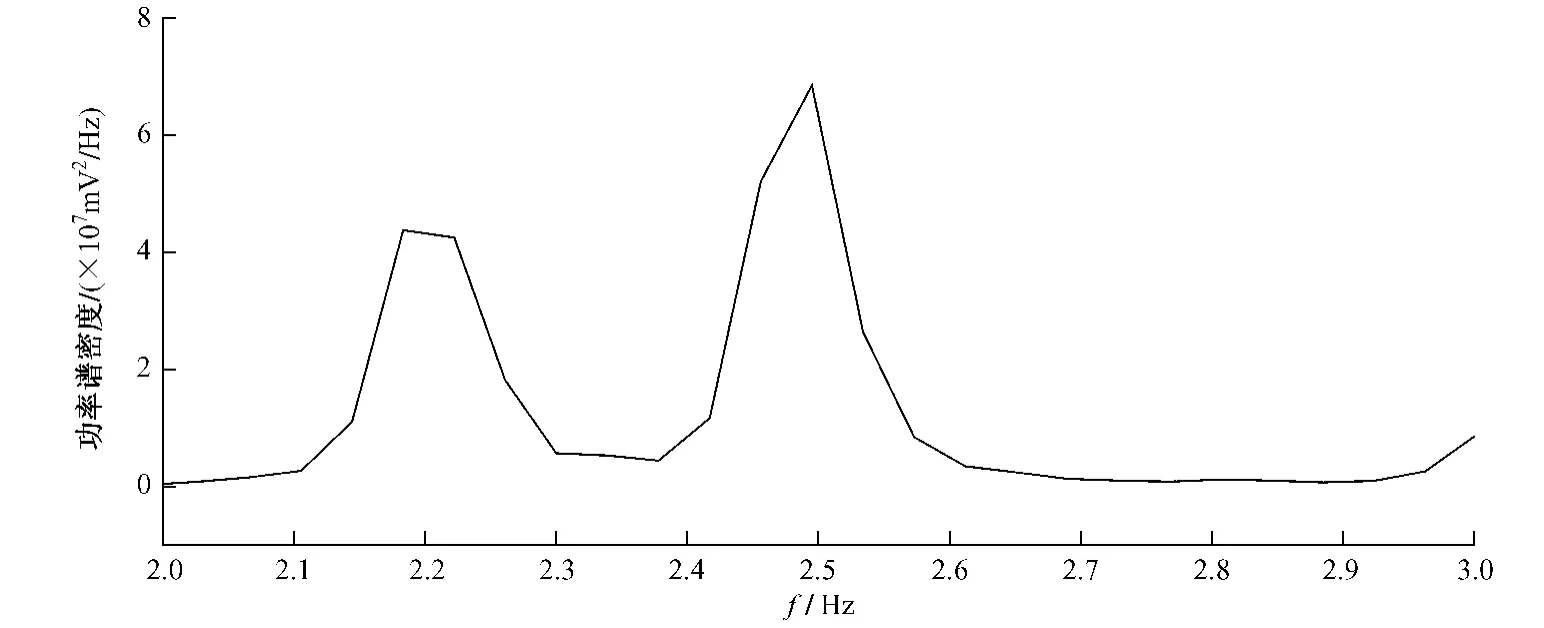
圖3 1～1 024數據點功率譜密度(平均次數1)局部展開圖

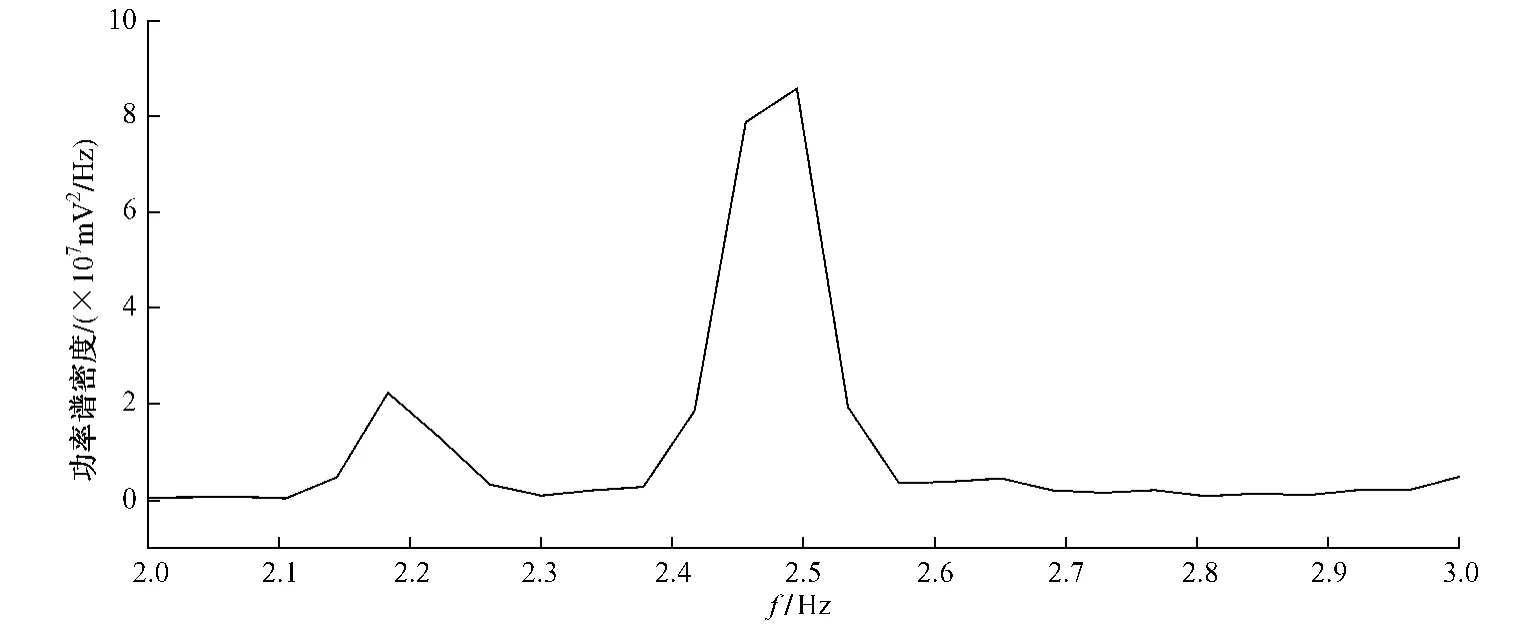
圖4 1024數據點功率譜密度(平均次數10)局部展開圖

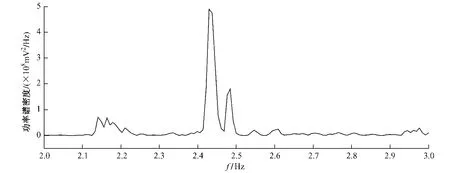
圖5 1～5 120數據點功率譜密度(平均次數1)局部展開圖

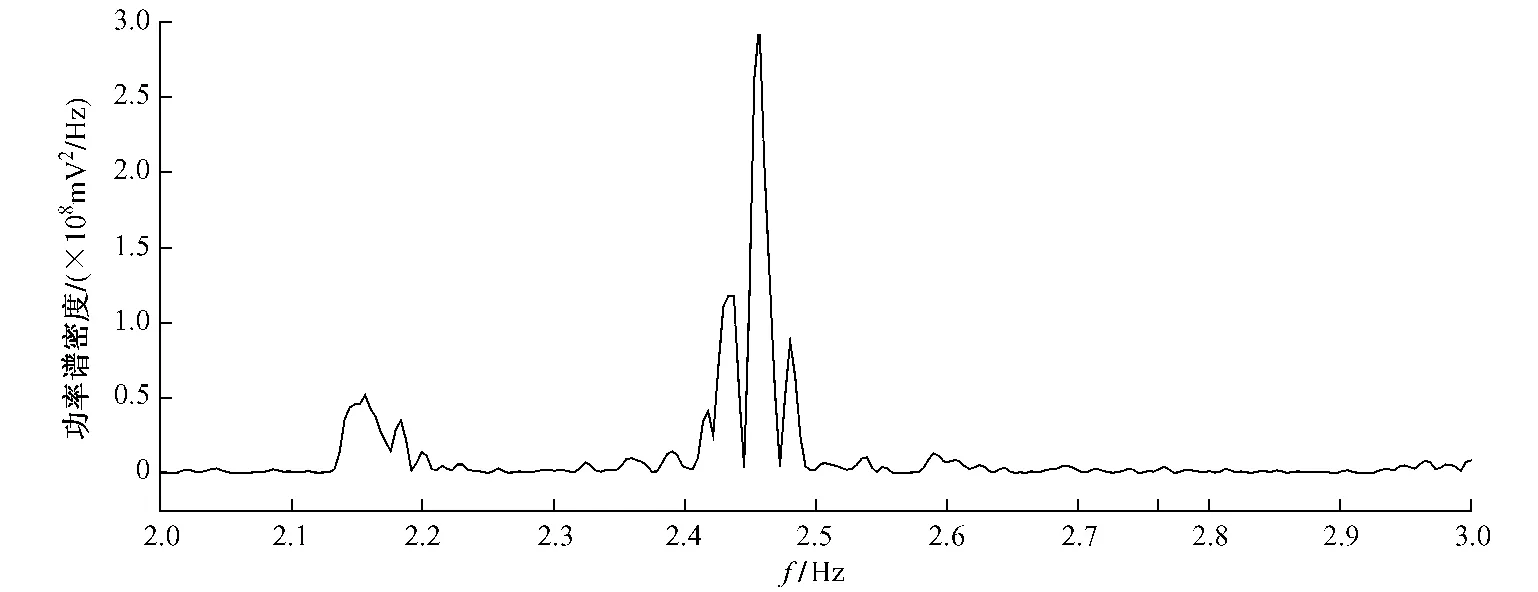
圖6 1～10 240數據點功率譜密度(平均次數1)局部展開圖

表1 不同分析方法ξ值的計算結果

4)隨著Δfs值的細化和深入，由于0～奈氏頻率間譜線條數的增加，相距很近的各頻率成份將被區分開來，這使得頻率成份的認定在不同的Δfs值下會有一定的誤差，由于Δfs是在很小的基礎上繼續細化，使得這種頻率上的誤差在數量上不是很顯著，這可以從圖5、圖6中看得很清楚。但是，Δfs的繼續細化對ξ值的影響卻是巨大的，直至Δfs值達到某一限度以后，ξ值的結果趨于穩定，這時可以認為ξ值的精度合格，接近于真實值。

5)計算分析結果表明:ξ值的精度是否合格，關鍵是要控制Δfs值，使得半功率點的頻帶寬度Δf內的譜線數要足夠多。該例分析表明:當Δf≥3Δfs時，ξ值的結果趨于穩定。

4 結語

1)對數衰減阻尼系數γ的測試與分析方法，作為一種在20世紀70年代以前我國鐵路橋梁檢測界使用的方法，已經明顯地暴露出其使用上的局限性，它只適用于那些結構簡單、衰減振動振型簡單明確的結構。

2)基于頻譜分析的半功率帶寬法求解阻尼比系數ξ，是根據結構脈動試驗結果，分析結構在各振型下阻尼的一種廣泛意義上的方法，它適用于各種大型低頻結構的阻尼分析。

3)本文基于有阻尼的單自由系統振動微分方程推導出γ與ξ的關系:γ=2πfξ。

4)ξ值在分析計算過程中的精度主要由頻率分辨率Δfs控制，本文實例分析結果證明:只有當半功率帶寬Δf≥3Δfs時，ξ值的結果才趨于穩定，這可以說是阻尼分析精度的一個判別條件。實例分析還證明:傳統的1 024點1次或多次平均譜分析的方法不能滿足該判別條件，用該方法分析得到的阻尼比系數不可靠。

5)為得到有意義的結構阻尼，在數據的采樣時必須注意三點:其一是在使用低通抗混濾波器的前提下，根據情況盡可能使用較低的采樣頻率;其二是合理地控制信號的強弱，信號的單向電壓量最好控制在1.0 V以上;其三根據現場情況盡可能地加大數據采樣量，使得分析阻尼時可以獲得足夠的頻率分辨率。

6)現代的頻譜分析儀，一般都不同程度地設有1 024～4 096點的譜分析方法，在ξ值的分析中，關鍵是要增加每一次譜分析的數據點，因此要打破1 024～4 096點譜分析的限制，利用其它譜分析軟件，采用更長的數據分析才能保證阻尼分析結果的可靠。

［1］應懷樵.大型低頻結構半功率帶寬法高精度求阻尼比的研究［C］∥第六屆全國振動理論及應用會議論文，北京:航空工業出版社，1996.

［2］李德葆.振動模態分析及其應用［M］.北京:宇航出版社，1989.

［3］中華人民共和國鐵道部.鐵運函［2004］120號鐵路橋梁檢定規范［S］.北京:中國鐵道出版社，2004.

［4］中華人民共和國鐵道部.［1977］電字1279號鐵路橋梁檢定規范［S］.北京:人民鐵道出版社，1978.

U446

A

1003-1995(2011)02-0007-04

2010-09-15;

2010-11-10

劉漢夫(1964—)，男，遼寧本溪人，副研究員，碩士。

(責任審編 趙其文)