基于DPSO的不確定系統測試性建模*

王成剛，應朝龍，李建海，劉志遠

1.海軍航空工程學院 基礎實驗部， 山東 煙臺264001；

2.濟南軍區軍械雷達修理所， 濟南250022

關聯模型也稱為推理模型，表示的是部件之間的因果關系，是目前測試性分析中普遍采用的一種建模技術。但是，復雜裝備常存在故障與測試之間關聯關系不清楚的現象。而從裝備使用階段實際測試性分析與評估的角度來說，由于復雜系統的結構和部件間關系復雜，實際測試性評估往往是小樣本下的基于不確定信息的評價決策問題[1]。由于這些模型不具備對不確定信息的處理能力，因此對實際測試性評估的結果可信度不高，所以必須研究新的測試性分析與評估方法。文獻[ 2]針對航天器中依賴關系不確定的系統，提出采用概率描述不確定系統多信號模型的依賴矩陣，并采用貝葉斯網絡的參數學習和結構學習算法來建立不確定系統的多信號模型因果依賴關系和概率依賴矩陣。文獻[ 3]提出了基于貝葉斯網絡的測試性預計方法。文獻[ 4]將測試時間引入貝葉斯網絡(Bayesian Networks，BN)，使基于貝葉斯網絡的測試性評估與故障檢測與隔離時間相關，從而既考慮了系統的不確定信息，又能夠得到系統的FDT和FIT。本文利用離散粒子群算法，實現貝葉斯網絡結構學習。

1 基于BN的不確定系統測試性建模

1.1 基于BN的測試性模型

采用BN來表達故障模式和測試之間的關聯關系，稱為測試性評估BN模型。測試性BN模型包括兩個層次的節點：一是由故障模式節點組成的層次；二是由測試信號節點組成的層次。同層次的節點間沒有關聯關系，關聯關系只能存在于不同層次的節點間[4]。

可用一個五元組＜F， Te， D， P， Tt＞表達測試性BN模型，如圖1所示，其中

F={F0， F1， F2， …Fn}是故 障模式節點 集， F0表示無故障；

Te={te1， te2， …tem}是測試節點集；

D是連接節點的有向邊集；

P是網絡中的條件概率集；

Tt={t1， t2， …tm}是網絡中的測試時間集。

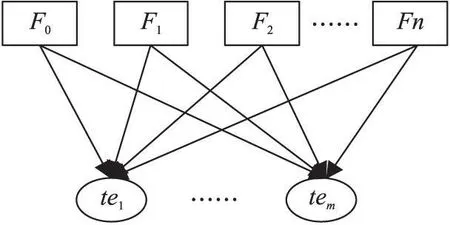
圖1 測試性BN模型示意圖

測試性評估BN模型可以采取兩種方式建立：一是按因果方向建模，用輸入節點表達故障模式，用輸出節點表達測試信號；二是按測試方向建模，用輸入節點表達測試信號，用輸出節點表達故障模式。

1.2 基于BN的測試性建模流程

BN建造的一般流程可以用圖2表示。由圖可見， BN建造首先是一個故障分析過程，獲得設備故障模式及其相關信息，其次是建立節點之間的依賴關系和節點的條件概率估計。

圖2 測試性BN建模流程圖

隨著維修測試數據的積累， 往往會需要增加(或減少)新的節點變量或需要調整網絡的結構，此時，需要根據需要對貝葉斯網絡結構重新學習。貝葉斯網絡可以自動完成這個學習過程，根據學習結果改變網絡的結構(節點增減、連接更改)和參數。

另外，在基于統計數據的測試性BN建模過程中，由于故障征兆與故障原因統計的不完全性，致使測試性BN結構學習屬于數據不完備情況下的參數和結構學習問題。

1.3 測試性數據完備化

由于一個元件的故障可能出現多個征兆(影響到幾個功能)，而實際測試中各故障征兆的觀測有時是不完備的，文獻[5]中貝葉斯網絡沒有考慮征兆層之間的關聯關系。本文考慮了測試信號之間的關聯關系，利用測試—測試關聯矩陣對觀測數據進行完備化處理。將不確定系統測試性分析由原來的數據不完備情況下的貝葉斯網絡結構和參數學習問題轉化為數據完備情況下的貝葉斯網絡結構和參數學習問題。

將測試—測試關聯矩陣記為TT=[ ttij] ，描述測試間的因果邏輯關系[6]。若ti輸出異常時， tj輸出必然異常，則ttij=1；否則， ttij=0。

利用測試—測試關聯矩陣，在故障—測試樣本數據中，測試ti輸出異常時，若tj數據缺失，則可根據矩陣TT=[ttij]將數據補齊。

1.4 測試性建模參數學習

測試性BN結構學習就是要尋找一種網絡，能按某種目標函數最好地與給定故障數據樣本擬合。目標函數用來衡量測試性評估BN表達數據樣本的準確度。假設數據樣本沒有丟失數據，數據是完整的，同時獨立且同分布，目標函數可構造為[7]

為了表示測試性評估BN的條件獨立性，根據BN條件獨立的依賴關系，可對目標函數進行分解，即式(1)分解為關于每個測試與所有故障的獨立因式

其中， Nij表示數據中事件πVi=發生的次數。 ˉθij是事 件 πVi=發生的最大概率值，等于表示Vi有可能取值的個數。

2 基于DPSO的BN結構學習

式(2)是高維非線性函數，可用PSO算法求解。PSO算法中的粒子跟蹤個體和全局極值，在整個問題空間中流動， 以尋求最優解[8-9]。另一方面，式(2)適應度函數是個離散的優化問題。因此，當將PSO算法應用于貝葉斯網絡結構學習時，對應的粒子是貝葉斯網絡的結構(矩陣)，而該結構為二進制編碼，只能采用離散粒子群(Discrete Particle Swarm Optimization， DPSO)算法[10]。

2.1 位置及編碼方式

由于BN結構學習的結果是一個與訓練數據匹配較好的網絡結構，因此可以認為每一種粒子位置狀態對應一個網絡結構，狀態空間是所有可能結構的集合。對于測試性BN結構的編碼，可將網絡中每一個變量的編碼用其父節點集合來表示[9]。整個網絡的編碼就是按一定順序排列的節點的父節點集合。例如，編碼為[te1|f0， f1， …， fm；te2|f0， f1， …， fm；…；ten|f0， f1， …， fm]，用分號來把各父節點集分開。“|”前邊是要表示的節點(信號、功能或測試)， “|”后邊是該節點的父節點集(故障)。每個節點的局部結構(該節點和其父節點集)都可以表示成位置的一個分量的形式。若fi和tej關聯，則相應的編碼位為1；否則為0。

2.2 DPSO

1997年Kennedy和Eberhart提出了DPSO，他們在提出的模型中將每一維和限制為1 或者為0，而速度不作這種限制[11]。用速度表示位置狀態改變的可能性，用速度來更新位置時，如果值大一些，粒子的位置更有可能為1，值小一點則可能為0。速度既然是一個概率值，那么它應該限制在[ 0， 1]之間，由Sig()函數實現， DPSO所定義的粒子速度更新公式和位置公式如下

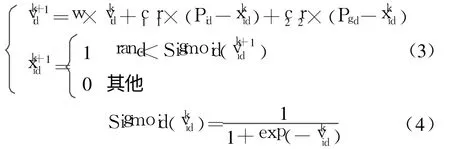
其中， rand是[0， 1]之間的隨機數，算法中的其他參數都和基本粒子群算法的參數相同。式(3)可表達如下：

Xj=w×Xj⊕c1r1(Xjp⊙Xj)⊕c2r2(Xg⊙Xj)(5)

其中， Xi=Z(x1， …， xq)， i=1， …， K，稱為編碼粒子，共有K個，其中， Z為編碼算子。 Xjp為第j編碼粒子所經歷的最好編碼；Xg表示所有編碼粒子所經歷的最好編碼。

⊙法則定義為X1⊙X2是編碼粒子X1和X2的交叉變換。

⊕法則定義為各交叉變換的連接序列。

×法則定義為編碼粒子的自交換。

w是編碼位自交換的隨機位置， c1r1、c2r2是編碼位的交叉變換的隨機位置。

式(5)的含義是：當前編碼粒子進行自交換，由自身的改變得到新的編碼粒子；然后與個體極值作隨機的交叉操作，產生含有個體極值編碼的新編碼；再與全局極值作隨機的交叉操作，又具有了全局極值部分。

3 實例分析

以文獻[12]中電路為例，某基地級修理廠的故障維修數據如表1 所示。基于該組數據，利用本文算法建立該電路基于BN的測試性模型，得到關聯矩陣；再利用采樣統計求得條件概率，將二者合并后得到關聯概率矩陣，如表2所示。

表1 某基地級修理廠故障維修數據

表2 關聯概率矩陣

由上表可以得到測試的FDR、FIR和FIR。與文獻[ 4]中方法相比，本文方法考慮了測試信號樣本數據的不完備性及測試的不確定性，利用測試—測試關聯矩陣對樣本數據進行了完備化處理，當數據缺失時，測試性分析中的關聯概率矩陣更加貼近實際水平。

4 結論

在基于統計數據的測試性建模與評估中，由于故障征兆與故障原因統計的不完全性，致使測試性評估BN結構學習屬于數據不完備情況下的結構和參數學習問題，針對該問題利用離散粒子群算法，通過測試數據完備化，以貝葉斯測度為計分值，實現了貝葉斯網絡結構學習，從而完成了不確定系統的測試性建模。

[ 1] 王波，姜新軍，孟上.一種求解D-S診斷識別框架方法[ J] .海軍航空工程學院學報， 2008， 23(4)：445-448.

[ 2] 龍兵.多信號建模與故障診斷方法及其在航天器中的應用研究[D].哈爾濱：哈爾濱工業大學， 2005.

[ 3] 徐赫，王寶龍， 武建輝.基于貝葉斯網絡的測試性預計方法[ J] .彈箭與制導學報， 2007， 27(4)：232-235， 239.

[ 4] 王成剛，周曉東，王學偉.基于貝葉斯網絡的復雜裝備測試性評估[ J] .電子測量與儀器學報， 2009， 23(5)：17-21.

[ 5] 連光耀.基于信息模型的復雜電子裝備測試性設計與分析方法研究[ D] .石家莊：軍械工程學院， 2008.

[ 6] 楊鵬，邱靜，劉冠軍.基于擴展的關聯模型的測試性分析技術研究[ J] .系統工程與電子技術， 2008， 30(2)：371-374.

[ 7] 劉大有，王飛.基于遺傳算法的Bayesian網結構學習研究[ J].計算機研究與發展， 2001， 38(8)：916-922.

[ 8] 王波，吳華麗，王燦林.基于貝葉斯網絡的復雜裝備D-S診斷[ J] .計算機仿真， 2009， 28(4)：34-37.

[ 9] 劉欣，賈海洋，劉大有.基于粒子群優化算法的Bayesian網絡結 構 學 習[ J].小型微型計算機系統， 2008， 29(8)：1516-1519.

[ 10] Elon SCorrea， Alex A Freitas， Colin G Johnson.Particle Swarm for Attribute Selection in Bayesian Classification：An Application to Protein Function Prediction[ J] .Journal of ArtificialEvolution and Applications， 2008， 1-12.

[ 11] EberhartR C， Kennedy J.ADiscrete Binary Version of the Partic le Swarm Algorithm[ C] //IEEE Conference on Systems， Man，and Cybernetics， Orlando， FL， 1997：4104-4109.

[ 12] 王成剛，周曉東，王學偉.面向ATE的電路板測試性分析及評估方法研究[ J] .電子器件， 2008， 31(5)：1599-1602.王成剛(1976-)， 男，工 程師， 博士， 主要研究方向為智能制導、測試性分析與評估。